leetcode weekly contes 358 最近周赛状态一直不稳定,感觉还是智商不够,遇到非常难的题目就手速很慢了,只适合左板子题目和简单题目练手速,当然越来越不喜欢手速题目,还是喜欢思考的题目,上周的比赛失误太严重。
6939. 数组中的最大数对和 给你一个下标从 0 开始的整数数组 nums 。请你从 nums 中找出和 最大 的一对数,且这两个数数位上最大的数字相等。
返回最大和,如果不存在满足题意的数字对,返回 -1 。
示例 1:
输入:nums = [51,71,17,24,42] 输出:88 解释: i = 1 和 j = 2 ,nums[i] 和 nums[j] 数位上最大的数字相等,且这一对的总和 71 + 17 = 88 。 i = 3 和 j = 4 ,nums[i] 和 nums[j] 数位上最大的数字相等,且这一对的总和 24 + 42 = 66 。 可以证明不存在其他数对满足数位上最大的数字相等,所以答案是 88 。
示例 2:
输入:nums = [1,2,3,4] 输出:-1 解释:不存在数对满足数位上最大的数字相等。
提示:
2 <= nums.length <= 1001 <= nums[i] <= 104
地址 https://leetcode.cn/contest/weekly-contest-358/problems/max-pair-sum-in-an-array/
题意 直接模拟
思路
找到每个数字上最大的位数即可,找到相同的即可,可以优化到 $O(n\log U)$。
复杂度分析:
时间复杂度:$O(n \log U)$, 其中 $n$ 表示数组的长度,$U$ 表示数组中的最大值。
空间复杂度:$O(\log U)$。
代码 [sol1-C++] class Solution {public : int maxSum (vector<int >& nums) int n = nums.size (); int res = -1 ; for (int i = 0 ; i < n; i++) { for (int j = i + 1 ; j < n; j++) { string s1 = to_string (nums[i]); string s2 = to_string (nums[j]); sort (s1.begin (), s1.end ()); sort (s2.begin (), s2.end ()); if (s1.back () == s2.back ()) { res = max (res, nums[i] + nums[j]); } } } return res; } };
6914. 翻倍以链表形式表示的数字 给你一个 非空 链表的头节点 head ,表示一个不含前导零的非负数整数。
将链表 翻倍 后,返回头节点 head 。
示例 1:
输入:head = [1,8,9] 输出:[3,7,8] 解释:上图中给出的链表,表示数字 189 。返回的链表表示数字 189 * 2 = 378 。
示例 2:
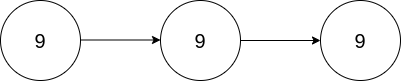
输入:head = [9,9,9] 输出:[1,9,9,8] 解释:上图中给出的链表,表示数字 999 。返回的链表表示数字 999 * 2 = 1998 。
提示:
链表中节点的数目在范围 [1, 104] 内
0 <= Node.val <= 9生成的输入满足:链表表示一个不含前导零的数字,除了数字 0 本身。
地址 https://leetcode.cn/contest/weekly-contest-358/problems/double-a-number-represented-as-a-linked-list/
题意 直接模拟
思路
本质上是大数乘法,最简单的做法时将链表转换为数字,然后直接在数字上做大数乘法,比计算进位等,然后将乘法的结果再返回构成链表返回即可,主要是用 c++ 刷题不占优势,不如 python 选手手速快。
复杂度分析:
时间复杂度:$O(n)$,其中 $n$ 为链表的长度。
空间复杂度:$O(n)$,其中 $n$ 为链表的长度。
代码 class Solution {public : ListNode* doubleIt (ListNode* head) { vector<int > arr; while (head) { arr.emplace_back (head->val); head = head->next; } reverse (arr.begin (), arr.end ()); int carry = 0 ; for (int i = 0 ; i < arr.size (); i++) { int curr = (arr[i] * 2 + carry) / 10 ; arr[i] = (arr[i] * 2 + carry) % 10 ; carry = curr; } if (carry > 0 ) { arr.emplace_back (carry); } reverse (arr.begin (), arr.end ()); ListNode *res = nullptr ; ListNode *cur = nullptr ; for (int i = 0 ; i < arr.size (); i++) { ListNode *node = new ListNode (arr[i]); if (!cur) { res = node; cur = node; } else { cur->next = node; cur = cur->next; } } return res; } };
7022. 限制条件下元素之间的最小绝对差 给你一个下标从 0 开始的整数数组 nums 和一个整数 x 。
请你找到数组中下标距离至少为 x 的两个元素的 差值绝对值 的 最小值 。
换言之,请你找到两个下标 i 和 j ,满足 abs(i - j) >= x 且 abs(nums[i] - nums[j]) 的值最小。
请你返回一个整数,表示下标距离至少为 x 的两个元素之间的差值绝对值的 最小值 。
示例 1:
输入:nums = [4,3,2,4], x = 2 输出:0 解释:我们选择 nums[0] = 4 和 nums[3] = 4 。 它们下标距离满足至少为 2 ,差值绝对值为最小值 0 。 0 是最优解。
示例 2:
输入:nums = [5,3,2,10,15], x = 1 输出:1 解释:我们选择 nums[1] = 3 和 nums[2] = 2 。 它们下标距离满足至少为 1 ,差值绝对值为最小值 1 。 1 是最优解。
示例 3:
输入:nums = [1,2,3,4], x = 3 输出:3 解释:我们选择 nums[0] = 1 和 nums[3] = 4 。 它们下标距离满足至少为 3 ,差值绝对值为最小值 3 。 3 是最优解。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1090 <= x < nums.length
地址 https://leetcode.cn/contest/weekly-contest-358/problems/minimum-absolute-difference-between-elements-with-constraint/
题意
二分查找
思路
力扣上经典的板子题目了,已经遇多次了,假设当前遍历的元素索引为 $i$,此时我们可以用$treeset$ 保存区间 $[0,i-x]$ 之间的元素,每次要找距离 $nums[i]$ 最近的元素时,此时直接直到最小的大于等于 $nums[i]$ 的元素 $x$,已经最大的小于等于 $nums[i]$ 的元素 $y$, 此时距离 $nums[i]$ 最近的元素则在 $(x,y)$ 中选择其一了,可以利用 $treeset$ 的特性即可。
复杂度分析:
时间复杂度:$O(n \log n)$,其中 $n$ 表示数组的长度。
空间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
代码 class Solution {public : int minAbsoluteDifference (vector<int >& nums, int x) set<int > cnt; int res = INT_MAX; int n = nums.size (); for (int i = 0 , j = 0 ; i < n; i++) { if (i - j >= x) { cnt.emplace (nums[j++]); auto it = cnt.lower_bound (nums[i]); if (it != cnt.end ()) { res = min (res, abs (*it - nums[i])); } if (it != cnt.begin ()) { it--; res = min (res, abs (*it - nums[i])); } } } return res; } };
7023. 操作使得分最大 给你一个长度为 n 的正整数数组 nums 和一个整数 k 。
一开始,你的分数为 1 。你可以进行以下操作至多 k 次,目标是使你的分数最大:
选择一个之前没有选过的 非空 子数组 nums[l, ..., r] 。
从 nums[l, ..., r] 里面选择一个 质数分数 最高的元素 x 。如果多个元素质数分数相同且最高,选择下标最小的一个。
将你的分数乘以 x 。
nums[l, ..., r] 表示 nums 中起始下标为 l ,结束下标为 r 的子数组,两个端点都包含。
一个整数的 质数分数 等于 x 不同质因子的数目。比方说, 300 的质数分数为 3 ,因为 300 = 2 * 2 * 3 * 5 * 5 。
请你返回进行至多 k 次操作后,可以得到的 最大分数 。
由于答案可能很大,请你将结果对 109 + 7 取余后返回。
示例 1:
输入:nums = [8,3,9,3,8], k = 2 输出:81 解释:进行以下操作可以得到分数 81 : - 选择子数组 nums[2, ..., 2] 。nums[2] 是子数组中唯一的元素。所以我们将分数乘以 nums[2] ,分数变为 1 * 9 = 9 。 - 选择子数组 nums[2, ..., 3] 。nums[2] 和 nums[3] 质数分数都为 1 ,但是 nums[2] 下标更小。所以我们将分数乘以 nums[2] ,分数变为 9 * 9 = 81 。 81 是可以得到的最高得分。
示例 2:
输入:nums = [19,12,14,6,10,18], k = 3 输出:4788 解释:进行以下操作可以得到分数 4788 : - 选择子数组 nums[0, ..., 0] 。nums[0] 是子数组中唯一的元素。所以我们将分数乘以 nums[0] ,分数变为 1 * 19 = 19 。 - 选择子数组 nums[5, ..., 5] 。nums[5] 是子数组中唯一的元素。所以我们将分数乘以 nums[5] ,分数变为 19 * 18 = 342 。 - 选择子数组 nums[2, ..., 3] 。nums[2] 和 nums[3] 质数分数都为 2,但是 nums[2] 下标更小。所以我们将分数乘以 nums[2] ,分数变为 342 * 14 = 4788 。 4788 是可以得到的最高的分。
提示:
1 <= nums.length == n <= 1051 <= nums[i] <= 1051 <= k <= min(n * (n + 1) / 2, 109)
地址 https://leetcode.cn/contest/weekly-contest-358/problems/apply-operations-to-maximize-score/
题意
素数筛选 + 单调栈 + 幂乘法 + 贪心
思路
首先题目意思是给定的 $[l,r]$ 选择质数分数最大的元素,对于选择策略来说需要考虑如下:
若想得到最大的分数,此时我们应该尽可能的选择数组中最大的元素;
假设数组中最大的元素为 $nums[i]$, 由于每次选择的子数组不可能相同,那么需要思考一下 $nums[i]$ 最多可以选多少次,即所有以 $nums[i]$ 为质数分数的最大元素可以构成的不同的子数组有多少?
假设以 $nums[i]$ 为最大质数分数的元素,那么什么样的连续子数 $[l,r]$ 组构成符合要求? 则此时一定满足 $[l,i-1]$ 中所有元素的质数分数都小于 $nums[i]$,所有满足 $[i+1,r]$ 的元素的质数分数都要满足小于等于 $nums[i]$, 只要满足上述情况才能构成合法的连续子数组,此时题目似乎就变得简单了,转换为了典型的单调栈。根据乘法原理,可以知道此时可以以 $nums[i]$ 为最大质数分数的连续子数组的数量为 $(i-l + 1)* (r - i + 1)$;
具体单调栈的思路可以参考:2104. 子数组范围和 , 几乎是一样的题目
其余还剩余几个问题需要解决:
如何求元素的质数分数,做法很简单,在这里直接将所有的素数全部筛选了一遍,然后求元素 $x$ 的所有素数因子;
大数的幂,此时可以利用经典的二分法求大数的幂,在这里不再描述;
最后需要处理贪心的问题,按照元素从大到小进行排列,此时我们优先选择尽可能大的元素,C++ 代码写的又臭又长的。
复杂度分析:
时间复杂度:$O(n (\log n + \log U))$,其中 $n$ 表示数组的长度。
空间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
代码 class Solution {public : long long fastpow (long long x, long long n, long long mod) long long res = 1 ; long long cur = x; for (int i = n; i != 0 ; i >>= 1 ) { if (i & 1 ) { res = (res * cur) % mod; } cur = (cur * cur) % mod; } return res; } int maximumScore (vector<int >& nums, int k) int maxVal = *max_element (nums.begin (), nums.end ()); vector<int > arr; vector<int > primer; vector<bool > visit (maxVal + 1 , false ) ; for (int i = 2 ; i <= maxVal; i++) { if (!visit[i]) { primer.emplace_back (i); for (int j = i; j <= maxVal; j += i) { visit[j] = true ; } } } for (int i = 0 ; i < nums.size (); i++) { int x = nums[i], tot = 0 ; for (auto v : primer) { if (x < v) break ; if (x % v == 0 ) { tot++; while (x != 0 && (x % v) == 0 ) { x /= v; } } } arr.emplace_back (tot); } int n = nums.size (); vector<int > left (n) , right (n) ; stack<int > st1; for (int i = 0 ; i < n; i++) { while (!st1.empty () && arr[st1.top ()] < arr[i]) { st1.pop (); } left[i] = st1.empty () ? (i + 1 ) : (i - st1.top ()); st1.emplace (i); } stack<int > st2; for (int i = n - 1 ; i >= 0 ; i--) { while (!st2.empty () && arr[st2.top ()] <= arr[i]) { st2.pop (); } right[i] = st2.empty () ? (n - i) : (st2.top () - i); st2.emplace (i); } vector<pair<int , int >> cnt; for (int i = 0 ; i < n; i++) { cnt.emplace_back (nums[i], right[i] * left[i]); } sort (cnt.begin (), cnt.end (), [&](pair<int , int > &a, pair<int , int > &b) { return a.first > b.first; }); long long ans = 1 ; long long mod = 1e9 + 7 ; for (int i = 0 , j = k; i < n && j > 0 ; i++) { auto [val, freq] = cnt[i]; int tot = min (freq, j); ans = (ans * fastpow (val, tot, mod)) % mod; j -= freq; } return ans; } };
欢迎关注和打赏,感谢支持!