且听疯吟

leetcode biweekly contest 137

2024-08-18

leetcode biweekly contest 137

T4 确实是个不错的题目，值得思考的题目，确实想到了一点思路，但还是关键的一步没有想到，还是三题的节奏。

100384. 长度为 K 的子数组的能量值 II

给你一个长度为 n 的整数数组 nums 和一个正整数 k 。

一个数组的 能量值 定义为：

  • 如果 所有 元素都是依次 连续 且 上升 的，那么能量值为 最大 的元素。
  • 否则为 -1 。

你需要求出 nums 中所有长度为 k 的 子数组 的能量值。

请你返回一个长度为 n - k + 1 的整数数组 results ，其中 results[i] 是子数组 nums[i..(i + k - 1)] 的能量值。

示例 1：

输入：nums = [1,2,3,4,3,2,5], k = 3

输出：[3,4,-1,-1,-1]

解释：

nums 中总共有 5 个长度为 3 的子数组：

  • [1, 2, 3] 中最大元素为 3 。
  • [2, 3, 4] 中最大元素为 4 。
  • [3, 4, 3] 中元素 不是 连续的。
  • [4, 3, 2] 中元素 不是 上升的。
  • [3, 2, 5] 中元素 不是 连续的。

示例 2：

输入：nums = [2,2,2,2,2], k = 4

输出：[-1,-1]

示例 3：

输入：nums = [3,2,3,2,3,2], k = 2

输出：[-1,3,-1,3,-1]

提示：

  • 1 <= n == nums.length <= 105
  • 1 <= nums[i] <= 106
  • 1 <= k <= n

地址

https://leetcode.cn/contest/biweekly-contest-137/problems/find-the-power-of-k-size-subarrays-ii/

题意

模拟

思路

  1. T1 与 T2 的解法完全一致，我们直接计算以 $i$ 为结尾的最长连续能量数组的长度，假设当前的能量长度 $dp[i] > k$ ，此时能量值即为 $nums[i]$，否则为 $-1$。
    • $dp[i] = dp[i - 1] + 1, \quad if nums[i] - nums[i - 1] = 1$;
    • $dp[i] = 1, \quad if nums[i] - nums[i - 1] \neq 1$;
  2. 复杂度分析：
  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(1)$。

代码

class Solution:
    def resultsArray(self, nums: List[int], k: int) -> List[int]:
        ans = []
        tot = 0
        for i, x in enumerate(nums):
            tot = 1 if i == 0 or nums[i] - nums[i - 1] != 1 else tot + 1
            if i >= k - 1:
                ans.append(nums[i] if tot >= k else -1)
        return ans

100401. 放三个车的价值之和最大 II

给你一个 m x n 的二维整数数组 board ，它表示一个国际象棋棋盘，其中 board[i][j] 表示格子 (i, j) 的 价值 。

处于 同一行 或者 同一列 车会互相 攻击 。你需要在棋盘上放三个车，确保它们两两之间都 无法互相攻击 。

请你返回满足上述条件下，三个车所在格子 值 之和 最大 为多少。

示例 1：

输入：board = [[-3,1,1,1],[-3,1,-3,1],[-3,2,1,1]]

输出：4

解释：

img

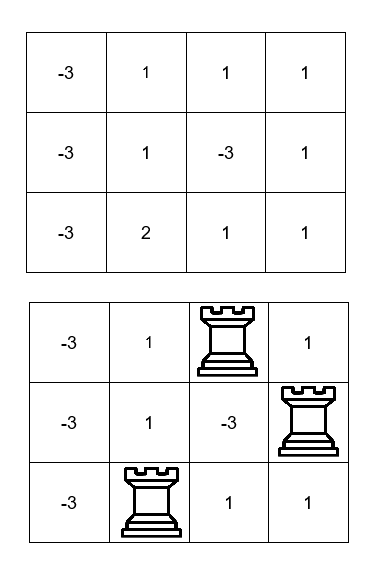
我们可以将车分别放在格子 (0, 2) ，(1, 3) 和 (2, 1) 处，价值之和为 1 + 1 + 2 = 4 。

示例 2：

输入：board = [[1,2,3],[4,5,6],[7,8,9]]

输出：15

解释：

我们可以将车分别放在格子 (0, 0) ，(1, 1) 和 (2, 2) 处，价值之和为 1 + 5 + 9 = 15 。

示例 3：

输入：board = [[1,1,1],[1,1,1],[1,1,1]]

输出：3

解释：

我们可以将车分别放在格子 (0, 2) ，(1, 1) 和 (2, 0) 处，价值之和为 1 + 1 + 1 = 3 。

提示：

  • 3 <= m == board.length <= 500
  • 3 <= n == board[i].length <= 500
  • -109 <= board[i][j] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-137/problems/maximum-value-sum-by-placing-three-rooks-ii/

题意

贪心，动态规划

思路

  1. T3 与 T4的题目完全一致，主要差别在数量级上，先说 t3 比较容易的解法，首先题目要求找到 $3$ 个不再同一列，且不在同一行的三个点之和的最大值，此时我们可以考虑贪心的解法，此时我们找到每一列中的最大的 $3$ 个值，然后枚举 $3$ 个不同的行 $i,j,k$ ，此时我们知道根据排列组合，由于此时我们已经知到 $i,j,k$ 三行中每行的最大的 $3$ 个值，此时我们枚举遍历每行最大值的不同组合，一定可以找到最大的组合出来。此时需要的时间复杂度为 $O(mn + 27m^3 )$, 其中 $m,n$ 表示给定二维矩阵的行与列，贪心的方法比较简单。
  2. t4的的数量级扩大了，此时在按照 t3 的解法就会超时，需要进一步优化。仔细思考一个问题，此时假设最大为不同的 $3$ 行，分别为 $i,j,k, i < j < k$, 我们可以枚举中间最中间的行 $j$ ，此时第 $j$ 行的元素一定出自于第 $j$ 行的最大的 $3$ 个元素之一, 对于 第 $i$ 行的第 $a$ 列的元素，, 此时同一列中按照贪心法则，此时我们应该选择 $board[i’][a]$ 更优。我们首先找到 $0$ 到 $i-1$ 行中所有列中最大得 $3$ 值，同理我们选择第 $k$ 行时也应选择 $j+1$ 到 $n-1$ 中所有列中的最大的 $3$ 个值，思考难度还是比较难得题目，整体还是比较难得题目。
  3. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 表示给定节点的数目。
  • 空间复杂度：$O(n)$；

代码

class Solution:
    def maximumValueSum(self, board: List[List[int]]) -> int:
        m, n = len(board), len(board[0])
        cnt = [[[-inf, -1] for _ in range(3)] for _ in range(m)]
        for i in range(m):
            for j, x in enumerate(board[i]):
                cnt[i].append([x, j])
                cnt[i].sort(key = lambda x : -x[0])
                cnt[i].pop()
        
        res = -inf
        for i in range(m - 2):
            for j in range(i + 1, m - 1):
                for k in range(j + 1, m):
                    for a in range(3):
                        for b in range(3):
                            if cnt[i][a][1] == cnt[j][b][1]:
                                continue
                            for c in range(3):
                                if cnt[k][c][1] == cnt[i][a][1] or cnt[k][c][1] == cnt[j][b][1]:
                                    continue
                                res = max(res, cnt[i][a][0] + cnt[j][b][0] + cnt[k][c][0])
                          
        return res
    
   
class Solution:
    def maximumValueSum(self, board: List[List[int]]) -> int:
        m, n = len(board), len(board[0])
        prefix = [[[-inf, -1] for _ in range(3)] for _ in range(m)]
        suffix = [[[-inf, -1] for _ in range(3)] for _ in range(m)]
        maxThree = [[[-inf, -1] for _ in range(3)] for _ in range(m)]
        
        # prefix[i]: 求出 0~i 行中最大得 3个列
        cnt = [[-inf, -1] for _ in range(n)]
        for i in range(m):
            for j, x in enumerate(board[i]):
                # 求出每一行中得最大得 3 个列
                maxThree[i].append([x, j])
                maxThree[i].sort(key = lambda x : -x[0])
                maxThree[i].pop()
                if x > cnt[j][0]:
                    cnt[j] = [x, j]
            for x, j in cnt:
                prefix[i].append([x, j])
                prefix[i].sort(key = lambda x : -x[0])
                prefix[i].pop()
        
        # suffix[i]: 求出 i~m-1 行中最大得 3个列
        cnt = [[-inf, -1] for _ in range(n)]
        for i in range(m - 1, -1, -1):
            for j, x in enumerate(board[i]):
                if x > cnt[j][0]:
                    cnt[j] = [x, j]
            for x, j in cnt:
                suffix[i].append([x, j])
                suffix[i].sort(key = lambda x : -x[0])
                suffix[i].pop()
            
        res = -inf
        for i in range(1, m - 1):
            for x, a in prefix[i - 1]:
                for y, b in maxThree[i]:
                    if a == b:
                        continue
                    for z, c in suffix[i + 1]:
                        if a == c or b == c:
                            continue
                        res = max(res, x + y + z)                        
                          
        return res

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode weekly contest 410 leetcode weekly contest 411 →

扫描二维码，分享此文章