且听疯吟

leetcode weekly contest 410

2024-08-11

leetcode weekly contest 410

今天周赛比较简单的题目，T3,T4 注意观察规律即可，本质还是动态规划的变形题目，注意观察细节即可，本质上是数学技巧。

100396. 单调数组对的数目 II

给你一个长度为 n 的 正 整数数组 nums 。

如果两个 非负 整数数组 (arr1, arr2) 满足以下条件，我们称它们是 单调 数组对：

  • 两个数组的长度都是 n 。
  • arr1 是单调 非递减 的，换句话说 arr1[0] <= arr1[1] <= ... <= arr1[n - 1] 。
  • arr2 是单调 非递增 的，换句话说 arr2[0] >= arr2[1] >= ... >= arr2[n - 1] 。
  • 对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。

请你返回所有 单调 数组对的数目。

由于答案可能很大，请你将它对 109 + 7 取余 后返回。

示例 1：

输入：nums = [2,3,2]

输出：4

解释：

单调数组对包括：

  1. ([0, 1, 1], [2, 2, 1])
  2. ([0, 1, 2], [2, 2, 0])
  3. ([0, 2, 2], [2, 1, 0])
  4. ([1, 2, 2], [1, 1, 0])

示例 2：

输入：nums = [5,5,5,5]

输出：126

提示：

  • 1 <= n == nums.length <= 2000
  • 1 <= nums[i] <= 1000

地址

https://leetcode.cn/contest/weekly-contest-410/problems/find-the-count-of-monotonic-pairs-ii/

题意

模拟

思路

  1. 直接根据题意模拟即可，按照上下左右四个方向进行模拟即可，返回最终坐标即可；
  2. 复杂度分析：
  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(1)$。

代码

class Solution:
    def finalPositionOfSnake(self, n: int, commands: List[str]) -> int:
        dir = [[0, -1], [0, 1], [-1, 0], [1, 0]]
        x, y = 0, 0
        for command in commands:
            print(command)
            if command == "LEFT":
                x += dir[0][0]
                y += dir[0][1]
            elif command == "RIGHT":
                x += dir[1][0]
                y += dir[1][1]
            elif command == "UP":
                x += dir[2][0]
                y += dir[2][1]
            elif command == "DOWN":
                x += dir[3][0]
                y += dir[3][1]
        
        return x * n + y

100354. 统计好节点的数目

现有一棵 无向 树，树中包含 n 个节点，按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。

如果一个节点的所有子节点为根的 子树 包含的节点数相同，则认为该节点是一个 好节点。

返回给定树中 好节点 的数量。

子树 指的是一个节点以及它所有后代节点构成的一棵树。

示例 1：

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

输出：7

说明：

img

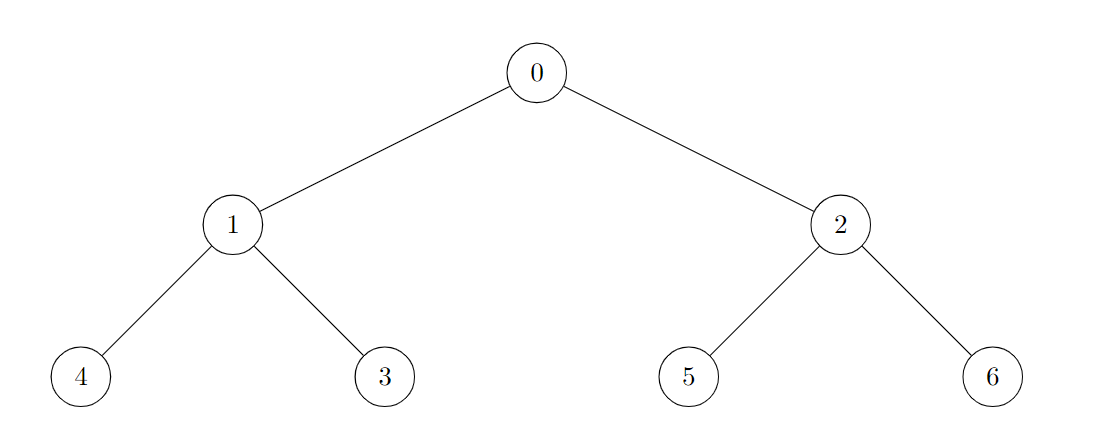
树的所有节点都是好节点。

示例 2：

输入：edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

输出：6

说明：

img

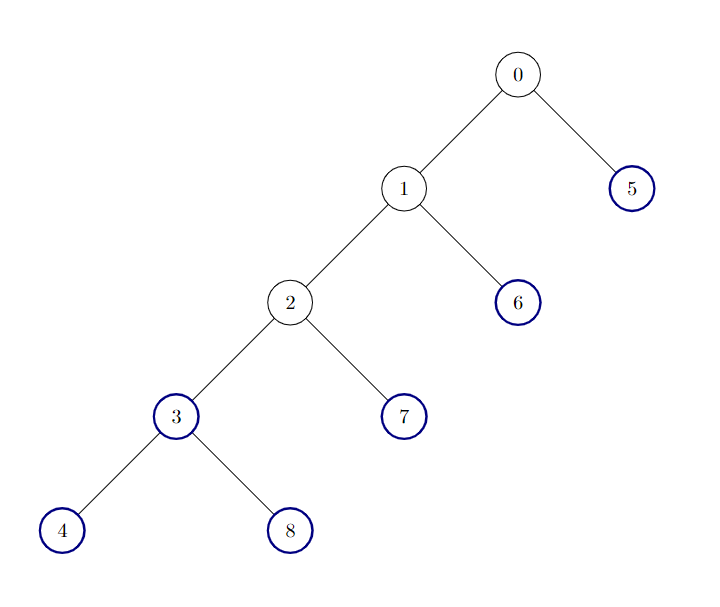
树中有 6 个好节点。上图中已将这些节点着色。

示例 3：

输入：edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

输出：12

解释：

img

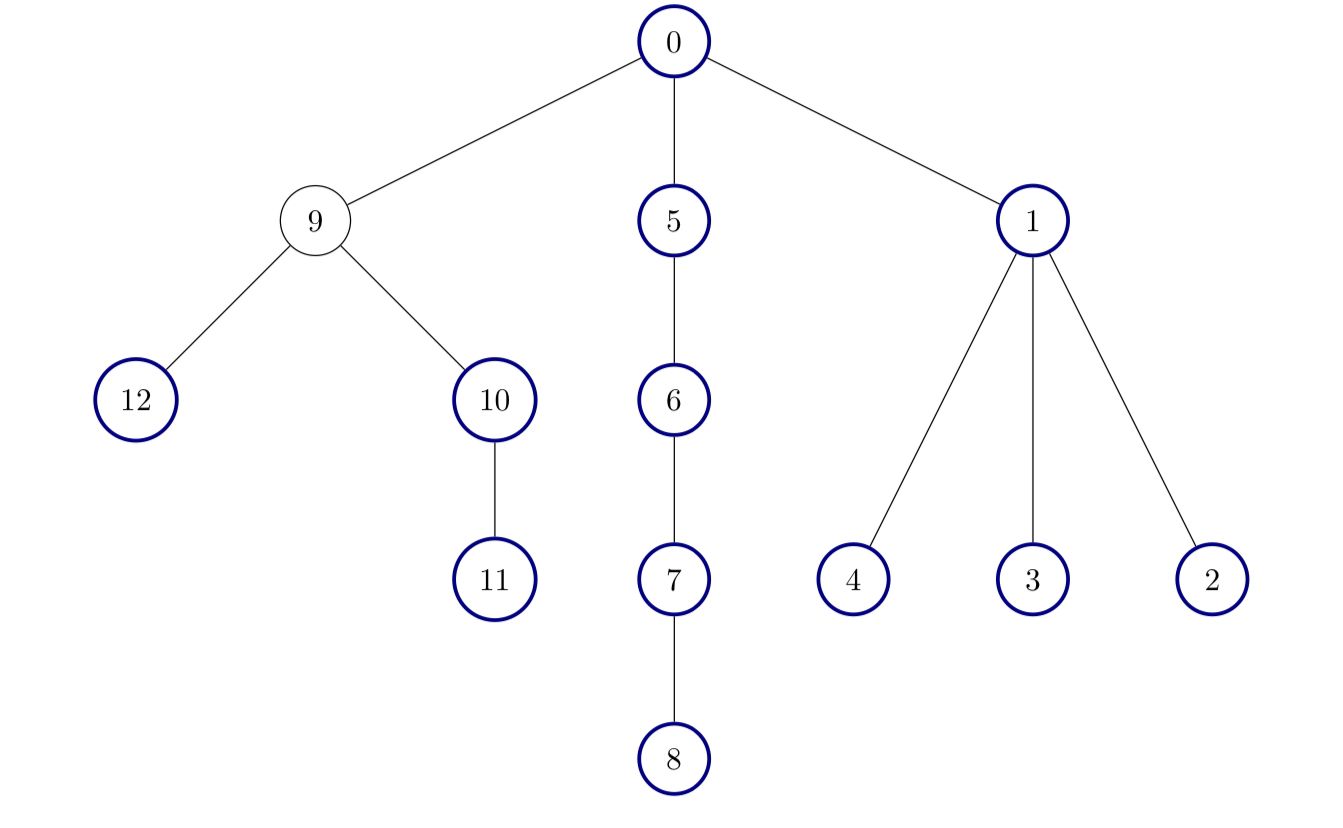
除了节点 9 以外其他所有节点都是好节点。

提示：

  • 2 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • 输入确保 edges 总表示一棵有效的树。

地址

https://leetcode.cn/contest/weekly-contest-410/problems/count-the-number-of-good-nodes/

题意

DFS，树形dp

思路

  1. 在力扣上烂大街的题目了，但是还是按照题意模拟即可，从 $0$ 开始遍历根节点，每次遍历时依次检测当前节点 $v$ 的所有子节点构成的子树种含有的节点数目都相等，如果不相等，则当前节点 $v$ 不是好节点，否则当前节点节点则为好节点，同时返回当前节点 $v$ 的子树中含有的节点数目 $tot$ 即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 表示给定节点的数目。
  • 空间复杂度：$O(n)$；

代码

class Solution:
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        n = len(edges)  + 1
        graph = [[] for _ in range(n)]
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        
        res = 0
        def dfs(v, p):
            nonlocal res
            tot, pre = 1, -1
            valid = True
            for ch in graph[v]:
                if ch == p:
                    continue
                cur = dfs(ch, v)
                tot += cur
                if pre == -1:
                    pre = cur
                elif pre != cur:
                    valid = False
            if valid:
                res += 1
            return tot
        
        dfs(0, -1)
        return res

100395. 单调数组对的数目 I

给你一个长度为 n 的 正 整数数组 nums 。

如果两个 非负 整数数组 (arr1, arr2) 满足以下条件，我们称它们是 单调 数组对：

  • 两个数组的长度都是 n 。
  • arr1 是单调 非递减 的，换句话说 arr1[0] <= arr1[1] <= ... <= arr1[n - 1] 。
  • arr2 是单调 非递增 的，换句话说 arr2[0] >= arr2[1] >= ... >= arr2[n - 1] 。
  • 对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。

请你返回所有 单调 数组对的数目。

由于答案可能很大，请你将它对 109 + 7 取余 后返回。

示例 1：

输入：nums = [2,3,2]

输出：4

解释：

单调数组对包括：

  1. ([0, 1, 1], [2, 2, 1])
  2. ([0, 1, 2], [2, 2, 0])
  3. ([0, 2, 2], [2, 1, 0])
  4. ([1, 2, 2], [1, 1, 0])

示例 2：

输入：nums = [5,5,5,5]

输出：126

提示：

  • 1 <= n == nums.length <= 2000
  • 1 <= nums[i] <= 50

地址

https://leetcode.cn/contest/weekly-contest-410/problems/find-the-count-of-monotonic-pairs-i/

题意

动态规划

思路

  1. 当然我们根据题目给定的数据范围大概就可以知道该题目应该使用动态规划，特别是给定了需要取余，此时更加确定题目需要用到动态规划了。我们设 $dp[i][j]$ 表示 $arr_1$ 中第 $i$ 个元素以 $j$ 为结尾的方案数，此时我们可以知道：

    • 如果 $arr_1$ 中第 $i$ 个元素为 $j$ ，则此时 $arr_2$ 中第 $i$ 个元素则为 $nums[i] - j$;

    • 由于 $arr_1$ 需要满足非递减，$arr_2$ 需要满足非递增，此时 $arr_1[i-1]$ 的取值范围则为 $[0, j]$, 此时 $arr_2[i-1]$ 的值为 $nums[i-1] - arr_1[i-1] \ge nums[i] - arr_1[i]$, 我们将公式变形可以得到 $arr_1[i] - arr_1[i-1] \ge nums[i] - nums[i - 1]$;

    • 假设 $arr_1[i-1]$ 的取值为 $k$，则此时 $k \in[0,j]$, 同时 $nums[i-1] - k \ge nums[i] - j$，即此时 $k \le j - nums[i] + nums[i -1]$；

    • 我们依次从$0$ 开始枚举 $k$，根据上诉结论可以知道递推公式如下：
      $$
      dp[i][j] = \sum_{k=0}^{\min(j, j - nums[i] + nums[i-1])}dp[i-1][k]
      $$

    • 我们根据上诉递推公式依次计算即可。

  2. 复杂度分析：

  • 时间复杂度：$O(n \times U^2)$，其中 $n$ 表示给定数组的长度，$U$ 表示给定数组中元素的最大值;
  • 空间复杂度：$O(n \times U)$, 其中 $n$ 表示给定数组的长度，$U$ 表示给定数组中元素的最大值;

代码

class Solution:
    def countOfPairs(self, nums: List[int]) -> int:
        n, m = len(nums), max(nums)
        mod = 10**9 + 7
        dp = [[0] * (m + 1) for _ in range(n)]
        for i in range(nums[0] + 1):
            dp[0][i] = 1
        for i in range(1, n):
            for j in range(0, nums[i] + 1):
                for k in range(0, j + 1):
                    if nums[i] - j <= nums[i - 1] - k:
                        dp[i][j] = (dp[i][j] + dp[i - 1][k]) % mod
        
        return sum(dp[n - 1]) % mod

100396. 单调数组对的数目 II

给你一个长度为 n 的 正 整数数组 nums 。

如果两个 非负 整数数组 (arr1, arr2) 满足以下条件，我们称它们是 单调 数组对：

  • 两个数组的长度都是 n 。
  • arr1 是单调 非递减 的，换句话说 arr1[0] <= arr1[1] <= ... <= arr1[n - 1] 。
  • arr2 是单调 非递增 的，换句话说 arr2[0] >= arr2[1] >= ... >= arr2[n - 1] 。
  • 对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。

请你返回所有 单调 数组对的数目。

由于答案可能很大，请你将它对 109 + 7 取余 后返回。

示例 1：

输入：nums = [2,3,2]

输出：4

解释：

单调数组对包括：

  1. ([0, 1, 1], [2, 2, 1])
  2. ([0, 1, 2], [2, 2, 0])
  3. ([0, 2, 2], [2, 1, 0])
  4. ([1, 2, 2], [1, 1, 0])

示例 2：

输入：nums = [5,5,5,5]

输出：126

提示：

  • 1 <= n == nums.length <= 2000
  • 1 <= nums[i] <= 1000

地址

https://leetcode.cn/contest/weekly-contest-410/problems/find-the-count-of-monotonic-pairs-ii/

题意

动态规划，前缀和

思路

  1. 根据 T3的思路，我们可以看到实际 $dp[i][j]$ 等于 $dp[i-1]$ 的某个前缀和，根据递推公式可以知道：
    $$
    dp[i][j] = \sum_{k=0}^{\min(j, j - nums[i] + nums[i-1])}dp[i-1][k]
    $$
    我们设 $psum[i][j]$ 表示 $\sum_{k=0}^{j}dp[i][j]$，此时上述等式则变化为前缀和公式如下：
    $$
    dp[i][j] = psum[i-1][min(j, j - nums[i] + nums[i-1])]
    $$
    需要注意的细节是 $x = min(j, j - nums[i] + nums[i-1])$ 可能出现小于 $0$ 的情形，我们需要剔除该异常情况即可。

  2. 复杂度分析：

  • 时间复杂度：$O(n \times U)$，其中 $n$ 表示给定数组的长度，$U$ 表示给定数组中元素的最大值;
  • 空间复杂度：$O(n \times U)$, 其中 $n$ 表示给定数组的长度，$U$ 表示给定数组中元素的最大值;

代码

class Solution:
    def countOfPairs(self, nums: List[int]) -> int:
        n, m = len(nums), max(nums)
        mod = 10**9 + 7
        dp = [[0] * (m + 1) for _ in range(n)]
        psum = [[0] * (m + 1) for _ in range(n)]
        for i in range(nums[0] + 1):
            dp[0][i] = 1
            psum[0][i] = i + 1
        for i in range(1, n):
            for j in range(0, nums[i] + 1):
                x = min(nums[i - 1], j, j - nums[i] + nums[i - 1])
                if x >= 0:
                    dp[i][j] = (dp[i][j] + psum[i - 1][x]) % mod
            for j in range(0, nums[i] + 1):
                psum[i][j] = dp[i][j]
                if j > 0:
                    psum[i][j] = (psum[i][j] + psum[i][j - 1]) % mod
        return psum[n - 1][nums[-1]]

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode weekly contest 408 leetcode biweekly contest 137 →

扫描二维码，分享此文章