leetcode weekly contest 408

今天的t3,t4 果然有难度，但是 t4 题目存在问题，刚开始就想到了用集合的方法，但是无法检测圆心在矩形外的情况。

100377. 判断是否可以赢得数字游戏

给你一个 正整数 数组 nums。

小红和小明正在玩游戏。在游戏中，小红可以从 nums 中选择所有个位数 或 所有两位数，剩余的数字归小明所有。如果小红所选数字之和 严格大于 小明的数字之和，则小红获胜。

如果小红能赢得这场游戏，返回 true；否则，返回 false。

示例 1：

输入：nums = [1,2,3,4,10]

输出：false

解释：

小红不管选个位数还是两位数都无法赢得比赛。

示例 2：

输入：nums = [1,2,3,4,5,14]

输出：true

解释：

小红选择个位数可以赢得比赛，所选数字之和为 15。

示例 3：

输入：nums = [5,5,5,25]

输出：true

解释：

小红选择两位数可以赢得比赛，所选数字之和为 25。

提示：

• 1 <= nums.length <= 100
• 1 <= nums[i] <= 99

地址

https://leetcode.cn/contest/weekly-contest-408/problems/find-if-digit-game-can-be-won/

题意

模拟

思路

1. 直接检测数组中所有小于 $10$ 的元素之和与大于 $10$ 的元素之和不相等即可，否则直接取最大的值即可赢得游戏；
2. 复杂度分析：

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def canAliceWin(self, nums: List[int]) -> bool:
        return sum(x for x in nums if x < 10) * 2 != sum(nums)

100371. 统计不是特殊数字的数字数量

给你两个 正整数 l 和 r。对于任何数字 x，x 的所有正因数（除了 x 本身）被称为 x 的 真因数。

如果一个数字恰好仅有两个 真因数，则称该数字为 特殊数字。例如：

• 数字 4 是 特殊数字，因为它的真因数为 1 和 2。
• 数字 6 不是 特殊数字，因为它的真因数为 1、2 和 3。

返回区间 [l, r] 内 不是 特殊数字 的数字数量。

示例 1：

输入： l = 5, r = 7

输出： 3

解释：

区间 [5, 7] 内不存在特殊数字。

示例 2：

输入： l = 4, r = 16

输出： 11

解释：

区间 [4, 16] 内的特殊数字为 4 和 9。

提示：

• 1 <= l <= r <= 109

地址

https://leetcode.cn/contest/weekly-contest-408/problems/find-the-count-of-numbers-which-are-not-special/

题意

模拟

思路

1. 仔细思考可以直到此时 $x$ 为特殊数字，则必须满足以下几个条件：
   • $x = y^2$，且此时 $x$ 只有 $1, y, x$ 这三个因子；
   • $y$ 此时必须是素数，否则一定多余 $3$ 个因子；
   • 此时我们尝试检测存在多少个素数 $y$，满足 $y^2 \in [l,r]$ 即可；
2. 复杂度分析：

• 时间复杂度：$O(\sqrt{n} \times \sqrt{\sqrt{n}})$，其中 $n$ 表示给定的数字。
• 空间复杂度：$O(1)$；

代码

class Solution:
    def nonSpecialCount(self, l: int, r: int) -> int:
        def is_primer(x) -> bool:
            for i in range(2, int(math.sqrt(x)) + 1):
                if x % i == 0:
                    return False
            return True
        
        cnt = 0
        for i in range(max(2, int(math.sqrt(l))), int(math.sqrt(r)) + 1):
            if i**2 >= l and i**2 <= r and is_primer(i):
                cnt += 1
        return r - l + 1 - cnt

100348. 统计 1 显著的字符串的数量

给你一个二进制字符串 s。

请你统计并返回其中 1 显著 的 子字符串 的数量。

如果字符串中 1 的数量 大于或等于 0 的数量的 平方，则认为该字符串是一个 1 显著 的字符串 。

示例 1：

输入：s = “00011”

输出：5

解释：

1 显著的子字符串如下表所示。

示例 2：

输入：s = “101101”

输出：16

解释：

1 不显著的子字符串如下表所示。

总共有 21 个子字符串，其中 5 个是 1 不显著字符串，因此有 16 个 1 显著子字符串。

提示：

• 1 <= s.length <= 4 * 104
• s 仅包含字符 '0' 和 '1'。

地址

https://leetcode.cn/contest/weekly-contest-408/problems/count-the-number-of-substrings-with-dominant-ones/

题意

直接枚举

思路

1. 假设当前字符串的长度为 $n$ , 由于需要满足 $1$ 的数目大于等于 $0$ 的数目的平方，此时根据题意可以直到，所有显著 字符串中 $0$ 的数目一定不超过 $\sqrt{n}$ 个，此时固定子字符串的左端点或者右端点，然后枚举 $0$ 的数目直到 $0$ 的数目大于 $\sqrt{n}$ 个则中止即可，但是枚举的时候需要一些技巧，还是非常好的思维题目，希望这样的题目多来几个, 假设当前子字符串的右端点为 $i$，则可以知道：
   • 此时我们从右向左枚举 $0$ 的数目，假设我们当前枚举到第 $k$ 个 $0$，且此时第 $k$ 个 $0$ 的索引为 $pos[k]$，则此时可以知道字符串 $s[pos[k]\cdots i]$ 中含有 $0$ 的数目为 $c_0 = k$ 个，$1$ 的数目为则为 $c_1 = i - pos[k] + 1 - k$，
     • 此时如果满足 $c_0^2 \le c_1$, 则此时可以知道任意增加 $1$ 的字符串一定也是 显著 的，由于下一个 $0$ 的位置为 $pos[k-1]$ , 此时 $s[(pos[k-1] + 1)\cdots i],s[(pos[k-1] + 2)\cdots i], \cdots, s[pos[k]\cdots i]$ 均为 显著 字符串，一共可以增加 $pos[k] - pos[k-1]$ 个 显著 字符串；
     • 此时如果满足 $c_0^2 > c_1$, 则此时可以知道至少还需要增加 $d = c_1-c_2^2$ 个 $1$ 才能使得字符串构成 显著 ，由于下一个 $0$ 的位置为 $pos[k-1]$ , 此时如果 $pos[k] - pos[k-1] < d$，则表示两个 $0$ 之间的 $1$ 即使全部加进来也无法构成 显著 字符串，此时如果 $pos[k] - pos[k-1] \ge d$，则表示两个 $0$ 之间的 $1$ 即使全部加进来一定可以 显著 字符串，但是最多只能构成 $pos[k] - pos[k - 1] - d$ 个显著字符串；
   • 题目本身的思路确实不太好想，利用题目的提示来枚举，确实非常好的思维题目，基本上不需要数据结构即可。
2. 复杂度分析：

• 时间复杂度：$O(\sqrt{n})$，其中 $n$ 表示给定字符串的长度;
• 空间复杂度：$O(\sqrt{n})$;

代码

class Solution:
    def numberOfSubstrings(self, s: str) -> int:
        pos = [-1]
        res, tot = 0, 0
        for i, c in enumerate(s):
            if c == '0':
                pos.append(i)
            else:
                tot += 1
                res += i - pos[-1]
            for j in range(len(pos) - 1, 0, -1):
                cnt0 = len(pos) - j
                cnt1 = i - pos[j] + 1 - cnt0
                if cnt0**2 > tot:
                    break
                d = cnt0 * cnt0 - cnt1
                if d <= 0:
                    res += pos[j] - pos[j - 1]
                else:
                    res += max(0, pos[j] - pos[j - 1] - d)
        
        return res

100347. 判断矩形的两个角落是否可达

给你两个正整数 X 和 Y 和一个二维整数数组 circles ，其中 circles[i] = [xi, yi, ri] 表示一个圆心在 (xi, yi) 半径为 ri 的圆。

坐标平面内有一个左下角在原点，右上角在 (X, Y) 的矩形。你需要判断是否存在一条从左下角到右上角的路径满足：路径 完全 在矩形内部，不会 触碰或者经过 任何 圆的内部和边界，同时 只 在起点和终点接触到矩形。

如果存在这样的路径，请你返回 true ，否则返回 false 。

示例 1：

输入：X = 3, Y = 4, circles = [[2,1,1]]

输出：true

解释：

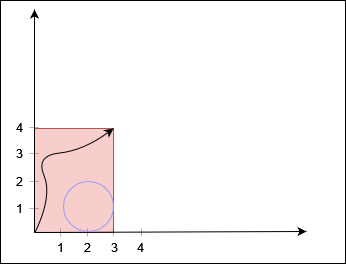
黑色曲线表示一条从 (0, 0) 到 (3, 4) 的路径。

示例 2：

输入：X = 3, Y = 3, circles = [[1,1,2]]

输出：false

解释：

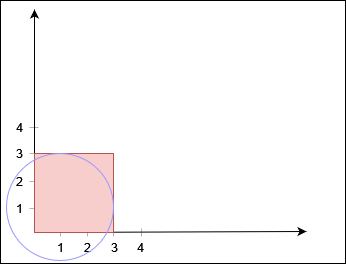
不存在从 (0, 0) 到 (3, 3) 的路径。

示例 3：

输入：X = 3, Y = 3, circles = [[2,1,1],[1,2,1]]

输出：false

解释：

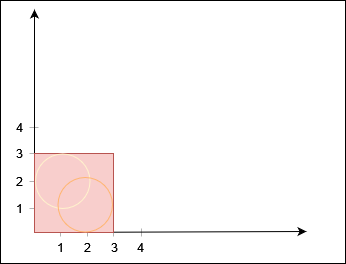
不存在从 (0, 0) 到 (3, 3) 的路径。

提示：

• 3 <= X, Y <= 109
• 1 <= circles.length <= 1000
• circles[i].length == 3
• 1 <= xi, yi, ri <= 109

地址

https://leetcode.cn/problems/check-if-the-rectangle-corner-is-reachable/

题意

并查集，计算几何

思路

1.
2.
3. 复杂度分析：

• 时间复杂度：$O((m + n) \log (m + n)$，其中 $m,n$ 表示给的数；
• 空间复杂度：$O(m + n)$，其中 $m,n$ 表示给的数；

代码

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu

• 关注我的微信公众号: 哪些奋斗者