leetcode biweekly contest 135

100375. 求出硬币游戏的赢家

给你两个正整数 x 和 y ，分别表示价值为 75 和 10 的硬币的数目。

Alice 和 Bob 正在玩一个游戏。每一轮中，Alice 先进行操作，Bob 后操作。每次操作中，玩家需要拿出价值总和为 115 的硬币。如果一名玩家无法执行此操作，那么这名玩家输掉游戏。

两名玩家都采取最优策略，请你返回游戏的赢家。

示例 1：

输入：x = 2, y = 7

输出：“Alice”

解释：

游戏一次操作后结束：

Alice 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。

示例 2：

输入：x = 4, y = 11

输出：“Bob”

解释：

游戏 2 次操作后结束：

Alice 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。
Bob 拿走 1 枚价值为 75 的硬币和 4 枚价值为 10 的硬币。

提示：

1 <= x, y <= 100

地址

https://leetcode.cn/contest/biweekly-contest-135/problems/find-the-winning-player-in-coin-game/

题意

模拟

思路

统计可以拿走的次数即可，如果次数为奇数则是 $Alice$ 赢，否则则是 $bob$ 赢掉比赛；
复杂度分析：

时间复杂度：$O(1)$。
空间复杂度：$O(1)$。

代码

class Solution:
    def losingPlayer(self, x: int, y: int) -> str:
        a = min(x, y //4)
        if a & 1 == 1:
            return "Alice"
        else:
            return "Bob"

100330. 操作后字符串的最短长度

给你一个字符串 s 。

你需要对 s 执行以下操作任意次：

选择一个下标 i ，满足 s[i] 左边和右边都至少有一个字符与它相同。
删除 s[i] 左边离它最近且相同的字符。
删除 s[i] 右边离它最近且相同的字符。

请你返回执行完所有操作后， s 的最短长度。

示例 1：

输入：s = “abaacbcbb”

输出：5

解释：
我们执行以下操作：

选择下标 2 ，然后删除下标 0 和 3 处的字符，得到 s = "bacbcbb" 。
选择下标 3 ，然后删除下标 0 和 5 处的字符，得到 s = "acbcb" 。

示例 2：

输入：s = “aa”

输出：2

解释：
无法对字符串进行任何操作，所以返回初始字符串的长度。

提示：

1 <= s.length <= 2 * 105
s 只包含小写英文字母。

地址

https://leetcode.cn/contest/biweekly-contest-135/problems/minimum-length-of-string-after-operations/

题意

模拟

思路

本质即为统计字符串中字符串的数目，假设给定字符 $c$ 在字符串中出现的此时为 $x$，此时则有以下推论：
- 如果 $x$ 为奇数，且满足 $x > 1$ , 此时我们每次选择最中间的字符串，然后依次减少两边的字符，最终字符剩余为 $1$ 个；
- 如果 $x$ 为偶数，此时每次只能选择减少两个字符串，直到最终的字符串剩余 $2$ 个后则再也无法减少；
- 如果 $x$ 等于 $1,2$ ，则此时无法继续减少，直接返回即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示给定字符串的长度。
空间复杂度：$O(|\Sigma|)$，其中 $O(|\Sigma|)$ 表示给定的数组的长度

代码

class Solution:
    def minimumLength(self, s: str) -> int:
        cnt = Counter(s)
        res = 0
        for _, x in cnt.items():
            if x <= 2:
                res += x
            else:
                if x % 2 == 1:
                    res += 1
                else:
                    res += 2
        return res

3224. 使差值相等的最少数组改动次数

给你一个长度为 n 的整数数组 nums ，n 是偶数，同时给你一个整数 k 。

你可以对数组进行一些操作。每次操作中，你可以将数组中任一元素替换为 0 到 k 之间的任一整数。

执行完所有操作以后，你需要确保最后得到的数组满足以下条件：

存在一个整数 X ，满足对于所有的 (0 <= i < n) 都有 abs(a[i] - a[n - i - 1]) = X 。

请你返回满足以上条件最少修改次数。

示例 1：

输入：nums = [1,0,1,2,4,3], k = 4

输出：2

解释：
我们可以执行以下操作：

将 nums[1] 变为 2 ，结果数组为 nums = [1,***2***,1,2,4,3] 。
将 nums[3] 变为 3 ，结果数组为 nums = [1,2,1,***3***,4,3] 。

整数 X 为 2 。

示例 2：

输入：nums = [0,1,2,3,3,6,5,4], k = 6

输出：2

解释：
我们可以执行以下操作：

将 nums[3] 变为 0 ，结果数组为 nums = [0,1,2,***0***,3,6,5,4] 。
将 nums[4] 变为 4 ，结果数组为 nums = [0,1,2,0,***4***,6,5,4] 。

整数 X 为 4 。

提示：

2 <= n == nums.length <= 105
n 是偶数。
0 <= nums[i] <= k <= 105

地址

https://leetcode.cn/contest/biweekly-contest-135/problems/minimum-array-changes-to-make-differences-equal/

题意

枚举，差分数组

思路

非常不错的思维题目，还是挺好的题目，关键在于分析什么时候需要修改 $1$ 次，什么时候需要修改 $2$ 次，这个是这个题目的关键，对于给定的两个数 $p, q$ ，且满足 $p < q$，假设当前给定 $X$，需要操作使得 $|p- q| = X$，具体需要分析如下：
- 如果满足 $q - p = X$, 此时需要修改 $0$ 次；
- 如果满足 $p-q > X$，此时只需要修改 $1$ 次；
- 如果满足 $q \ge X$ 或者 $p \le k - X$ 时，此时只需要修改 $1$ 次；
- 如果满足 $q < X$ 且满足 $p > k - X$ 时，此时一定需要修改 $2$ 次才可以，此时满足 $q < X, k - p < X$，即此时需要满足 $\max(q, k - p) < X$ 时，需要修改 $2$ 次，这是条件判断是本题的关键，即如何判断满足什么条件下需要进行 $2$ 次修改。
根据上诉分析，此时我们枚举 $X$，同时计算满足 $\max(q, k - p) < X$ 的数对的数目，此时即可快速计算出来需要修改的次数。
差分数组的思路也非常有意思，我们用差分数组的思想，对于 $\sum_{0}^{i}cnt[j]$ 表示当前绝对值为 $i$ 时整个数组需要修改的次数，假设当前两个元素的差值为 $x = p -q$，此时我们可以分析如下：
- 此时当 $X \in [0,x-1]$ 时，数对 $(p,q)$ 只需要修改 $1$ 次；
- 此时当 $X = x$ 时，数对 $(p,q)$ 只需要修改 $0$ 次；
- 此时当 $X \in [x + 1, \max(q, k - p)]$ 时，数对 $(p,q)$ 只需要修改 $1$ 次；
- 此时当 $X \in (\max(q, k - p), k]$ 时，数对 $(p,q)$ 只需要修改 $2$ 次；
- 因此我们可以使用差分的思想即可，但是整体思考过程还是挺难的，还是方法一比较直接且比较容易思考。
复杂度分析：

时间复杂度：$O(n + k)$，其中 $n$ 表示给定数组的长度， $k$ 表示给定的数字；
空间复杂度：$O(k)$，其中 $k$ 表示给定的数字；

代码

class Solution:
    def minChanges(self, nums: List[int], k: int) -> int:
        n = len(nums)
        cnt1 = [0] * (k + 1)
        cnt2 = [0] * (k + 1)
        for i in range(0, n // 2):
            x, y = nums[i], nums[n - 1 - i]
            cnt1[abs(x - y)] += 1
            cnt2[max(max(x, y), k - min(x, y))] += 1
        
        res, pre = n, 0
        for i in range(k + 1):
            res = min(res, n // 2 - cnt1[i] + pre)
            pre += cnt2[i]
        return res

class Solution:
    def minChanges(self, nums: List[int], k: int) -> int:
        n = len(nums)
        d = [0] * (k + 2)
        for i in range(n // 2):
            p, q = nums[i], nums[n - 1 - i]
            if p > q:
                p, q = q, p
            x = q - p
            mx = max(q, k - p)
            d[0] += 1
            d[x] -= 1
            d[x + 1] += 1
            d[mx + 1] += 1
        return min(accumulate(d))

3225. 网格图操作后的最大分数

给你一个大小为 n x n 的二维矩阵 grid ，一开始所有格子都是白色的。一次操作中，你可以选择任意下标为 (i, j) 的格子，并将第 j 列中从最上面到第 i 行所有格子改成黑色。

如果格子 (i, j) 为白色，且左边或者右边的格子至少一个格子为黑色，那么我们将 grid[i][j] 加到最后网格图的总分中去。

请你返回执行任意次操作以后，最终网格图的最大总分数。

示例 1：

输入：grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]

输出：11

解释：

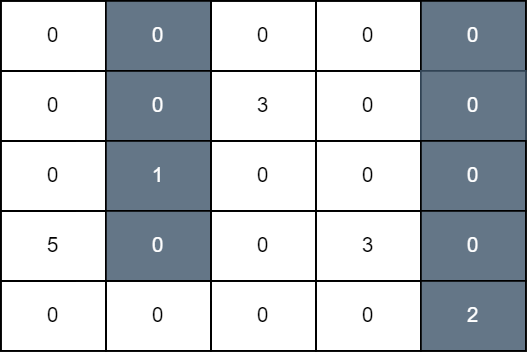
第一次操作中，我们将第 1 列中，最上面的格子到第 3 行的格子染成黑色。第二次操作中，我们将第 4 列中，最上面的格子到最后一行的格子染成黑色。最后网格图总分为 grid[3][0] + grid[1][2] + grid[3][3] 等于 11 。

示例 2：

输入：grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]

输出：94

解释：

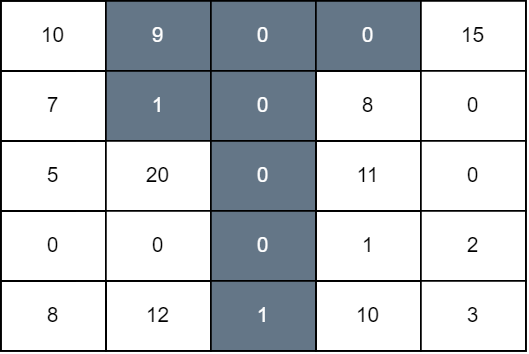
我们对第 1 ，2 ，3 列分别从上往下染黑色到第 1 ，4， 0 行。最后网格图总分为 grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] 等于 94 。

提示：

1 <= n == grid.length <= 100
n == grid[i].length
0 <= grid[i][j] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-135/problems/maximum-score-from-grid-operations/

题意

贪心

思路

1.
2. 复杂度分析：

时间复杂度：$O((m + n) \log (m + n)$，其中 $m,n$ 表示给的数；
空间复杂度：$O(m + n)$，其中 $m,n$ 表示给的数；

代码

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 哪些奋斗者

Tags: 题解力扣周赛赛

← leetcode weekly contest 406 leetcode weekly contest 407 →

扫描二维码，分享此文章