leetcode weekly contest 407 3226. 使两个整数相等的位更改次数 给你两个正整数 n 和 k。
你可以选择 n 的 二进制表示 中任意一个值为 1 的位,并将其改为 0。
返回使得 n 等于 k 所需要的更改次数。如果无法实现,返回 -1。
示例 1:
输入: n = 13, k = 4
输出: 2
解释: n 和 k 的二进制表示分别为 n = (1101)2 和 k = (0100)2,
我们可以改变 n 的第一位和第四位。结果整数为 n = (**0**10**0**)2 = k。
示例 2:
输入: n = 21, k = 21
输出: 0
解释: n 和 k 已经相等,因此不需要更改。
示例 3:
输入: n = 14, k = 13
输出: -1
解释: n 等于 k。
提示:
地址 https://leetcode.cn/contest/weekly-contest-407/problems/number-of-bit-changes-to-make-two-integers-equal/
题意 直接模拟
思路 1.
时间复杂度:$O(n)$。
空间复杂度:$O(1)$。
代码 class Solution : def getEncryptedString (self, s: str , k: int ) -> str : return s[k % len (s):] + s[0 : k % len (s)]
3211. 生成不含相邻零的二进制字符串 给你一个正整数 n。
如果一个二进制字符串 x 的所有长度为 2 的子字符串中包含 至少 一个 "1",则称 x 是一个 有效 字符串。
返回所有长度为 n 的 有效 字符串,可以以任意顺序排列。
示例 1:
输入: n = 3
输出: [“010”,”011”,”101”,”110”,”111”]
解释:
长度为 3 的有效字符串有:"010"、"011"、"101"、"110" 和 "111"。
示例 2:
输入: n = 1
输出: [“0”,”1”]
解释:
长度为 1 的有效字符串有:"0" 和 "1"。
提示:
地址 https://leetcode.cn/contest/weekly-contest-405/problems/generate-binary-strings-without-adjacent-zeros/
题意 模拟,枚举
思路
嘴贱但
复杂度分析:
时间复杂度:$O(n \log n )$,其中 $n$ 表示给定数组的长度。
空间复杂度:$O(\log n)$,其中 $n$ 表示给定数组的长度。
代码 class Solution : def validStrings (self, n: int ) -> List [str ]: ans = [] mask = (1 << n) - 1 for i in range (1 << n): x = mask ^ i if (x >> 1 ) & x == 0 : ans.append(f"{i:0 {n} b}" ) return ans
3212. 统计 X 和 Y 频数相等的子矩阵数量 给你一个二维字符矩阵 grid,其中 grid[i][j] 可能是 'X'、'Y' 或 '.',返回满足以下条件的子矩阵数量:
包含 grid[0][0]
'X' 和 'Y' 的频数相等。至少包含一个 'X'。
示例 1:
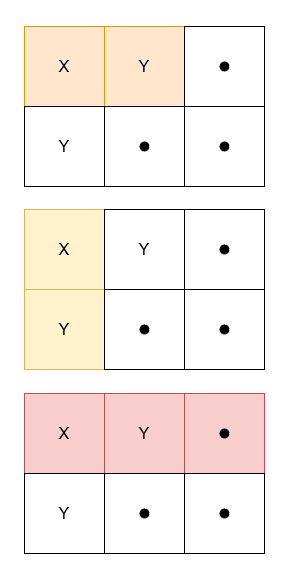
输入: grid = [[“X”,”Y”,”.”],[“Y”,”.”,”.”]]
输出: 3
解释:
示例 2:
输入: grid = [[“X”,”X”],[“X”,”Y”]]
输出: 0
解释:
不存在满足 'X' 和 'Y' 频数相等的子矩阵。
示例 3:
输入: grid = [[“.”,”.”],[“.”,”.”]]
输出: 0
解释:
不存在满足至少包含一个 'X' 的子矩阵。
提示:
1 <= grid.length, grid[i].length <= 1000grid[i][j] 可能是 'X'、'Y' 或 '.'.
地址 https://leetcode.cn/contest/weekly-contest-405/problems/count-submatrices-with-equal-frequency-of-x-and-y/
题意
动态规划
思路
我们利用动态规划可以统计所有以 $(0,0),(i,j)$ 组成的矩形中的 $x$ 与 $y$ 的数量,动态规划方程很容易写:
我们求出所有位置中 $x,y$ 的统计数目,并按照题目要求检测是否满足数量是否相等即可。
复杂度分析:
时间复杂度:$O(mn)$,其中 $mn$ 表示给定矩阵的行数与列数。
空间复杂度:$O(mn)$,其中 $mn$ 表示给定矩阵的行数与列数。
代码 class Solution : def numberOfSubmatrices (self, grid: List [List [str ]] ) -> int : m, n = len (grid), len (grid[0 ]) res = 0 dp1 = [[0 ] * (n + 1 ) for _ in range (m + 1 )] dp2 = [[0 ] * (n + 1 ) for _ in range (m + 1 )] for i in range (m): for j in range (n): dp1[i + 1 ][j + 1 ] = dp1[i][j + 1 ] + dp1[i + 1 ][j] - dp1[i][j] dp2[i + 1 ][j + 1 ] = dp2[i][j + 1 ] + dp2[i + 1 ][j] - dp2[i][j] if grid[i][j] == 'X' : dp1[i + 1 ][j + 1 ] += 1 if grid[i][j] == 'Y' : dp2[i + 1 ][j + 1 ] += 1 if dp1[i + 1 ][j + 1 ] > 0 and dp1[i + 1 ][j + 1 ] == dp2[i + 1 ][j + 1 ]: res += 1 return res
3213. 最小代价构造字符串 给你一个字符串 target、一个字符串数组 words 以及一个整数数组 costs,这两个数组长度相同。
设想一个空字符串 s。
你可以执行以下操作任意次数(包括零 次):
选择一个在范围 [0, words.length - 1] 的索引 i。
将 words[i] 追加到 s。
该操作的成本是 costs[i]。
返回使 s 等于 target 的 最小 成本。如果不可能,返回 -1。
示例 1:
输入: target = “abcdef”, words = [“abdef”,”abc”,”d”,”def”,”ef”], costs = [100,1,1,10,5]
输出: 7
解释:
选择索引 1 并以成本 1 将 "abc" 追加到 s,得到 s = "abc"。
选择索引 2 并以成本 1 将 "d" 追加到 s,得到 s = "abcd"。
选择索引 4 并以成本 5 将 "ef" 追加到 s,得到 s = "abcdef"。
示例 2:
输入: target = “aaaa”, words = [“z”,”zz”,”zzz”], costs = [1,10,100]
输出: -1
解释:
无法使 s 等于 target,因此返回 -1。
提示:
1 <= target.length <= 5 * 1041 <= words.length == costs.length <= 5 * 1041 <= words[i].length <= target.length所有 words[i].length 的总和小于或等于 5 * 104
target 和 words[i] 仅由小写英文字母组成。1 <= costs[i] <= 104
地址 https://leetcode.cn/contest/weekly-contest-405/problems/construct-string-with-minimum-cost/
题意
AC自动机,字符串哈希
思路
题目还是比较经典,并且难度较高的题目,仔细看了 AC 的代码中有一半估计应该过不了的,力扣的测试用力不够强大。还是正统的用经典算法,当然字符串哈希的算法比较容易理解。当然题目看起来很直接的动态规划,设 $dp[i]$ 表示 $target$ 从 $0$ 到 $i-1$ 最小构造开销,此时我们可以知道假设子字符串 $taget[j\cdots i-1]$ 可以被 $words$ 种某个字符串替换,此时可以得到递推公式如下:
首先我们需要计算一下给定的字符串数组 $words$ 中不同字符串长度的数目,设所有字符串的长度之和为 $m$,此时最多的数目种类即为 $1+2+3+…+ q = m$,此时 $\dfrac{q\times(q + 1)}{2} = m$, 此时可以得到 $q \le \sqrt{2m}$, 因此不同的长度种类最多有 $\sqrt{2m}$ 种。
利用 AC 自动机匹配,也是一个经典的模板题目,但是 AC 自动机一般写起来比较麻烦,确实现场不看模板的话真心写不出来,每次自己写这个 ac自动机以后都会忘掉,遇到这题还是老老实实写字符串哈希。
复杂度分析:
时间复杂度:$O(n \log n)$,其中 $n$ 表示给定字符串的长度。
空间复杂度:$O(n)$,其中 $n$ 表示给定字符串的长度。
代码 class Solution {public: static constexpr long long mod = 1e9 + 7 ; static constexpr long long base = 31 ; int minimumCost(string target, vector<string>& words, vector<int >& costs) { int n = target.size(); vector<long long> hbase(n + 1 , 1 ); vector<long long> pre(n + 1 ); for (int i = 0 ; i < n; i++) { hbase[i + 1 ] = hbase[i] * base % mod; pre[i + 1 ] = (pre[i] * base + target[i] - 'a' ) % mod; } /* 计算当前长度的哈希值 */ auto get = [&](int pos, int len ) -> long long { return (pre[pos] - (pre[pos - len ] * hbase[len ] % mod) + mod) % mod; }; map <int , unordered_map<long long, int >> cnt; for (int i = 0 ; i < words.size(); i++) { long long cur = 0 ; int len = words[i].size(); for (char c : words[i]) { cur = (cur * base + c - 'a' ) % mod; } if (cnt[len ].find(cur) != cnt[len ].end()) { cnt[len ][cur] = min (cnt[len ][cur], costs[i]); } else { cnt[len ][cur] = costs[i]; } } vector<int > dp(n + 1 , INT_MAX); dp[0 ] = 0 ; for (int i = 1 ; i <= n; i++) { for (auto &[len , mp] : cnt) { if (len > i) break ; if (dp[i - len ] == INT_MAX) continue ; long long key = get(i, len ); if (mp.count(key)) { dp[i] = min (dp[i], dp[i - len ] + mp[key]); } } } return dp[n] == INT_MAX ? -1 : dp[n]; } }; struct Node { Node* son[26 ]{}; Node* fail; // 当 cur.son[i] 不能匹配 target 中的某个字符时,cur.fail.son[i] 即为下一个待匹配节点(等于 root 则表示没有匹配) Node* last; // 后缀链接(suffix link),用来快速跳到一定是某个 words[k] 的最后一个字母的节点(等于 root 则表示没有) int len = 0 ; int cost = INT_MAX; }; struct AhoCorasick { Node* root = new Node(); void put(string& s, int cost) { auto cur = root; for (char b : s) { b -= 'a' ; if (cur->son[b] == nullptr) { cur->son[b] = new Node(); } cur = cur->son[b]; } cur->len = s.length(); cur->cost = min (cur->cost, cost); } void build_fail() { root->fail = root->last = root; queue<Node*> q; for (auto& son : root->son) { if (son == nullptr) { son = root; } else { son->fail = son->last = root; // 第一层的失配指针,都指向根节点 ∅ q.push(son); } } // BFS while (!q.empty()) { auto cur = q.front(); q.pop(); for (int i = 0 ; i < 26 ; i++) { auto& son = cur->son[i]; if (son == nullptr) { // 虚拟子节点 cur.son[i],和 cur.fail.son[i] 是同一个 // 方便失配时直接跳到下一个可能匹配的位置(但不一定是某个 words[k] 的最后一个字母) son = cur->fail->son[i]; continue ; } son->fail = cur->fail->son[i]; // 计算失配位置 // 沿着 last 往上走,可以直接跳到一定是某个 words[k] 的最后一个字母的节点(如果跳到 root 表示没有匹配) son->last = son->fail->len ? son->fail : son->fail->last; q.push(son); } } } }; class Solution {public: int minimumCost(string target, vector<string>& words, vector<int >& costs) { AhoCorasick ac; for (int i = 0 ; i < words.size(); i++) { ac.put(words[i], costs[i]); } ac.build_fail(); int n = target.size(); vector<int > f(n + 1 , INT_MAX / 2 ); f[0 ] = 0 ; auto cur = ac.root; for (int i = 1 ; i <= n; i++) { cur = cur->son[target[i - 1 ] - 'a' ]; // 如果没有匹配相当于移动到 fail 的 son[target[i-1 ]-'a' ] if (cur->len ) { // 匹配到了一个尽可能长的 words[k] f[i] = min (f[i], f[i - cur->len ] + cur->cost); } // 还可能匹配其余更短的 words[k],要在 last 链上找 for (auto match = cur->last; match != ac.root; match = match ->last) { f[i] = min (f[i], f[i - match ->len ] + match ->cost); } } return f[n] == INT_MAX / 2 ? -1 : f[n]; } };
欢迎关注和打赏,感谢支持!