leetcode weekly contest 406
100352. 交换后字典序最小的字符串
给你一个仅由数字组成的字符串 s,在最多交换一次 相邻 且具有相同 奇偶性 的数字后,返回可以得到的字典序最小的字符串。
如果两个数字都是奇数或都是偶数,则它们具有相同的奇偶性。例如,5 和 9、2 和 4 奇偶性相同,而 6 和 9 奇偶性不同。
示例 1:
输入: s = “45320”
输出: “43520”
解释:
s[1] == '5' 和 s[2] == '3' 都具有相同的奇偶性,交换它们可以得到字典序最小的字符串。
示例 2:
输入: s = “001”
输出: “001”
解释:
无需进行交换,因为 s 已经是字典序最小的。
提示:
2 <= s.length <= 100s仅由数字组成。
地址
题意
模拟
思路
- 直接模拟交换即可,选择前一个字符比后一个大的字符进行交换即可。
- 复杂度分析:
- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
代码
class Solution: |
100368. 从链表中移除在数组中存在的节点
给你一个整数数组 nums 和一个链表的头节点 head。从链表中移除所有存在于 nums 中的节点后,返回修改后的链表的头节点。
示例 1:
输入: nums = [1,2,3], head = [1,2,3,4,5]
输出: [4,5]
解释:

移除数值为 1, 2 和 3 的节点。
示例 2:
输入: nums = [1], head = [1,2,1,2,1,2]
输出: [2,2,2]
解释:

移除数值为 1 的节点。
示例 3:
输入: nums = [5], head = [1,2,3,4]
输出: [1,2,3,4]
解释:
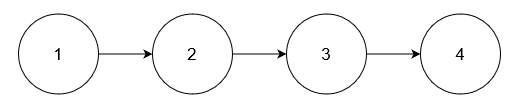
链表中不存在值为 5 的节点。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 105nums中的所有元素都是唯一的。- 链表中的节点数在
[1, 105]的范围内。 1 <= Node.val <= 105- 输入保证链表中至少有一个值没有在
nums中出现过。
地址
题意
模拟
思路
将数组中的元素从链表中删除即可
复杂度分析:
- 时间复杂度:$O(n + m)$,其中 $n$ 表示给定链表的长度。
- 空间复杂度:$O(m)$,其中 $m$ 表示给定的数组的长度
代码
class Solution: |
100361. 切蛋糕的最小总开销 I
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
horizontalCut的大小为m - 1,其中horizontalCut[i]表示沿着水平线i切蛋糕的开销。verticalCut的大小为n - 1,其中verticalCut[j]表示沿着垂直线j切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线
i切开蛋糕,开销为horizontalCut[i]。 - 沿着垂直线
j切开蛋糕,开销为verticalCut[j]。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:
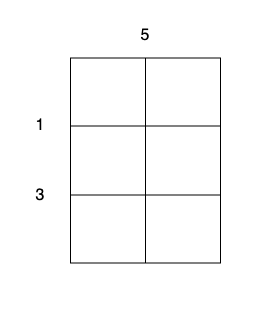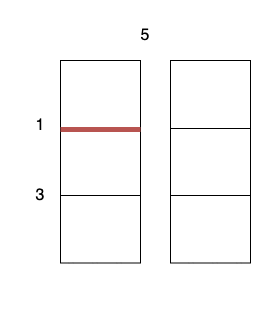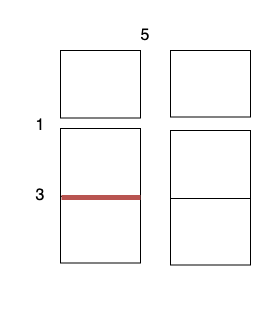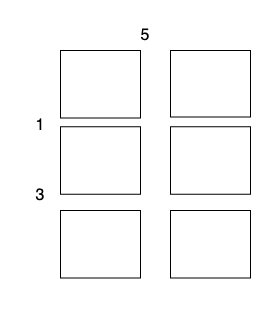
- 沿着垂直线 0 切开蛋糕,开销为 5 。
- 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。
示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
- 沿着水平线 0 切开蛋糕,开销为 7 。
- 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。 - 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。
提示:
1 <= m, n <= 20horizontalCut.length == m - 1verticalCut.length == n - 11 <= horizontalCut[i], verticalCut[i] <= 103
地址
https://leetcode.cn/contest/weekly-contest-406/problems/minimum-cost-for-cutting-cake-i/
题意
动态规划
思路
最简单的就是动态规划了, 设 $f(x_1,y_1,x_2,y_2)$ 表示以 $(x_1,y_1)$ 为左上顶点,以 $(x_2,y_2)$ 为右下顶点的矩形切割的最小代价,此时下一次切割我们要门水平切,要么竖直切,此时我们水平切或者竖直的话,可以得到以下递推公式:
$$
f(x_1,y_1,x_2,y_2) = \min(f(x_1, y_1, i, y_2) + f(i, y_1, x_2, y_2) + horizontalCut[i - 1]) \quad i \in(x_1 + 1, x_2-1)\
f(x_1,y_1,x_2,y_2) = \min(f(x_1, y_1, x_2, i) + f(x_1, i, x_2, y_2) + verticalCut[i - 1]) \quad i \in(y_1 + 1, y_2-1)
$$复杂度分析:
- 时间复杂度:$O(m^2n^2(m+n))$,其中 $mn$ 表示给定的 $m,n$;
- 空间复杂度:$O(m^2n^2)$,其中 $mn$ 表示给定的 $m,n$;
代码
class Solution: |
00367. 切蛋糕的最小总开销 II
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
horizontalCut的大小为m - 1,其中horizontalCut[i]表示沿着水平线i切蛋糕的开销。verticalCut的大小为n - 1,其中verticalCut[j]表示沿着垂直线j切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
- 沿着水平线
i切开蛋糕,开销为horizontalCut[i]。 - 沿着垂直线
j切开蛋糕,开销为verticalCut[j]。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
示例 1:
输入:m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]
输出:13
解释:

- 沿着垂直线 0 切开蛋糕,开销为 5 。
- 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 0 切开
3 x 1的蛋糕块,开销为 1 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。 - 沿着水平线 1 切开
2 x 1的蛋糕块,开销为 3 。
总开销为 5 + 1 + 1 + 3 + 3 = 13 。
示例 2:
输入:m = 2, n = 2, horizontalCut = [7], verticalCut = [4]
输出:15
解释:
- 沿着水平线 0 切开蛋糕,开销为 7 。
- 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。 - 沿着垂直线 0 切开
1 x 2的蛋糕块,开销为 4 。
总开销为 7 + 4 + 4 = 15 。
提示:
1 <= m, n <= 105horizontalCut.length == m - 1verticalCut.length == n - 11 <= horizontalCut[i], verticalCut[i] <= 103
地址
https://leetcode.cn/contest/weekly-contest-406/problems/minimum-cost-for-cutting-cake-ii/
题意
贪心
思路
- 假设当前已经再水平方向切成了 $x$ 块 ,竖直方向切成了 $y$ 块,此时如果当前选择水平切,则需要的代价为 $cost \times y$, 如果当前选择竖直切,则需要的代价为 $cost \times x$,实际比较我们发现越往后切的话,由于乘法倍数存在的原因,则此时需要的代价越大,因此根据贪心原则,此时单次切时代价越大切法应当即可能的提前切,单次切时代价越小的单位此时应该提前切,因此我们将所有代价按照从大到小进行排列,此时依次选择水平切或者竖直切,并统计当前再水平方向或者竖直方向已经切成的的块数即可。
- 复杂度分析:
- 时间复杂度:$O((m + n) \log (m + n)$,其中 $m,n$ 表示给的数;
- 空间复杂度:$O(m + n)$,其中 $m,n$ 表示给的数;
代码
class Solution: |
欢迎关注和打赏,感谢支持!
关注我的博客: https://mike-box.github.io/
关注我的微信公众号: 哪些奋斗者

扫描二维码,分享此文章
