leetcode biweekly contest 134
3206. 交替组 I
给你一个整数数组 colors ,它表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
colors[i] == 0表示第i块瓷砖的颜色是 红色 。colors[i] == 1表示第i块瓷砖的颜色是 蓝色 。
环中连续 3 块瓷砖的颜色如果是 交替 颜色(也就是说中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
输入:colors = [1,1,1]
输出:0
解释:
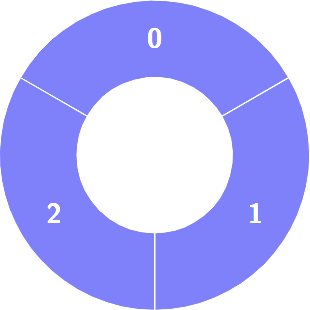
示例 2:
输入:colors = [0,1,0,0,1]
输出:3
解释:
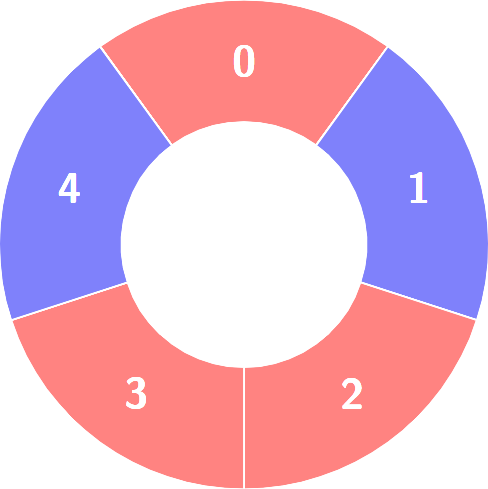
交替组包括:
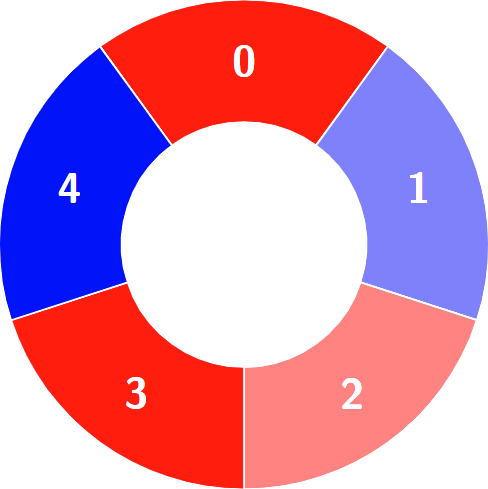
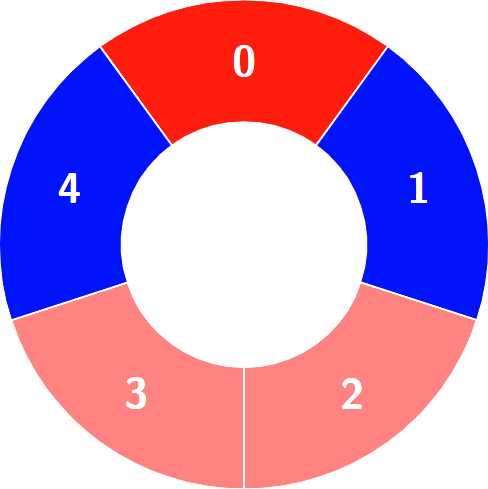
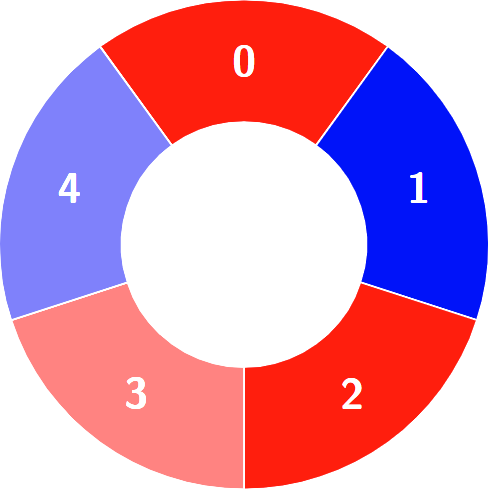
提示:
3 <= colors.length <= 1000 <= colors[i] <= 1
地址
https://leetcode.cn/contest/biweekly-contest-134/problems/alternating-groups-i/
题意
模拟相关
思路
- 直接模拟即可,检测连续三个相邻元素的元素是否相等即 $nums[i] \neq nums[(i - 1 + n) \mod n],nums[i] \neq nums[(i + 1) \mod n]$ 即可。
- 复杂度分析:
- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
代码
class Solution: |
3207. 与敌人战斗后的最大分数
给你一个下标从 0 开始的整数数组 enemyEnergies ,它表示一个下标从 0 开始的敌人能量数组。
同时给你一个整数 currentEnergy ,它表示你一开始拥有的能量值总量。
你一开始的分数为 0 ,且一开始所有的敌人都未标记。
你可以通过以下操作 之一 任意次(也可以 0 次)来得分:
选择一个
未标记
且满足
currentEnergy >= enemyEnergies[i]
的敌人
i
。在这个操作中:
- 你会获得
1分。 - 你的能量值减少
enemyEnergies[i],也就是说currentEnergy = currentEnergy - enemyEnergies[i]。
- 你会获得
如果你目前
至少
有
1
分,你可以选择一个
未标记
的敌人
i
。在这个操作中:
- 你的能量值增加
enemyEnergies[i],也就是说currentEnergy = currentEnergy + enemyEnergies[i]。 - 敌人
i被标记 。
- 你的能量值增加
请你返回通过以上操作,最多 可以获得多少分。
示例 1:
输入:enemyEnergies = [3,2,2], currentEnergy = 2
输出:3
解释:
通过以下操作可以得到最大得分 3 分:
- 对敌人 1 使用第一种操作:
points增加 1 ,currentEnergy减少 2 。所以points = 1且currentEnergy = 0。 - 对敌人 0 使用第二种操作:
currentEnergy增加 3 ,敌人 0 被标记。所以points = 1,currentEnergy = 3,被标记的敌人包括[0]。 - 对敌人 2 使用第一种操作:
points增加 1 ,currentEnergy减少 2 。所以points = 2且currentEnergy = 1,被标记的敌人包括[0]。 - 对敌人 2 使用第二种操作:
currentEnergy增加 2 ,敌人 2 被标记。所以points = 2,currentEnergy = 3且被标记的敌人包括[0, 2]。 - 对敌人 1 使用第一种操作:
points增加 1 ,currentEnergy减少 2 。所以points = 3,currentEnergy = 1,被标记的敌人包括[0, 2]。
示例 2:
输入:enemyEnergies = [2], currentEnergy = 10
输出:5
解释:
通过对敌人 0 进行第一种操作 5 次,得到最大得分。
提示:
1 <= enemyEnergies.length <= 1051 <= enemyEnergies[i] <= 1090 <= currentEnergy <= 109
地址
https://leetcode.cn/contest/biweekly-contest-134/problems/maximum-points-after-enemy-battles/
题意
贪心
思路
由于减少时,此时我们尽量减少元素最小的值,增加时我们尽量选择元素值最大的值即可,由于第一种操作可以对同一个元素操作无限次,因此我们在增加分数时,就选择第最小的元素来操作,增加能量时我们总是优先选择值最大的元素。
复杂度分析:
- 时间复杂度:$O(n \log n )$,其中 $n$ 表示给定数组的长度。
- 空间复杂度:$O(\log n)$,其中 $n$ 表示给定数组的长度。
代码
class Solution: |
3208. 交替组 II
给你一个整数数组 colors 和一个整数 k ,colors表示一个由红色和蓝色瓷砖组成的环,第 i 块瓷砖的颜色为 colors[i] :
colors[i] == 0表示第i块瓷砖的颜色是 红色 。colors[i] == 1表示第i块瓷砖的颜色是 蓝色 。
环中连续 k 块瓷砖的颜色如果是 交替 颜色(也就是说除了第一块和最后一块瓷砖以外,中间瓷砖的颜色与它 左边 和 右边 的颜色都不同),那么它被称为一个 交替 组。
请你返回 交替 组的数目。
注意 ,由于 colors 表示一个 环 ,第一块 瓷砖和 最后一块 瓷砖是相邻的。
示例 1:
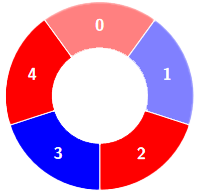
输入:colors = [0,1,0,1,0], k = 3
输出:3
解释:
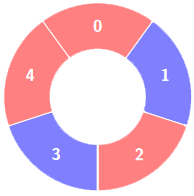
交替组包括:
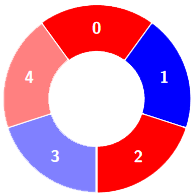
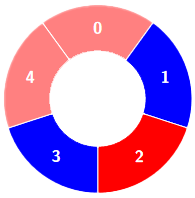
示例 2:
输入:colors = [0,1,0,0,1,0,1], k = 6
输出:2
解释:

交替组包括:


示例 3:
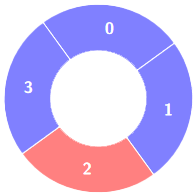
输入:colors = [1,1,0,1], k = 4
输出:0
解释:
提示:
3 <= colors.length <= 1050 <= colors[i] <= 13 <= k <= colors.length
地址
https://leetcode.cn/contest/biweekly-contest-134/problems/alternating-groups-ii/
题意
动态规划
思路
设 $dp[i]$ 表示以 $i$ 为结尾的最长交替组的长度,此时可以得到如下递推关系:
$$
dp[i] = dp[i - 1] + 1, \quad if colors[i] \neq colors[i-1] \
dp[i] = 1,\quad if colors[i] = colors[i-1] \
$$
此时如果以 $i$即为结尾的最长交替组的长度大于 $k$ ,则表示有一个新的长度为 $k$ 组出现,答案加 $1$ 即可,由于数组是循环数组,此时为了方便计算,我们此时直接在数组的后面添加前 $k-1$ 个元素即可。复杂度分析:
- 时间复杂度:$O(n+k )$,其中 $n$ 表示给定数组的长度,$k$ 表示给定的数字 $k$。
- 空间复杂度:$O(k)$,$k$ 表示给定的数字 $k$。
代码
class Solution: |
3209. 子数组按位与值为 K 的数目
给你一个整数数组 nums 和一个整数 k ,请你返回 nums 中有多少个子数组满足:子数组中所有元素按位 AND 的结果为 k 。
示例 1:
输入:nums = [1,1,1], k = 1
输出:6
解释:
所有子数组都只含有元素 1 。
示例 2:
输入:nums = [1,1,2], k = 1
输出:3
解释:
按位 AND 值为 1 的子数组包括:[**1**,1,2], [1,**1**,2], [**1,1**,2] 。
示例 3:
输入:nums = [1,2,3], k = 2
输出:2
解释:
按位 AND 值为 2 的子数组包括:[1,**2**,3], [1,**2,3**] 。
提示:
1 <= nums.length <= 1050 <= nums[i], k <= 109
地址
https://leetcode.cn/contest/biweekly-contest-134/problems/number-of-subarrays-with-and-value-of-k/
题意
双指针,动态规划
思路
- 首先我们需要知道一个结论 $x \and y \le x $, 即与的元素数目越多,值一定会变小的,这就决定了具有单调性,即 $f(i,j) = nums[i] \and nums[i + 1]\cdots\and nums[j] \le f(i,j+1) = nums[i] \and nums[i + 1]\cdots\and nums[j] \and nums[j+1]$,此时我们可以用二分查找即找 $f(l,j) >= k$ 的最小值 $l$,然后找到 $f(r,j) > k$ 的最小值 $r$,此时以 $j$ 为结尾且满足满足 $f(i,j) = k$ 的子数组数组即为 $r- l$ 个,此时我们再来讨论一下如何才能计算 $f(i,j)$,此时我们可以统计元素中每一位为 $0$ 的元素数目,一旦某一位出现 $0$,则这些元素与的结果是该位上一定为 $0$,即满足 $x \and 0 = 0$。
- $\text{add}(cnt,x)$: 此时表示统计元素 $x$ 中位上的 $0$ 的数目,并将其加入到统计数目中;
- $\text{del}(cnt,x)$: 此时表示去掉元素 $x$ 中位上的 $0$ 的数目,并将其从统计数目中去掉;
- $\text{get}(cnt)$: 此时表示计算当前元素与的结果,如果某位上 $0$ 的数目大于 $1$,则该位的结果上一定为 $0$;
- 动态规划,先说一个结论,$f(0,j),f(1,j),f(2,j), \cdots, f(j,j)$ 中不同元素的数目一定不超过 $\log nums[j]$ 个, 为啥是这样的结果
- 已知 $f(i,j) \ge f(i-1,j)$, 实际如果满足 $f(i,j) > f(i-1,j)$ 时,根据与的性质,此时 $f(i,j)$ 中的某一位上的 $1$ 经过与 $nums[j-1]$ 与后变为 $0$ 了,即至少减少某一位上的 $1$,由于 $f(i,j)$ 二进制位上最多只有 $\log nums[j]$ 个 $1$ ,因此最多减少 $\log nums[j]$ 个 $1$ 后,则元素变为了 $0$,
- 根据上诉推论,我们用 $dp[j-1]$ 保存 $f(0,j),f(1,j),f(2,j), \cdots, f(j,j)$ 的不同元素出现的次数,此时我们计算 $dp[i]$ 时,此时直接与 $dp[j-1]$ 中的每个元素进行与即可;
- 由于存在相同的元素,我们还需要保存每个元素出现的次数,此时以 $nums[i]$ 为结尾且结果等于 $k$ 的连续子数组数目即为 $dp[j][k]$;
- 非常经典的做法,当时最直接的办法还可线段树上无脑进行二分法,也是非常直接的办法了。
- 复杂度分析:
- 时间复杂度:$O(n \log U)$,其中 $n$ 表示给数组的长度,$U$ 表示元素中的最大值;
- 空间复杂度:$O(\log U)$,其中 $n$ 表示给数组的长度,$U$ 表示元素中的最大值;
代码
class Solution: |
欢迎关注和打赏,感谢支持!
关注我的博客: https://mike-box.github.io/
关注我的微信公众号: 哪些奋斗者

扫描二维码,分享此文章
