leetcode weekly contest 404

3200. 三角形的最大高度

给你两个整数 red 和 blue，分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形，满足第 1 行有 1 个球，第 2 行有 2 个球，第 3 行有 3 个球，依此类推。

每一行的球必须是相同颜色，且相邻行的颜色必须不同。

返回可以实现的三角形的最大高度。

示例 1：

输入： red = 2, blue = 4

输出： 3

解释：

上图显示了唯一可能的排列方式。

示例 2：

输入： red = 2, blue = 1

输出： 2

解释：

上图显示了唯一可能的排列方式。

示例 3：

输入： red = 1, blue = 1

输出： 1

示例 4：

输入： red = 10, blue = 1

输出： 2

解释：

上图显示了唯一可能的排列方式。

提示：

1 <= red, blue <= 100

地址

https://leetcode.cn/contest/weekly-contest-404/problems/maximum-height-of-a-triangle/

题意

模拟

思路

直接枚举行数即可，假设一共有 $i$ 行:
- 如果 $i$ 为奇数，则两种颜色数目分别为 $\dfrac{(i + 1) \times (i + 1)}{4}, \dfrac{(i + 1) \times i}{2} - \dfrac{(i + 1) \times (i + 1)}{4}$;
- 如果 $i$ 为偶数，则两种颜色数目分别为 $\dfrac{i \times i}{4}, \dfrac{(i + 1) \times i}{2} - \dfrac{i \times i}{4}$;
- 枚举 $i$ ,并检测给定的球的数目是否满足两种要求即可。
复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

代码

class Solution:
    def maxHeightOfTriangle(self, red: int, blue: int) -> int:
        a, b = 0, 0
        for i in range(100, -1, -1):
            tot = i * (i + 1) // 2
            if i & 1 == 1:
                a = (1 + i) * (i + 1) // 4
            else:
                a = i * i // 4
            b = tot - a
            if red >= a and blue >= b or red >= b and blue >= a:
                return i

        return 0

3201. 找出有效子序列的最大长度 I

给你一个整数数组 nums。

nums 的子序列 sub 的长度为 x ，如果其满足以下条件，则称其为 有效子序列：

(sub[0] + sub[1]) % 2 == (sub[1] + sub[2]) % 2 == ... == (sub[x - 2] + sub[x - 1]) % 2

返回 nums 的 最长的有效子序列 的长度。

一个 子序列 指的是从原数组中删除一些元素（也可以不删除任何元素），剩余元素保持原来顺序组成的新数组。

示例 1：

输入： nums = [1,2,3,4]

输出： 4

解释：

最长的有效子序列是 [1, 2, 3, 4]。

示例 2：

输入： nums = [1,2,1,1,2,1,2]

输出： 6

解释：

最长的有效子序列是 [1, 2, 1, 2, 1, 2]。

示例 3：

输入： nums = [1,3]

输出： 2

解释：

最长的有效子序列是 [1, 3]。

提示：

2 <= nums.length <= 2 * 105
1 <= nums[i] <= 107

地址

https://leetcode.cn/contest/weekly-contest-404/problems/find-the-maximum-length-of-valid-subsequence-i/

题意

动态规划

思路

与 t3 一样的思路，根据题意可以知道 $(a + b) \bmod k = (b + c) \bmod k$，此时可以得到 $a \bmod k + b \bmod k = b \bmod k + c\bmod k$, 等价于 $a \bmod k = c \bmod k$，此时我们一定可以得到如下：
- $sub[0] \bmod k = sub[2] \bmod k = sub[4] \bmod k, \cdots$;
- $sub[1] \bmod k = sub[3] \bmod k = sub[5] \bmod k, \cdots$;
此时我们只需要找到依次相邻且相等的最长序列即可，我们设 $dp[i][j]$ 表示最后一个数为 $i$，前一个数为 $j$ 子序列的最长长度，此时我们可以得到递推公式，假设当前元素为 $x$，此时可以得到 $dp[x \bmod k][i] = dp[i][x \bmod k] + 1$，特殊问题需要处理的时，假设当前遇到的元素为 $i$，$i$ 之前没有 $j$ 的时候该怎么处理，此时我们可以用一个标志位记录 $i$ 之前是否出现过 $j$ 即可，单独处理这类特殊情况即可，这样即可避免重复计算的问题。
复杂度分析：

时间复杂度：$O(nk )$，其中 $n$ 表示给定数组的长度，$k$ 表示给定的数字 $k$。
空间复杂度：$O(k^2)$，$k$ 表示给定的数字 $k$。

代码

class Solution {
public:
    int maximumLength(vector<int>& nums, int k) {
        int n = nums.size();
        vector<vector<int>> f(k, vector<int>(k));
        int res = 0;
        for (int x : nums) {
            int j = x % k;
            for (int i = 0; i < k; i++) {
                f[j][i] = 1 + f[i][j];
                res = max(res, f[j][i]);
            }           
        }
        return res;
    }
};

3202. 找出有效子序列的最大长度 II

给你一个整数数组 nums 和一个正整数 k 。

nums 的一个子序列 sub 的长度为 x ，如果其满足以下条件，则称其为 有效子序列 ：

(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == ... == (sub[x - 2] + sub[x - 1]) % k

返回 nums 的 最长****有效子序列 的长度。

示例 1：

输入：nums = [1,2,3,4,5], k = 2

输出：5

解释：

最长有效子序列是 [1, 2, 3, 4, 5] 。

示例 2：

输入：nums = [1,4,2,3,1,4], k = 3

输出：4

解释：

最长有效子序列是 [1, 4, 1, 4] 。

提示：

2 <= nums.length <= 103
1 <= nums[i] <= 107
1 <= k <= 103

地址

https://leetcode.cn/contest/weekly-contest-404/problems/find-the-maximum-length-of-valid-subsequence-ii/

题意

动态规划

思路

与 t3 一样的思路，根据题意可以知道 $(a + b) \bmod k = (b + c) \bmod k$，此时可以得到 $a \bmod k + b \bmod k = b \bmod k + c\bmod k$, 等价于 $a \bmod k = c \bmod k$，此时我们一定可以得到如下：
- $sub[0] \bmod k = sub[2] \bmod k = sub[4] \bmod k, \cdots$;
- $sub[1] \bmod k = sub[3] \bmod k = sub[5] \bmod k, \cdots$;
此时我们只需要找到依次相邻且相等的最长序列即可，我们设 $dp[i][j]$ 表示最后一个数为 $i$，前一个数为 $j$ 子序列的最长长度，此时我们可以得到递推公式，假设当前元素为 $x$，此时可以得到 $dp[x \bmod k][i] = dp[i][x \bmod k] + 1$，特殊问题需要处理的时，假设当前遇到的元素为 $i$，$i$ 之前没有 $j$ 的时候该怎么处理，此时我们可以用一个标志位记录 $i$ 之前是否出现过 $j$ 即可，单独处理这类特殊情况即可，这样即可避免重复计算的问题。
另一种解法，可以参考枚举余数，考察子序列的最后一项, 假设子数组相邻两项对 $k$ 取模的结果为 $m$，此时假设已知第一项对 $k$ 取模的结果为 $x$，此时第二项对 $k$ 取模的结果即为 $(m - x + k) \bmod k$, 此时我们维护一个数组 $f$，其中 $f[x]$ 表示最后一项对 $k$ 取模的结果为 $x$ 的最长子序列的长度，假设当前的元素为 $y$，此时它前一个元素与 $k$ 取模的结果一定为 $(m - y \bmod k + k) \bmod k$ ，此时可以得到递推公式为 $f[x] = f[(m - x + k) \bmod k] + 1$.
复杂度分析：

时间复杂度：$O(nk )$，其中 $n$ 表示给定数组的长度，$k$ 表示给定的数字 $k$。
空间复杂度：$O(k^2)$，$k$ 表示给定的数字 $k$。

代码

class Solution {
public:
    int maximumLength(vector<int>& nums, int k) {
        int n = nums.size();
        vector<vector<int>> dp(k, vector<int>(k));
        vector<bool> visit(k);
        int res = 0;
        for (int x : nums) {
            int j = x % k;
            for (int i = 0; i < k; i++) {
                if (i == j) {
                    dp[i][j]++;
                } else {
                    if (visit[i] && dp[j][i] == 0) {
                        dp[j][i] = 2;
                    }
                    if (dp[i][j] > 0) {
                        dp[j][i] = 1 + dp[i][j];
                    }
                }
                res = max(res, dp[j][i]);
            }           
            visit[j] = true;
        }
        return res;
    }
};

class Solution {
public:
    int maximumLength(vector<int>& nums, int k) {
        int res = 0;
        for (int i = 0; i < k; i++) {
            vector<int> f(k);
            for (int x : nums) {
                int j = x % k;
                f[j] = f[(i - j + k) % k] + 1;
                res = max(res, f[j]);
            }
        }
        return res;
    }
};

3203. 合并两棵树后的最小直径

给你两棵无向树，分别有 n 和 m 个节点，节点编号分别为 0 到 n - 1 和 0 到 m - 1 。给你两个二维整数数组 edges1 和 edges2 ，长度分别为 n - 1 和 m - 1 ，其中 edges1[i] = [ai, bi] 表示在第一棵树中节点 ai 和 bi 之间有一条边，edges2[i] = [ui, vi] 表示在第二棵树中节点 ui 和 vi 之间有一条边。

你必须在第一棵树和第二棵树中分别选一个节点，并用一条边连接它们。

请你返回添加边后得到的树中，最小直径 为多少。

一棵树的直径指的是树中任意两个节点之间的最长路径长度。

示例 1：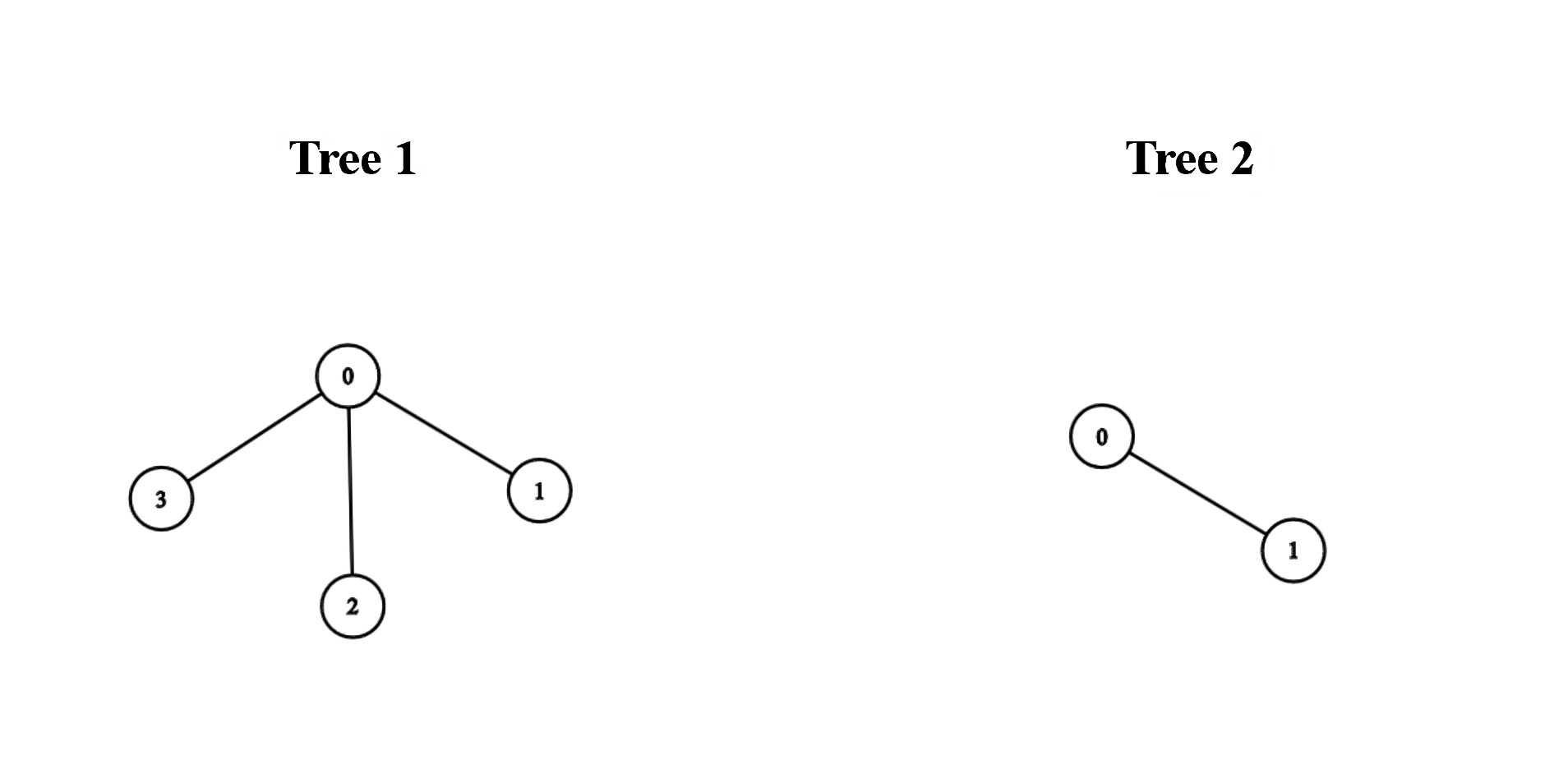

输入：edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]

输出：3

解释：

将第一棵树中的节点 0 与第二棵树中的任意节点连接，得到一棵直径为 3 得树。

示例 2：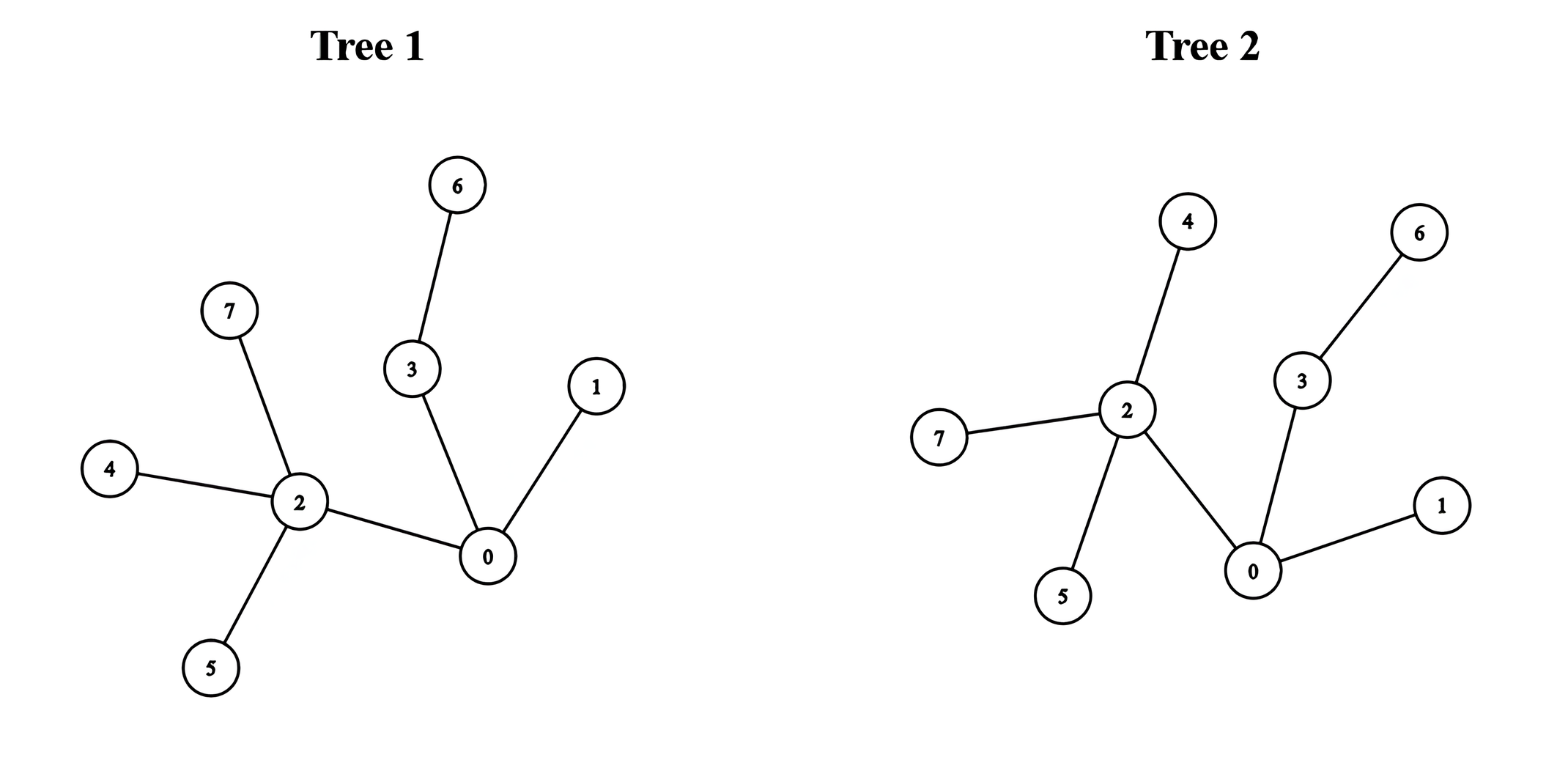

输入：edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]

输出：5

解释：

将第一棵树中的节点 0 和第二棵树中的节点 0 连接，可以得到一棵直径为 5 的树。

提示：

1 <= n, m <= 105
edges1.length == n - 1
edges2.length == m - 1
edges1[i].length == edges2[i].length == 2
edges1[i] = [ai, bi]
0 <= ai, bi < n
edges2[i] = [ui, vi]
0 <= ui, vi < m
输入保证 edges1 和 edges2 分别表示一棵合法的树。

地址

https://leetcode.cn/contest/weekly-contest-404/problems/find-minimum-diameter-after-merging-two-trees/

题意

树

思路

题目本身不是很难，难点在于树的直径的求法，可以参考树的直径，此时我们可以用两次 $dfs$ 或者 $bfs$ 即可，找到最远的距离即为树的直径，回到问题本身，题目要求合并后的直径尽可能的小，根据结论可以知道：
- 两棵树合并后，新直径的两个端点，一定是原来两棵树直径的四个端点里的其中两个。
- 假设我们选择了第一个树的点 $x$ 与第二个树的点 $y$ 进行相连，此时新的树的直径分为以下三种情况:
  - 要么为第一个树的直径 $d_1$;
  - 要么为第二个树的直径 $d_2$;
  - 要么为通过 $x-y$ 这条边相连的某个路径，假设此时最长的路径为 $a-x-y-b$，其中 $a,x$ 属于第一个树，$y,b$ 属于第二个树，经分析可以知道 $a,b$ 一定为叶子节点，此时我们需要使得 $a-x$ 与 $y-b$ 这两条边尽可能的小，即我们找到在第一个树中找到一个点 $x$ 使得树中其余的点到 $x$ 的最大距离尽可能的小，同理找到 $y$ 使得数中剩余的点到 $y$ 的最大距离尽可能的小，根据直径的定义，最优选择是选择直径的最中间的两个点相连。
  - 我们可以用反证法证明，任意点到达 $x$ 的最小的最大距离一定是 $\dfrac{d_1 + 1}{2}$,任意点到达 $y$ 的最小的最大距离一定是 $\dfrac{d_2 + 1}{2}$,否则就违反了直径的定义；
  - 此时最终的返回结果即为 $\max(d_1, d_2,\dfrac{d_1 + 1}{2} + \dfrac{d_2 + 1}{2} + 1)$;
复杂度分析：

时间复杂度：$O(n + m)$，其中 $n,m$ 表示给定树的结点数目;
空间复杂度：$O(n + m)$，其中 $n,m$ 表示给定树的结点数目;

代码

class Solution {
public:
    int minimumDiameterAfterMerge(vector<vector<int>>& edges1, vector<vector<int>>& edges2) {
        int d1 = bfs(edges1);
        int d2 = bfs(edges2);
        return max({d1, d2, (d1 + 1) / 2 + (d2 + 1) / 2 + 1});
    }
    
    int bfs(vector<vector<int>>& edges1) {
        int n = edges1.size() + 1;
        vector<vector<int>> graph(n);
        vector<bool> visit(n, false);
        queue<int> q;
        int last = -1;
        q.emplace(0);
        visit[0] = true;
        
        for (auto e : edges1) {
            graph[e[0]].emplace_back(e[1]);
            graph[e[1]].emplace_back(e[0]);
        }
        
        while (!q.empty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int curr = q.front();
                q.pop();
                last = curr;
                for (auto v : graph[curr]) {
                    if (visit[v]) continue;
                    q.emplace(v);
                    visit[v] = true;
                }
            }
        }
        
        for (int i = 0; i < n; i++) {
            visit[i] = false;
        }
        q.emplace(last);
        int dist = -1;
        visit[last] = true;
        while (!q.empty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int curr = q.front();
                q.pop();
                for (auto v : graph[curr]) {
                    if (visit[v]) continue;
                    q.emplace(v);
                    visit[v] = true;
                }
            }
            dist++;
        }
        
        return dist;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 哪些奋斗者

Tags: 题解力扣周赛赛

← leetcode biweekly contest 133 leetcode weekly contest 403 →

扫描二维码，分享此文章