leetcode weekly contest 403

3194. 最小元素和最大元素的最小平均值

你有一个初始为空的浮点数数组 averages。另给你一个包含 n 个整数的数组 nums，其中 n 为偶数。

你需要重复以下步骤 n / 2 次：

• 从 nums 中移除 最小 的元素 minElement 和 最大 的元素 maxElement。
• 将 (minElement + maxElement) / 2 加入到 averages 中。

返回 averages 中的 最小 元素。

示例 1：

输入： nums = [7,8,3,4,15,13,4,1]

输出： 5.5

解释：

返回 averages 中最小的元素，即 5.5。

示例 2：

输入： nums = [1,9,8,3,10,5]

输出： 5.5

解释：

示例 3：

输入： nums = [1,2,3,7,8,9]

输出： 5.0

解释：

提示：

• 2 <= n == nums.length <= 50
• n 为偶数。
• 1 <= nums[i] <= 50

地址

https://leetcode.cn/contest/weekly-contest-403/problems/minimum-average-of-smallest-and-largest-elements/

题意

直接模拟

思路

1. 排序后每次取最大值与最小值，并求平均数。
2. 复杂度分析：

• 时间复杂度：$O(n \log n)$。
• 空间复杂度：$O(\log n)$。

代码

class Solution:
    def minimumAverage(self, nums: List[int]) -> float:
        nums.sort()
        return min([(nums[i] + nums[-1-i]) / 2 for i in range(len(nums) // 2)])

3195. 包含所有 1 的最小矩形面积 I

显示英文描述

我的提交返回竞赛

• 通过的用户数2376
• 尝试过的用户数2432
• 用户总通过次数2427
• 用户总提交次数3055
• 题目难度****Medium

给你一个二维 二进制 数组 grid。请你找出一个边在水平方向和竖直方向上、面积 最小 的矩形，并且满足 grid 中所有的 1 都在矩形的内部。

返回这个矩形可能的 最小 面积。

示例 1：

输入： grid = [[0,1,0],[1,0,1]]

输出： 6

解释：

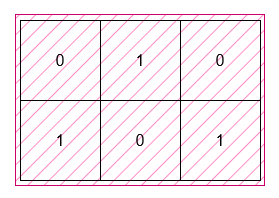
这个最小矩形的高度为 2，宽度为 3，因此面积为 2 * 3 = 6。

示例 2：

输入： grid = [[0,0],[1,0]]

输出： 1

解释：

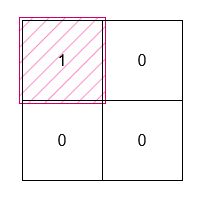
这个最小矩形的高度和宽度都是 1，因此面积为 1 * 1 = 1。

提示：

• 1 <= grid.length, grid[i].length <= 1000
• grid[i][j] 是 0 或 1。
• 输入保证 grid 中至少有一个 1 。

地址

https://leetcode.cn/contest/weekly-contest-403/problems/find-the-minimum-area-to-cover-all-ones-i/

题意

直接模拟

思路

1. 找到矩形的左右上下的边缘即可，然后返回面积即可。
2. 复杂度分析：

• 时间复杂度：$O(mn )$，其中 $mn$ 表示给定矩阵的长与宽。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def minimumArea(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        left, right = m, 0
        top, down = n, 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    left = min(left, j)
                    right = max(right, j)
                    top = min(top, i)
                    down = max(top, i)
                    
        return (right - left + 1) * (down - top + 1)

3196. 最大化子数组的总成本

给你一个长度为 n 的整数数组 nums。

子数组 nums[l..r]（其中 0 <= l <= r < n）的 成本 定义为：

cost(l, r) = nums[l] - nums[l + 1] + ... + nums[r] * (−1)r − l

你的任务是将 nums 分割成若干子数组，使得所有子数组的成本之和 最大化，并确保每个元素 正好 属于一个子数组。

具体来说，如果 nums 被分割成 k 个子数组，且分割点为索引 i1, i2, ..., ik − 1（其中 0 <= i1 < i2 < ... < ik - 1 < n - 1），则总成本为：

cost(0, i1) + cost(i1 + 1, i2) + ... + cost(ik − 1 + 1, n − 1)

返回在最优分割方式下的子数组成本之和的最大值。

注意：如果 nums 没有被分割，即 k = 1，则总成本即为 cost(0, n - 1)。

示例 1：

输入： nums = [1,-2,3,4]

输出： 10

解释：

一种总成本最大化的方法是将 [1, -2, 3, 4] 分割成子数组 [1, -2, 3] 和 [4]。总成本为 (1 + 2 + 3) + 4 = 10。

示例 2：

输入： nums = [1,-1,1,-1]

输出： 4

解释：

一种总成本最大化的方法是将 [1, -1, 1, -1] 分割成子数组 [1, -1] 和 [1, -1]。总成本为 (1 + 1) + (1 + 1) = 4。

示例 3：

输入： nums = [0]

输出： 0

解释：

无法进一步分割数组，因此答案为 0。

示例 4：

输入： nums = [1,-1]

输出： 2

解释：

选择整个数组，总成本为 1 + 1 = 2，这是可能的最大成本。

提示：

• 1 <= nums.length <= 105
• -109 <= nums[i] <= 109

地址

https://leetcode.cn/contest/weekly-contest-403/problems/maximize-total-cost-of-alternating-subarrays/

题意

动态规划

思路

1. 我们仔细观察一下，由于每个子数组中的 $1,-1$都是交替出现的，且子数组的第一个元素必须为 $1$，此时观察发现相邻两个元素符号分布规律如下：

   • $1, -1$;
   • $1,1$;
   • $-1,1$;
   • 一定不存在两个 $-1$ 情形；

2. 设 $dp[i][0]$ 表示第 $i$ 个元素乘以 $1$ 为结尾时的最大值， 设 $dp[i][1]$ 表示第 $i$ 个元素乘以 $-1$ 为结尾时的最大值， 此时我们可以得到递推公式如下：

   $$dp[i][0] = \max(dp[i-1][0],dp[i-1][1]) + nums[i], dp[i][1] = dp[i-1][0] - nums[i]$$

   我们按照上述递推公式进行推理即可。

3. 复杂度：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度；
• 空间复杂度：$O(1)$；

代码

class Solution:
    def maximumTotalCost(self, nums: List[int]) -> int:
        dp = [[0] * 2 for _ in range(len(nums))]
        dp[0][0] = nums[0]
        dp[0][1] = -inf
        for i, x in enumerate(nums[1:]):
            dp[i + 1][0] = max(dp[i][1] + x, dp[i][0] + x)
            dp[i + 1][1] = dp[i][0] - x
        return max(dp[-1])

3197. 包含所有 1 的最小矩形面积 II

给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形，并且满足 grid 中所有的 1 都在这些矩形的内部。

返回这些矩形面积之和的 最小 可能值。

注意，这些矩形可以相接。

示例 1：

输入： grid = [[1,0,1],[1,1,1]]

输出： 5

解释：

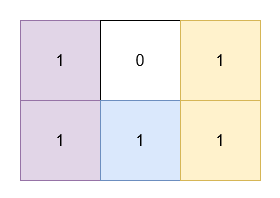
• 位于 (0, 0) 和 (1, 0) 的 1 被一个面积为 2 的矩形覆盖。
• 位于 (0, 2) 和 (1, 2) 的 1 被一个面积为 2 的矩形覆盖。
• 位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。

示例 2：

输入： grid = [[1,0,1,0],[0,1,0,1]]

输出： 5

解释：

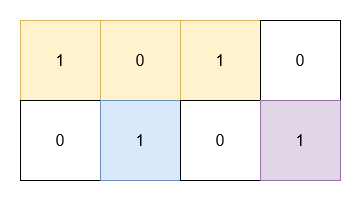
• 位于 (0, 0) 和 (0, 2) 的 1 被一个面积为 3 的矩形覆盖。
• 位于 (1, 1) 的 1 被一个面积为 1 的矩形覆盖。
• 位于 (1, 3) 的 1 被一个面积为 1 的矩形覆盖。

提示：

• 1 <= grid.length, grid[i].length <= 30
• grid[i][j] 是 0 或 1。
• 输入保证 grid 中至少有三个 1 。

地址

https://leetcode.cn/contest/biweekly-contest-133/problems/count-the-number-of-inversions/

题意

枚举

思路

1. 根据分析实际上将矩形分为三个矩形的情形如下，共有 $6$ 种情况，分别枚举便利即可。

2. 我们设函数 $get(x, y, h, w)$ 表示当前矩形矩形中左上顶点为 $(x,y)$，此时矩形的高为 $h$，宽度为 $w$ 时，此时覆盖该矩形区域中 $1$ 的最小矩形面积，分类讨论如下：

   • 第一类情形：枚举分割为第 $i,j$ 行，此时可以得到需要的矩形面积为：

     $get(0, 0, i, n) + get(i, 0, j - i, n) + get(j, 0, m - j, n)$;

   • 第二类情形：枚举分割为第 $i,j$ 列，此时可以得到需要的矩形面积为：$get(0, 0, m, i) + get(0, i, m, j - i) + get(0, j, m, n - j)$;

   • 第三类情形：枚举中间的分割点 $(x,y)$，此时可以得到需要的矩形面积为：$get(0, 0, m, j) + get(0, j, i, n - j) + get(i, j, m - i, n - j)$;

   • 第四类情形：枚举中间的分割点 $(x,y)$，此时可以得到需要的矩形面积为：$get(0, 0, i, j) + get(i, 0, m - i, j) + get(0, j, m, n - j)$;

   • 第五类情形：枚举中间的分割点 $(x,y)$，此时可以得到需要的矩形面积为：$get(0, 0, i, n) + get(i, 0, m - i, j) + get(i, j, m - i, n - j)$;

   • 第六类情形：枚举中间的分割点 $(x,y)$，此时可以得到需要的矩形面积为：$get(0, 0, i, j) + get(0, j, i, n - j) + get(i, 0, m - i, n)$;

   • 求出以上流泪情形的最小值返回即可，题目反而成为一个中等题目；

3. 复杂度分析：

• 时间复杂度：$O(m^2n^2)$，其中 $m,n$ 表示给定矩形的长与宽，当然可以用二分查找继续优化，时间复杂度可以优化到 $O(mn\times(m \log n + n \log m))$;
• 空间复杂度：$O(mn)$，其中 $m,n$ 表示给定矩形的长与宽，

代码

class Solution {
public:
    int minimumSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> rows(m);
        vector<vector<int>> cols(n);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    rows[i].emplace_back(j);
                    cols[j].emplace_back(i);
                }
            }
        }

        auto get = [&](int x, int y, int h, int w) {
            int left = n, right = -1;
            int top = m, down = -1;
            for (int i = x; i < x + h; i++) {
                int a = lower_bound(rows[i].begin(), rows[i].end(), y) - rows[i].begin();
                int b = lower_bound(rows[i].begin(), rows[i].end(), y + w) - rows[i].begin();
                if (b > a) {
                    left = min(left, rows[i][a]);
                    right = max(right, rows[i][b - 1]);
                }
            }
            for (int i = y; i < y + w; i++) {
                int a = lower_bound(cols[i].begin(), cols[i].end(), x) - cols[i].begin();
                int b = lower_bound(cols[i].begin(), cols[i].end(), x + h) - cols[i].begin();
                if (b > a) {
                    top = min(top, cols[i][a]);
                    down = max(down, cols[i][b - 1]);
                }
            }
            if (right >= 0 && down >= 0) {
                return (right - left + 1) * (down - top + 1);
            } else {
                return 0;
            }
        };

        int res = m * n;
        for (int i = 1; i < m; i++) {
            for (int j = i + 1; j < m; j++) {
                res = min(res, get(0, 0, i, n) + get(i, 0, j - i, n) + get(j, 0, m - j, n));
            }
        }
        for (int i = 1; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                res = min(res, get(0, 0, m, i) + get(0, i, m, j - i) + get(0, j, m, n - j));
            }
        }
        for (int i = 1; i <= m - 1; i++) {
            for (int j = 1; j <= n - 1; j++) {
                res = min(res, get(0, 0, m, j) + get(0, j, i, n - j) + get(i, j, m - i, n - j));
                res = min(res, get(0, 0, i, j) + get(i, 0, m - i, j) + get(0, j, m, n - j));
                res = min(res, get(0, 0, i, n) + get(i, 0, m - i, j) + get(i, j, m - i, n - j));
                res = min(res, get(0, 0, i, j) + get(0, j, i, n - j) + get(i, 0, m - i, n));
            }
        }
        return res;
    }
};

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu

• 关注我的微信公众号: 哪些奋斗者