leetcode weekly contest 397

t4 又是一个比较难的题目。

3146. 两个字符串的排列差

给你两个字符串 s 和 t，每个字符串中的字符都不重复，且 t 是 s 的一个排列。

排列差 定义为 s 和 t 中每个字符在两个字符串中位置的绝对差值之和。

返回 s 和 t 之间的 排列差 。

示例 1：

输入：s = “abc”, t = “bac”

输出：2

解释：

对于 s = "abc" 和 t = "bac"，排列差是：

• "a" 在 s 中的位置与在 t 中的位置之差的绝对值。
• "b" 在 s 中的位置与在 t 中的位置之差的绝对值。
• "c" 在 s 中的位置与在 t 中的位置之差的绝对值。

即，s 和 t 的排列差等于 |0 - 1| + |2 - 2| + |1 - 0| = 2。

示例 2：

输入：s = “abcde”, t = “edbac”

输出：12

解释： s 和 t 的排列差等于 |0 - 3| + |1 - 2| + |2 - 4| + |3 - 1| + |4 - 0| = 12。

提示：

• 1 <= s.length <= 26
• 每个字符在 s 中最多出现一次。
• t 是 s 的一个排列。
• s 仅由小写英文字母组成。

地址

https://leetcode.cn/contest/weekly-contest-397/problems/permutation-difference-between-two-strings/

题意

直接模拟

思路

1. 直接模拟即可，每个字符的索引进行相减即可。
2. 复杂度分析：

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def findPermutationDifference(self, s: str, t: str) -> int:
        cnt1 = [0] * 26
        cnt2 = [0] * 26
        for i, ch in enumerate(s):
            cnt1[ord(ch) - ord('a')] = i
        for i, ch in enumerate(t):
            cnt2[ord(ch) - ord('a')] = i;
        return sum(abs(cnt1[i] - cnt2[i]) for i in range(26))

impl Solution {
    pub fn find_permutation_difference(s: String, t: String) -> i32 {
        let mut cnt1 = vec![0; 26];
        let mut cnt2 = vec![0; 26];
        for (i, ch) in s.chars().enumerate() {
            cnt1[(ch as usize - 'a' as usize)] = i as i32;
        }
        for (i, ch) in t.chars().enumerate() {
            cnt2[(ch as usize - 'a' as usize)] = i as i32;
        }
        (0..26).map(|i| (cnt1[i] - cnt2[i]).abs()).sum()
    }
}

3147. 从魔法师身上吸取的最大能量

在神秘的地牢中，n 个魔法师站成一排。每个魔法师都拥有一个属性，这个属性可以给你提供能量。有些魔法师可能会给你负能量，即从你身上吸取能量。

你被施加了一种诅咒，当你从魔法师 i 处吸收能量后，你将被立即传送到魔法师 (i + k) 处。这一过程将重复进行，直到你到达一个不存在 (i + k) 的魔法师为止。

换句话说，你将选择一个起点，然后以 k 为间隔跳跃，直到到达魔法师序列的末端，在过程中吸收所有的能量。

给定一个数组 energy 和一个整数k，返回你能获得的 最大 能量。

示例 1：

输入： energy = [5,2,-10,-5,1], k = 3

输出： 3

解释：可以从魔法师 1 开始，吸收能量 2 + 1 = 3。

示例 2：

输入： energy = [-2,-3,-1], k = 2

输出： -1

解释：可以从魔法师 2 开始，吸收能量 -1。

提示：

• 1 <= energy.length <= 105
• -1000 <= energy[i] <= 1000
• 1 <= k <= energy.length - 1

地址

https://leetcode.cn/contest/weekly-contest-397/problems/taking-maximum-energy-from-the-mystic-dungeon/

题意

前缀和

思路

1. 我们可以观察到一个问题，一旦某个从某个位置 $i$ 开始吸取时，此时它可以吸取的能量一定是确定的，它吸取的能量即为 $energy[i],energy [i + k], energy [i + 2k], \cdots,energy[x]$。此时我们自然而然想到了前缀和，记录从 $i$ 开始每隔 $k$ 个位置的元素的前缀和，此时就可以求出每个位置中可以汲取的最大能量。
2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。
• 空间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。

代码

impl Solution {
    pub fn maximum_energy(energy: Vec<i32>, k: i32) -> i32 {
        let n = energy.len();
        let mut res = std::i32::MIN;

        for i in 0..k {
            let mut psum = vec![0];
            let mut tot = 0;
            for j in (i..n as i32).step_by(k as usize) {
                tot += energy[j as usize];
                psum.push(tot);
            }
            for j in 1..psum.len() {
                res = res.max(psum[psum.len() - 1] - psum[j - 1]);
            }
        }
        res
    }
}

class Solution:
    def maximumEnergy(self, energy: List[int], k: int) -> int:
        n = len(energy)
        res = -inf
        for i in range(k):
            psum = [0]
            tot = 0
            for j in range(i, n, k):
                tot += energy[j]
                psum.append(tot)
            for j in range(1, len(psum)):
                res = max(res, psum[-1] - psum[j - 1])
        return res;

3148. 矩阵中的最大得分

给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格（不必相邻）。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。

你可以从 任一 单元格开始，并且必须至少移动一次。

返回你能得到的 最大 总得分。

示例 1：

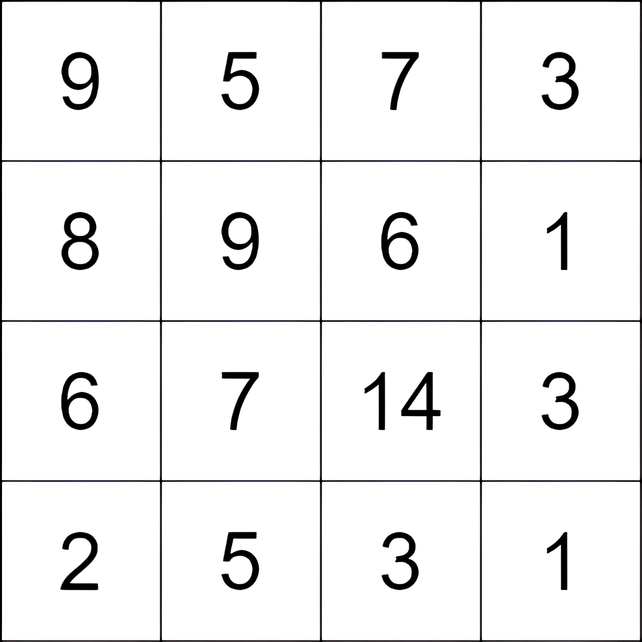
输入：grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

输出：9

解释：从单元格 (0, 1) 开始，并执行以下移动：
- 从单元格 (0, 1) 移动到 (2, 1)，得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2)，得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。

示例 2：

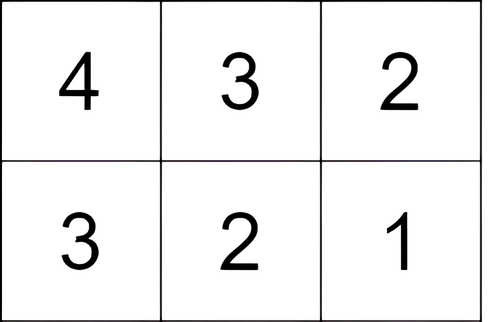
输入：grid = [[4,3,2],[3,2,1]]

输出：-1

解释：从单元格 (0, 0) 开始，执行一次移动：从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 105

地址

https://leetcode.cn/contest/weekly-contest-397/problems/maximum-difference-score-in-a-grid/

题意

动态规划

思路

1. 假设我们移动的轨迹为 $c_1,c_2,c_3,\cdots,c_m$，此时每次的得分分别为 $c_2 - c_1,c_3-c_2, \cdots,c_m -c_{m-1}$, 将这些得分加起来的和即为 $c_m - c_1$，即位置 $(i,j)$ 移动到所有满足 $(i’,j’), i’ \ge i, j \ge j$ 时满足 $grid[i’][j’]-grid[i][j]$ 的最大值，反过来给定 $(i’,j’)$, 找到所有满足 $(i,j),i’ \ge i, j \ge j$ 时的 $grid[i’][j’]-grid[i][j]$ 的最大值，此时我们找到 $(i,j),i’ \ge i, j \ge j$ 的最小值即可。

2. 复杂度：

• 时间复杂度：$O(n^2)$，其中 $n$ 表示给定的字符串的长度；
• 空间复杂度：$O(n)$；

代码

class Solution:
    def maxScore(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dp = [row[:] for row in grid]
        res = -inf
        for i in range(0, m):
            for j in range(0, n):
                if i > 0:
                    res = max(res, grid[i][j] - dp[i - 1][j])
                    dp[i][j] = min(dp[i][j], dp[i - 1][j])
                if j > 0:
                    res = max(res, grid[i][j] - dp[i][j - 1])
                    dp[i][j] = min(dp[i][j], dp[i][j - 1])
        return res

3149. 找出分数最低的排列

给你一个数组 nums ，它是 [0, 1, 2, ..., n - 1] 的一个排列 。对于任意一个 [0, 1, 2, ..., n - 1] 的排列 perm ，其 分数 定义为：

score(perm) = |perm[0] - nums[perm[1]]| + |perm[1] - nums[perm[2]]| + ... + |perm[n - 1] - nums[perm[0]]|

返回具有 最低 分数的排列 perm 。如果存在多个满足题意且分数相等的排列，则返回其中字典序最小的一个。

示例 1：

输入：nums = [1,0,2]

输出：[0,1,2]

解释：

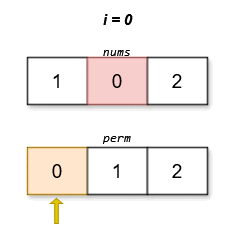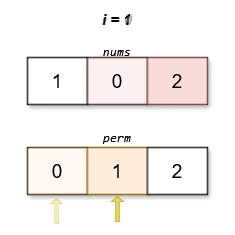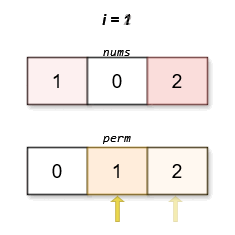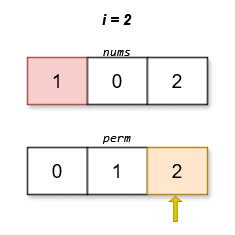
字典序最小且分数最低的排列是 [0,1,2]。这个排列的分数是 |0 - 0| + |1 - 2| + |2 - 1| = 2 。

示例 2：

输入：nums = [0,2,1]

输出：[0,2,1]

解释：

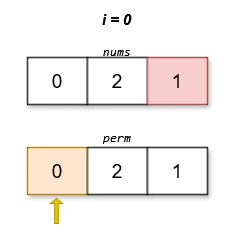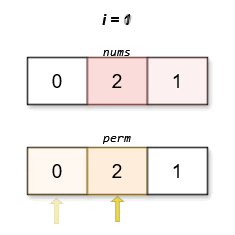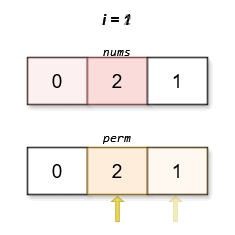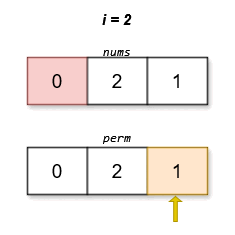
字典序最小且分数最低的排列是 [0,2,1]。这个排列的分数是 |0 - 1| + |2 - 2| + |1 - 0| = 2 。

提示：

• 2 <= n == nums.length <= 14
• nums 是 [0, 1, 2, ..., n - 1] 的一个排列。

地址

https://leetcode.cn/contest/weekly-contest-397/problems/find-the-minimum-cost-array-permutation/

题意

状态压缩dp，记忆化搜索

思路

1. 比较经典的动态规划，设 $memo[mask][i]$ 表示当前选择的元素为 $mask$ 且最后选择的元素为 $i$，题目关键在于第一个元素一定选择 $0$，然后就是常规的动态规划了。
2. 复杂度分析：

• 时间复杂度：$O(n \times 2^n)$，其中 $n$ 表示给数组的长度;
• 空间复杂度：$O(2^n)$，其中 $n$ 表示给数组的长度;

代码

class Solution {
public:
    vector<int> findPermutation(vector<int>& nums) {
        int n = nums.size();
        vector<int> ans;
        vector<vector<int>> memo(1 << n, vector<int>(n, -1));
        
        function<int(int, int)> dfs = [&](int mask, int i) -> int {
            if (mask == (1 << n) - 1) {
                memo[mask][i] = abs(i - nums[0]);
                return abs(i - nums[0]);
            }
            if (memo[mask][i] != -1) {
                return memo[mask][i];
            }
            int res = INT_MAX;
            for (int j = 1; j < n; j++) {
                if ((mask & (1 << j)) == 0) {
                    res = min(res, dfs(mask | (1 << j), j) + abs(i - nums[j]));
                }
            }
            memo[mask][i] = res;
            return res;
        };
        function<void(int, int)> make = [&](int mask, int i) {
            ans.push_back(i);
            if (mask == (1 << n) - 1) {
                return;
            }
            for (int j = 1; j < n; j++) {
                if ((mask & (1 << j)) == 0 && memo[mask][i] == memo[mask | (1 << j)][j] + abs(i - nums[j])) {
                    make(mask | (1 << j), j);
                    break;
                }
            }
        };
        
        dfs(1, 0);
        make(1, 0);
        return ans;
    }
};

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu

• 关注我的微信公众号: 哪些奋斗者