leetcode biweekly contest 131

t4 又是线段树类的数学题目。

3158. 求出出现两次数字的 XOR 值

给你一个数组 nums ，数组中的数字要么出现一次，要么出现两次。

请你返回数组中所有出现两次数字的按位 XOR 值，如果没有数字出现过两次，返回 0 。

示例 1：

输入：nums = [1,2,1,3]

输出：1

解释：

nums 中唯一出现过两次的数字是 1 。

示例 2：

输入：nums = [1,2,3]

输出：0

解释：

nums 中没有数字出现两次。

示例 3：

输入：nums = [1,2,2,1]

输出：3

解释：

数字 1 和 2 出现过两次。1 XOR 2 == 3 。

提示：

1 <= nums.length <= 50
1 <= nums[i] <= 50
nums 中每个数字要么出现过一次，要么出现过两次。

地址

https://leetcode.cn/contest/biweekly-contest-131/problems/find-the-xor-of-numbers-which-appear-twice/

题意

统计，排序

思路

哈希统计或者排序均可，对所有出现 $2$ 次元素进行异或。
复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

代码

class Solution:
    def duplicateNumbersXOR(self, nums: List[int]) -> int:
        nums.sort()
        res = 0
        for i in range(1, len(nums)):
            if nums[i] == nums[i - 1]:
                res ^= nums[i - 1]
        return res

impl Solution {
    pub fn duplicate_numbers_xor(nums: Vec<i32>) -> i32 {
        let mut nums = nums;
        nums.sort();
        let mut res = 0;
        for i in 1..nums.len() {
            if nums[i] == nums[i - 1] {
                res ^= nums[i - 1];
            }
        }
        res
    }
}

3159. 查询数组中元素的出现位置

给你一个整数数组 nums ，一个整数数组 queries 和一个整数 x 。

对于每个查询 queries[i] ，你需要找到 nums 中第 queries[i] 个 x 的位置，并返回它的下标。如果数组中 x 的出现次数少于 queries[i] ，该查询的答案为 -1 。

请你返回一个整数数组 answer ，包含所有查询的答案。

示例 1：

输入：nums = [1,3,1,7], queries = [1,3,2,4], x = 1

输出：[0,-1,2,-1]

解释：

第 1 个查询，第一个 1 出现在下标 0 处。
第 2 个查询，nums 中只有两个 1 ，所以答案为 -1 。
第 3 个查询，第二个 1 出现在下标 2 处。
第 4 个查询，nums 中只有两个 1 ，所以答案为 -1 。

示例 2：

输入：nums = [1,2,3], queries = [10], x = 5

输出：[-1]

解释：

第 1 个查询，nums 中没有 5 ，所以答案为 -1 。

提示：

1 <= nums.length, queries.length <= 105
1 <= queries[i] <= 105
1 <= nums[i], x <= 104

地址

https://leetcode.cn/contest/biweekly-contest-131/problems/find-occurrences-of-an-element-in-an-array/

题意

哈希统计

思路

统计数组中元素为 $x$ 的索引，然后统计即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。
空间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。

代码

impl Solution {
    pub fn occurrences_of_element(nums: Vec<i32>, queries: Vec<i32>, x: i32) -> Vec<i32> {
        let mut cnt = Vec::new();
        for i in 0..nums.len() {
            if nums[i] == x {
                cnt.push(i as i32);
            }
        }
        
        let mut res = Vec::new();
        for &q in queries.iter() {
            if q <= cnt.len() as i32 {
                res.push(cnt[q as usize - 1]);
            } else {
                res.push(-1);
            }
        }
        res
    }
}

class Solution:
    def occurrencesOfElement(self, nums: List[int], queries: List[int], x: int) -> List[int]:
        cnt = [i for i in range(len(nums)) if nums[i] == x]
        return [cnt[q - 1] if q <= len(cnt) else -1 for q in queries]

3160. 所有球里面不同颜色的数目

给你一个整数 limit 和一个大小为 n x 2 的二维数组 queries 。

总共有 limit + 1 个球，每个球的编号为 [0, limit] 中一个 互不相同 的数字。一开始，所有球都没有颜色。queries 中每次操作的格式为 [x, y] ，你需要将球 x 染上颜色 y 。每次操作之后，你需要求出所有球中不同颜色的数目。

请你返回一个长度为 n 的数组 result ，其中 result[i] 是第 i 次操作以后不同颜色的数目。

注意，没有染色的球不算作一种颜色。

示例 1：

输入：limit = 4, queries = [[1,4],[2,5],[1,3],[3,4]]

输出：[1,2,2,3]

解释：

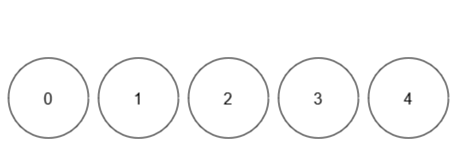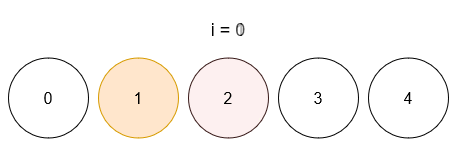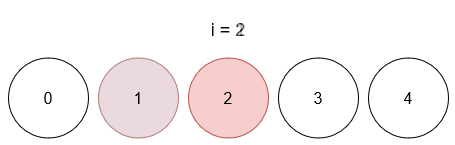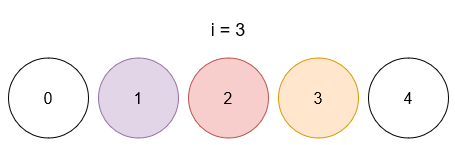
操作 0 后，球 1 颜色为 4 。
操作 1 后，球 1 颜色为 4 ，球 2 颜色为 5 。
操作 2 后，球 1 颜色为 3 ，球 2 颜色为 5 。
操作 3 后，球 1 颜色为 3 ，球 2 颜色为 5 ，球 3 颜色为 4 。

示例 2：

输入：limit = 4, queries = [[0,1],[1,2],[2,2],[3,4],[4,5]]

输出：[1,2,2,3,4]

解释：

操作 0 后，球 0 颜色为 1 。
操作 1 后，球 0 颜色为 1 ，球 1 颜色为 2 。
操作 2 后，球 0 颜色为 1 ，球 1 和 2 颜色为 2 。
操作 3 后，球 0 颜色为 1 ，球 1 和 2 颜色为 2 ，球 3 颜色为 4 。
操作 4 后，球 0 颜色为 1 ，球 1 和 2 颜色为 2 ，球 3 颜色为 4 ，球 4 颜色为 5 。

提示：

1 <= limit <= 109
1 <= n == queries.length <= 105
queries[i].length == 2
0 <= queries[i][0] <= limit
1 <= queries[i][1] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-131/problems/find-the-number-of-distinct-colors-among-the-balls/

题意

哈希统计

思路

复杂度：

时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度；
空间复杂度：$O(n)$；

代码

class Solution:
    def queryResults(self, limit: int, queries: List[List[int]]) -> List[int]:
        res = []
        color = {}
        cnt = defaultdict(int)
        for x, y in queries:
            if x in color:
                cnt[color[x]] -= 1
                if cnt[color[x]] == 0:
                    del cnt[color[x]]
            cnt[y] += 1
            color[x] = y
            res.append(len(cnt))
        return res

use std::collections::HashMap;

impl Solution {
    pub fn query_results(limit: i32, queries: Vec<Vec<i32>>) -> Vec<i32> {
        let mut res = Vec::new();
        let mut color = HashMap::new();
        let mut cnt = HashMap::new();

        for i in 0..queries.len() {
            let x = queries[i][0];
            let y = queries[i][1];
            if let Some(&old_color) = color.get(&x) {
                if let Some(old_count) = cnt.get_mut(&old_color) {
                    *old_count -= 1;
                    if *old_count == 0 {
                        cnt.remove(&old_color);
                    }
                }
            }
            *cnt.entry(y).or_insert(0) += 1;
            color.insert(x, y);
            res.push(cnt.len() as i32);
        }
        res
    }
}

3161. 物块放置查询

有一条无限长的数轴，原点在 0 处，沿着 x 轴正方向无限延伸。

给你一个二维数组 queries ，它包含两种操作：

操作类型 1 ：queries[i] = [1, x] 。在距离原点 x 处建一个障碍物。数据保证当操作执行的时候，位置 x 处没有任何障碍物。
操作类型 2 ：queries[i] = [2, x, sz] 。判断在数轴范围 [0, x] 内是否可以放置一个长度为 sz 的物块，这个物块需要完全放置在范围 [0, x] 内。如果物块与任何障碍物有重合，那么这个物块不能被放置，但物块可以与障碍物刚好接触。注意，你只是进行查询，并不是真的放置这个物块。每个查询都是相互独立的。

请你返回一个 boolean 数组results ，如果第 i 个操作类型 2 的操作你可以放置物块，那么 results[i] 为 true ，否则为 false 。

示例 1：

输入：queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]

输出：[false,true,true]

解释：

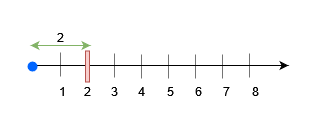
查询 0 ，在 x = 2 处放置一个障碍物。在 x = 3 之前任何大小不超过 2 的物块都可以被放置。

示例 2：

输入：queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]

输出：[true,true,false]

解释：

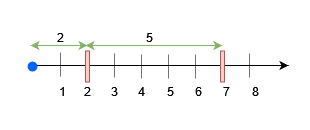
查询 0 在 x = 7 处放置一个障碍物。在 x = 7 之前任何大小不超过 7 的物块都可以被放置。
查询 2 在 x = 2 处放置一个障碍物。现在，在 x = 7 之前任何大小不超过 5 的物块可以被放置，x = 2 之前任何大小不超过 2 的物块可以被放置。

提示：

1 <= queries.length <= 15 * 104
2 <= queries[i].length <= 3
1 <= queries[i][0] <= 2
1 <= x, sz <= min(5 * 104, 3 * queries.length)
输入保证操作 1 中，x 处不会有障碍物。
输入保证至少有一个操作类型 2 。

地址

https://leetcode.cn/contest/biweekly-contest-131/problems/block-placement-queries/

题意

线段树

思路

做题的时候知道这个题目是需要用线段树，但是不知道该怎么转化这个题目，后来看了别人的解答，大概知道是怎么写该题的，然后按照别人的思路自己写了一遍，感觉没有那么难，只需要单点更新即可，不需要 $lazy$ 更新。我们用 $nums[x]$ 表示 $x$ 距离左边的最近的障碍物的距离，当然我们不需要统计所有坐标，那样需要范围更新非常麻烦，此时我们可以设:
- 如果 $x$ 处放置的不是障碍物，则此时 $nums[x] = 0$；
- 如果 $x$ 处放置的是障碍物，则此时 $nums[x] = len$, 同时 $x - len$ 处也放置的为障碍物。
- 如果当前为操作 $1$，我们利用二分查找距离 $x$ 的右侧最近的障碍物的坐标为 $right$，此时未更新的 $right$ 的左边最近的障碍物的位置为 $right - cnt[right]$，当我们在 $x$ 处放置一个障碍物时，此时 $right$ 左侧最近的障碍物的位置即为 $x$, 此时 $cnt[right] = right - x$，此时 $x$ 的左侧最近的障碍物的位置为 $right - cnt[right]$, 此时更新 $cnt[x] = cnt[right] - (right - x)$, 在线段树上同时进行两次单点更新；
- 如果当前为操作 $2$ 时，由于不一定每个位置都保存的有障碍物的信息，此时我们需要检测两个位置：
  - 此时距离 $x$ 左边最近的障碍物 $left = right - cnt[right]$, 我们检测 $x - left \ge sz$ 是否满足；
  - 同时利用线段树查找 $[0,left]$ 区间内的最大值是否满足大于等于 $sz$ ；
复杂度分析：

时间复杂度：$O(m \times \log n)$，其中 $m$ 表示给定查询的数组的长度， $n$ 表示给定的最大值；
空间复杂度：$O(n)$， $n$ 表示给定的最大值；

代码

#define CHL(x) (x * 2)
#define CHR(x) (x * 2 + 1)
const int MAXN = 4e5 + 7;

struct SegTreeNode {
    int l, r;
    int maxVal;
};

SegTreeNode tree[MAXN];

void pushUpTree(int idx) {
    tree[idx].maxVal = max(tree[CHL(idx)].maxVal, tree[CHR(idx)].maxVal);
}

void buildTree(int idx, int l, int r) {
    if (l > r) {
        return;
    }
    if (l == r) {
        tree[idx].l = tree[idx].r = l;
        tree[idx].maxVal = 0;
        return;
    }
    tree[idx].l = l;
    tree[idx].r = r;
    
    int mid = (l + r) / 2;
    buildTree(CHL(idx), l, mid);
    buildTree(CHR(idx), mid + 1, r);
    pushUpTree(idx);
}

void updateTree(int x, int val, int idx) {
    if (x < tree[idx].l || x > tree[idx].r) {
        return;
    }
    if (x == tree[idx].l && x == tree[idx].r) {
        tree[idx].maxVal = val;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) / 2;
    if (x <= mid) {
        updateTree(x, val, CHL(idx));
    } else {
        updateTree(x, val, CHR(idx));
    }
    pushUpTree(idx);
}

int queryTree(int l, int r, int idx) {
    if (r < tree[idx].l || l > tree[idx].r) {
        return 0;
    }
    if (l <= tree[idx].l && r >= tree[idx].r) {
        return tree[idx].maxVal;
    }
    int mid = (tree[idx].l + tree[idx].r) / 2;
    if (r <= mid) {
        return queryTree(l, r, CHL(idx));
    } else if (l > mid) {
        return queryTree(l, r, CHR(idx));
    } else {
        return max(queryTree(l, mid, CHL(idx)), queryTree(mid + 1, r, CHR(idx)));
    }
}

class Solution {
public:
    vector<bool> getResults(vector<vector<int>>& queries) {
        int n = queries.size();
        int m = min(50000, 3 *n);
        map<int, int> cnt;
        buildTree(1, 0, m + 1);
        
        cnt[m] = m;
        updateTree(m, m, 1);
        updateTree(0, 0, 1);
        vector<bool> res;
        for (auto &vec : queries) {
            int x = vec[1];
            auto it = cnt.lower_bound(x);
            int right = it->first, len = it->second;
            int left = right - len;
            if (vec[0] == 1) {
                updateTree(right, right - x, 1);
                updateTree(x, x - left, 1);
                cnt[right] = right - x;
                cnt[x] = x - left;
            } else {
                if (x - left >= vec[2]) {
                    res.emplace_back(true);
                } else {
                    res.emplace_back(queryTree(0, left, 1) >= vec[2]);
                }
            }
        }
        
        return res;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 哪些奋斗者

Tags: 题解力扣周赛赛

← leetcode weekly contest 399 leetcode weekly contest 400 →

扫描二维码，分享此文章