且听疯吟

leetcode biweekly contest 130

2024-05-24

leetcode biweekly contest 130

t4 又是一个难的数学题目。

3142. 判断矩阵是否满足条件

给你一个大小为 m x n 的二维矩阵 grid 。你需要判断每一个格子 grid[i][j] 是否满足：

  • 如果它下面的格子存在，那么它需要等于它下面的格子，也就是 grid[i][j] == grid[i + 1][j] 。
  • 如果它右边的格子存在，那么它需要不等于它右边的格子，也就是 grid[i][j] != grid[i][j + 1] 。

如果 所有 格子都满足以上条件，那么返回 true ，否则返回 false 。

示例 1：

输入：grid = [[1,0,2],[1,0,2]]

输出：true

解释：

img

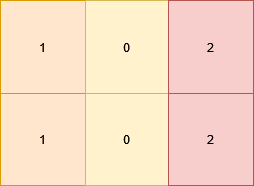
网格图中所有格子都符合条件。

示例 2：

输入：grid = [[1,1,1],[0,0,0]]

输出：false

解释：

img

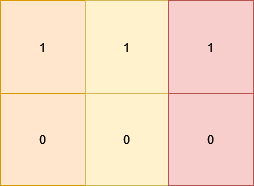
同一行中的格子值都相等。

示例 3：

输入：grid = [[1],[2],[3]]

输出：false

解释：

img

同一列中的格子值不相等。

提示：

  • 1 <= n, m <= 10
  • 0 <= grid[i][j] <= 9

地址

https://leetcode.cn/contest/biweekly-contest-130/problems/check-if-grid-satisfies-conditions/

题意

直接模拟

思路

  1. 直接模拟即可，检测每个元素是否满足题目要求即可。
  2. 复杂度分析：
  • 时间复杂度：$O(mn)$。
  • 空间复杂度：$O(1)$。

代码

class Solution:
    def satisfiesConditions(self, grid: List[List[int]]) -> bool:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i + 1 < len(grid) and grid[i][j] != grid[i + 1][j]:
                    return False
                if j + 1 < len(grid[0]) and grid[i][j] == grid[i][j + 1]:
                    return False
        return True
impl Solution {
    pub fn satisfies_conditions(grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        for i in 0..m {
            for j in 0..n {
                if i + 1 < m && grid[i][j] != grid[i + 1][j] {
                    return false;
                }
                if j + 1 < n && grid[i][j] == grid[i][j + 1] {
                    return false;
                }
            }
        }
        true
    }
}

3143. 正方形中的最多点数

给你一个二维数组 points 和一个字符串 s ，其中 points[i] 表示第 i 个点的坐标，s[i] 表示第 i 个点的 标签 。

如果一个正方形的中心在 (0, 0) ，所有边都平行于坐标轴，且正方形内 不 存在标签相同的两个点，那么我们称这个正方形是 合法 的。

请你返回 合法 正方形中可以包含的 最多 点数。

注意：

  • 如果一个点位于正方形的边上或者在边以内，则认为该点位于正方形内。
  • 正方形的边长可以为零。

示例 1：

img

输入：points = [[2,2],[-1,-2],[-4,4],[-3,1],[3,-3]], s = “abdca”

输出：2

解释：

边长为 4 的正方形包含两个点 points[0] 和 points[1] 。

示例 2：

img

输入：points = [[1,1],[-2,-2],[-2,2]], s = “abb”

输出：1

解释：

边长为 2 的正方形包含 1 个点 points[0] 。

示例 3：

输入：points = [[1,1],[-1,-1],[2,-2]], s = “ccd”

输出：0

解释：

任何正方形都无法只包含 points[0] 和 points[1] 中的一个点，所以合法正方形中都不包含任何点。

提示：

  • 1 <= s.length, points.length <= 105
  • points[i].length == 2
  • -109 <= points[i][0], points[i][1] <= 109
  • s.length == points.length
  • points 中的点坐标互不相同。
  • s 只包含小写英文字母。

地址

https://leetcode.cn/contest/biweekly-contest-130/problems/maximum-points-inside-the-square/

题意

贪心，二分查找

思路

  1. 我们知道对于一个点 $(x, y)$ 处于边长为 $2l$ 的正方形中，此时需要满足 $\max(|x|, |y|) \le l$，此时我们按照所有点的坐标的最大值进行排序，每次计算在给定的范围内，计算当前范围构成的正方形是否存在两个标签相同的点即可。当然另一种方法是二分查找，思路比较简单，在此不再描述。
  2. 复杂度分析：
  • 时间复杂度：$O(n \log n)$，其中 $n$ 表示给定的数组的长度。
  • 空间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。

代码

class Solution:
    def maxPointsInsideSquare(self, points: List[List[int]], s: str) -> int:
        arr = []
        for i in range(len(points)):
            arr.append((max(abs(points[i][0]), abs(points[i][1])), s[i]))
        arr.sort()
        
        flag = [False] * 26
        w = 0
        for i in range(min(len(points), 26)):
            if flag[ord(arr[i][1]) - ord('a')] is True:
                return i
            flag[ord(arr[i][1]) - ord('a')] = True
        return 0

3144. 分割字符频率相等的最少子字符串

给你一个字符串 s ，你需要将它分割成一个或者更多的 平衡 子字符串。比方说，s == "ababcc" 那么 ("abab", "c", "c") ，("ab", "abc", "c") 和 ("ababcc") 都是合法分割，但是 ("a", **"bab"**, "cc") ，(**"aba"**, "bc", "c") 和 ("ab", **"abcc"**) 不是，不平衡的子字符串用粗体表示。

请你返回 s 最少 能分割成多少个平衡子字符串。

注意：一个 平衡 字符串指的是字符串中所有字符出现的次数都相同。

示例 1：

输入：s = “fabccddg”

输出：3

解释：

我们可以将 s 分割成 3 个子字符串：("fab, "ccdd", "g") 或者 ("fabc", "cd", "dg") 。

示例 2：

输入：s = “abababaccddb”

输出：2

解释：

我们可以将 s 分割成 2 个子字符串：("abab", "abaccddb") 。

提示：

  • 1 <= s.length <= 1000
  • s 只包含小写英文字母。

地址

https://leetcode.cn/contest/biweekly-contest-130/problems/minimum-substring-partition-of-equal-character-frequency/

题意

滑动窗口

思路

  1. 题目本身不是太难，主要是如果暴力统计的话 $26n^2$ 的复杂度会超时，此时需要进一步优化，我们直接统计区间 $[i,j]$ 中每个字符出现的频次，每次 $j$ 移动时，同时更新字符 $s[j]$ 的频次，检测如果区间内只存在一个频次的即为合法的分割 。 稍微需要一点技巧，我们用一个哈希表 $freq$ 统计频次出现的次数，实时动态更新，当 $freq$ 中只有一个频次时，则该分割为合法分割。

  2. 复杂度：

  • 时间复杂度：$O(n^2)$，其中 $n$ 表示给定的字符串的长度；
  • 空间复杂度：$O(n)$；

代码

class Solution:
    def minimumSubstringsInPartition(self, s: str) -> int:
        n = len(s)
        dp = [n] * n
        for i in range(n):
            cnt = [0] * 26
            freq = {}
            for j in range(i, -1, -1):
                x = cnt[ord(s[j]) - ord('a')]
                if x in freq:
                    freq[x] -= 1
                    if freq[x] == 0:
                        del freq[x]
                cnt[ord(s[j]) - ord('a')] += 1
                freq[cnt[ord(s[j]) - ord('a')]] = freq.get(cnt[ord(s[j]) - ord('a')], 0) + 1
                if len(freq) == 1:
                    if j == 0:
                        dp[i] = 1
                    else:
                        dp[i] = min(dp[i], dp[j - 1] + 1)
        return dp[n - 1]

3145. 大数组元素的乘积

一个整数 x 的 强数组 指的是满足和为 x 的二的幂的最短有序数组。比方说，11 的强数组为 [1, 2, 8] 。

我们将每一个正整数 i （即1，2，3等等）的 强数组 连接得到数组 big_nums ，big_nums 开始部分为 [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, ...] 。

给你一个二维整数数组 queries ，其中 queries[i] = [fromi, toi, modi] ，你需要计算 (big_nums[fromi] * big_nums[fromi + 1] * ... * big_nums[toi]) % modi 。

请你返回一个整数数组 answer ，其中 answer[i] 是第 i 个查询的答案。

示例 1：

输入：queries = [[1,3,7]]

输出：[4]

解释：

只有一个查询。

big_nums[1..3] = [2,1,2] 。它们的乘积为 4 ，4 对 7 取余数得到 4 。

示例 2：

输入：queries = [[2,5,3],[7,7,4]]

输出：[2,2]

解释：

有两个查询。

第一个查询：big_nums[2..5] = [1,2,4,1] 。它们的乘积为 8 ，8 对 3 取余数得到 2 。

第二个查询：big_nums[7] = 2 ，2 对 4 取余数得到 2 。

提示：

  • 1 <= queries.length <= 500
  • queries[i].length == 3
  • 0 <= queries[i][0] <= queries[i][1] <= 1015
  • 1 <= queries[i][2] <= 105

地址

https://leetcode.cn/contest/biweekly-contest-130/problems/find-products-of-elements-of-big-array/

题意

二分查找，数学，位运算

思路

  1. 题目算是比较难的数学题目，但确实是个比较值得思考的题目。也可以说是一个数学题目，分析如下：

    我们先来计算一个问题，$[1,2^i]$ 组成的强数组中有多少个元素？所有元素组成的乘积又是 $2$ 的多少次幂数?此事直接计算似乎不太好计算，但是我们可以参考力扣中的一个题目: [1969. 数组元素的最小非零乘积] 。

    • $[1,2^i]$ 可以组成的元素本质即统计所有元素中 $1$ 的个数，通过 [1969. 数组元素的最小非零乘积] 可以知道，我们可以通过交换，可以将区间 $[1,2^i-1]$ 数在相同位上进行交换刚好可以组成 $2^{i-1}$ 个 $2^{i}-1$，即 $sum_{j=1}^{2^i - 1} = 2^{i-1} \times (2^i-1)$，此时再加上 $2^i$ ，由于每个 $2^{i} - 1$ 可以拆分为 $i$ 个 $2$ 的幂数，此时再加上 $2^i$ ，此时 $[1,2^i]$ 组成的强数组中含有的元素数目即为 $f(i) = i\times 2^{i-1} + 1$ 个；

    • $[1,2^i]$ 可以组成的元素本质即统计所有元素中 $1$ 的个数，通过 [1969. 数组元素的最小非零乘积] 可以知道，我们可以通过交换，可以将区间 $[1,2^i-1]$ 数在相同位上进行交换刚好可以组成 $2^{i-1}$ 个 $2^{i}-1$，即 $sum_{j=1}^{2^i - 1} = 2^{i-1} \times (2^i-1)$，此时再加上 $2^i$ ，由于 $2^0$ 的幂数为 $0$，此时每个 $2^{i} - 1$ 可以拆分为 $2$ 的幂数即为 $1 + 2 + 3 + \cdots + i - 2 + i - 1 = \dfrac{i \times (i - 1)}{2}$，此时再加上 $2^i$ 的幂数为 $i$，此时可以得到 $[1,2^i]$ 组程的强数组元素乘积中 $2$ 的幂数为 $g(i) = \dfrac{i \times (i - 1)}{2} + 1$​ ；

    • 我们再来观察 $[1,x]$ 组成的强数组中的元素数目，设 $f(x)$ 表示 $[1,x]$ 的元素含有的元素数目，对 $x$ 来说，假设$x = 2^{c_0} + 2^{c_1} + \cdots 2^{c_{m-1}}$, 此时所有小于等于 $2^{c_0}$ 的元素数目即为 $f(i)$, 所有大于 $2^{c_0}$ 的元素来说都含有一个元素为 $2^{c_0}$, 此时可以得到 $f(x) = f(2^{c_0}) + (x - 2^{c0}) + f(x - 2^{c_0})$, 此时我们很容易得到递推公式为:
      $$
      f(x) = f(2^{c_0}) + f(2^{c_1}) + \cdots + f(2^{c_{m-1}}) + x - 2^{c_0} + x - 2^{c_0} - 2^{c_1} \cdots + x -2^{c_0} - 2^{c_1} - \cdots 2^{c_{m-1}} \
      = \sum_{i=0}^{m-1}f(2^{c_i}) + (m - 1) \times 2^{c_{m-1}} + (m - 1) \times 2^{c_{m-2}} + \cdots + 2^{c_{1}}
      $$

      我们再来计算 $[1,x]$ 组成的强数组中乘积 $2$ 的幂数，设 $g(x)$ 表示 $[1,x]$ 的元素含有的元素数目，对 $x$ 来说，假设$x = 2^{c_0} + 2^{c_1} + \cdots 2^{c_{m-1}}$, 此时所有小于等于 $2^{c_0}$ 的元素乘积构成的幂数即为 $g(i)$, 所有大于 $2^{c_0}$ 的元素来说都含有一个元素为 $2^{c_0}$, 此时可以得到 $f(x) = f(2^{c_0}) + c_0 \times (x - 2^{c0}) + f(x - 2^{c_0})$, 此时我们很容易得到递推公式为:
      $$
      f(x) = f(2^{c_0}) + f(2^{c_1}) + \cdots + f(2^{c_{m-1}}) + c_0 \times (x - 2^{c_0}) + c_1 \times (x - 2^{c_0} - 2^{c_1}) \cdots + c_{m-1} \times (x -2^{c_0} - 2^{c_1} - \cdots 2^{c_{m-1}}) \
      $$

  2. 根据 $1$ 的分析我们再回到问题本身来看每次需要计算 $[x,y]$ 之间的乘积，此时我们需要找到 $[1,x-1]$ 之间乘积的幂数 $c_0$，然后再找到 $[1,y]$ 之间的幂数 $c_1$ ，此时 $c_1 - c_0$ 即等于 $[x,y]$ 之间的幂数，由于我们很容易可以通过二分查找找到 $x$ 个强数组元素中最大元素 $a$，此时再找到 $y$ 个强数组元素中的最大元素 $b$，由于 $x$ 个元素很有可能并不刚好满足 $[1,a]$ ，此时需要处理边界问题，将最高位的去掉即可。然后我们找到满足题目要求即可，然后计算出所有幂数, 然后用快速幂计算并取模返回即可。

  3. 复杂度分析：

  • 时间复杂度：$O(n \times \log^2 U)$，其中 $n$ 表示给定查询的数组的长度， $U$ 表示给定查询中元素的最大数目；
  • 空间复杂度：$O(1ogU)$， $U$ 表示给定查询中元素的最大数目；

代码

class Solution {
public:
    vector<int> findProductsOfElements(vector<vector<long long>>& queries) {
        vector<long long> f(64, 1);
        vector<long long> g(64, 0);
        for (int i = 1; i < 50; i++) {
            f[i] = i * (1LL << (i - 1)) + 1;
            g[i] = i * (i - 1) / 2 * (1LL << (i - 1)) + i;
        }
        
        /* 计算小于等于 x 的强数组中元素的个数 */
        auto calc = [&](long long x) -> long long {
            long long res = 0;
            for (int i = 63; i >= 0 && x > 0; i--) {
                if (x & (1LL << i)) {
                    x -= 1L << i;
                    res += f[i] + x;
                }
            }
            return res;
        };

        /* 计算小于等于 x 的强数组中元素的乘积中 2 的幂数 */
        auto get = [&](long long x) -> long long {
            long long res = 0;
            for (int i = 63; i >= 0 && x > 0; i--) {
                if (x & (1LL << i)) {
                    x -= 1L << i;
                    res += g[i] + i * x;
                }
            }
            return res;
        };

        /* 计算强数组中前 x 个元素乘积中 2 的幂数 */ 
        auto query = [&](long long x) -> long long {
            long long lo = 1, hi = x;
            long long num = 0;
            
            /* 二分查找找到 num*/
            while (lo <= hi) {
                long long mid = (lo + hi) / 2;
                if (calc(mid) >= x) {
                    num = mid;
                    hi = mid - 1;
                } else {
                    lo = mid + 1;
                }
            }
            
            /*计算从 1 到 num 中含有 2 的幂数 */
            long long res = get(num);
            /* 处理边界问题 */
            for (int i = 63, j = calc(num) - x; i >= 0 && j > 0; i--) {
                if (num & (1LL << i)) {
                    res -= i;
                    j--;
                }
            }
            return res;
        };
        
        /* 快速幂乘法 */
        auto fastpow = [](long long x, long long n, long long mod) {
            long long res = 1;
            for (; n != 0; n >>= 1) {
                if (n & 1) {
                    res = res * x % mod;
                }
                x = x * x % mod;
            }
            return res % mod;
        };
        
        vector<int> res;
        for (auto q : queries) {
            res.emplace_back(fastpow(2, query(q[1] + 1) - query(q[0]), q[2]));
        }
        return res;
    }
};

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode weekly contest 398 leetcode weekly contest 396 →

扫描二维码，分享此文章