leetcode contest 394

难得遇到一次手速场。

100294. 统计特殊字母的数量 I

给你一个字符串 word。如果 word 中同时存在某个字母的小写形式和大写形式，则称这个字母为 特殊字母 。

返回 word 中 特殊字母 的数量。

示例 1:

输入：word = “aaAbcBC”

输出：3

解释：

word 中的特殊字母是 'a'、'b' 和 'c'。

示例 2:

输入：word = “abc”

输出：0

解释：

word 中不存在大小写形式同时出现的字母。

示例 3:

输入：word = “abBCab”

输出：1

解释：

word 中唯一的特殊字母是 'b'。

提示：

1 <= word.length <= 50
word 仅由小写和大写英文字母组成。

地址

https://leetcode.cn/contest/weekly-contest-394/problems/count-the-number-of-special-characters-i/

题意

直接模拟

思路

题目比较简单，直接模拟即可，检测每个字符的大小写是否都出现在字符串中。
复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

代码

class Solution:
    def numberOfSpecialChars(self, word: str) -> int:
        v = set(word)
        ans = 0
        for x in ascii_lowercase:
            if x in v and x.upper() in v:
                ans += 1
        return ans

use std::collections::HashSet;

impl Solution {
    pub fn number_of_special_chars(word: String) -> i32 {
        let v: HashSet<char> = word.chars().collect();
        let mut ans = 0;
        for x in b'a'..=b'z' {
            let lower = x as char;
            let upper = lower.to_ascii_uppercase();
            if v.contains(&lower) && v.contains(&upper) {
                ans += 1;
            }
        }
        ans
    }
}

100291. 统计特殊字母的数量 II

给你一个字符串 word。如果 word 中同时出现某个字母 c 的小写形式和大写形式，并且每个小写形式的 c 都出现在第一个大写形式的 c 之前，则称字母 c 是一个 特殊字母 。

返回 word 中 特殊字母 的数量。

示例 1:

输入：word = “aaAbcBC”

输出：3

解释：

特殊字母是 'a'、'b' 和 'c'。

示例 2:

输入：word = “abc”

输出：0

解释：

word 中不存在特殊字母。

示例 3:

输入：word = “AbBCab”

输出：0

解释：

word 中不存在特殊字母。

提示：

1 <= word.length <= 2 * 105
word 仅由小写和大写英文字母组成。

地址

https://leetcode.cn/contest/weekly-contest-394/problems/count-the-number-of-special-characters-ii/

题意

模拟

思路

直接统计每个字符小写形式出现的最后一个位置 $lower_i$，以及大写形式出现的第一个位置 $upper_i$，是否满足 $upper_i > lower_i$ 即可，还是非常简单的模拟即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示给定字符串的长度。
空间复杂度：$O(1)$。

代码

class Solution:
    def numberOfSpecialChars(self, word: str) -> int:
        lower = [inf] * 26
        upper = [inf] * 26
        for i, c in enumerate(word):
            if c.islower():
                lower[ord(c) - ord('a')] = i
            else:
                if upper[ord(c) - ord('A')] == inf:
                    upper[ord(c) - ord('A')] = i
        
        return sum(1 for i in range(26) if upper[i] > lower[i] and upper[i] != inf)

impl Solution {
    pub fn number_of_special_chars(word: String) -> i32 {
        let mut lower: Vec<i32> = vec![-1; 26];
        let mut upper: Vec<i32> = vec![-1; 26];
        for (i, c) in word.chars().enumerate() {
            if c.is_ascii_lowercase() {
                lower[(c as u8 - 'a' as u8) as usize] = i as i32;
            } else {
                if upper[(c as u8 - 'A' as u8) as usize] == -1 {
                    upper[(c as u8 - 'A' as u8) as usize] = i as i32;
                }
            }
        }
        
        let mut res = 0;
        for i in 0..26 {
            if lower[i] >= 0 && upper[i] >= 0 && upper[i] > lower[i] {
                res += 1;
            }
        }
        res
    }
}

100290. 使矩阵满足条件的最少操作次数

给你一个大小为 m x n 的二维矩形 grid 。每次操作中，你可以将任一格子的值修改为任意非负整数。完成所有操作后，你需要确保每个格子 grid[i][j] 的值满足：

如果下面相邻格子存在的话，它们的值相等，也就是 grid[i][j] == grid[i + 1][j]（如果存在）。
如果右边相邻格子存在的话，它们的值不相等，也就是 grid[i][j] != grid[i][j + 1]（如果存在）。

请你返回需要的最少操作数目。

示例 1：

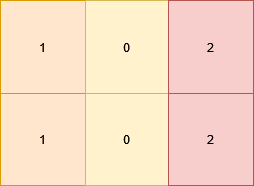
输入：grid = [[1,0,2],[1,0,2]]

输出：0

解释：

矩阵中所有格子已经满足要求。

示例 2：

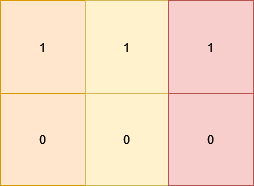
输入：grid = [[1,1,1],[0,0,0]]

输出：3

解释：

将矩阵变成 [[1,0,1],[1,0,1]] ，它满足所有要求，需要 3 次操作：

将 grid[1][0] 变为 1 。
将 grid[0][1] 变为 0 。
将 grid[1][2] 变为 1 。

示例 3：

输入：grid = [[1],[2],[3]]

输出：2

解释：

这个矩阵只有一列，我们可以通过 2 次操作将所有格子里的值变为 1 。

提示：

1 <= n, m <= 1000
0 <= grid[i][j] <= 9

地址

https://leetcode.cn/contest/weekly-contest-394/problems/minimum-number-of-operations-to-satisfy-conditions/

题意

动态规划

思路

题目给的数据量导致该题目变为简单题目了，实际应该不限定矩阵中每个元素的范围，题目才变的稍微有点难度，否则题目变的过于简单了。实际不限定元素的范围，题目的难度更合适一些，此时我们只需要统计每一列中出现频度最大的两个元素即可，每次递推时一定是在每列中最大的频数中选择一个即可。
复杂度：

时间复杂度：$O(mn + nu^2)$，其中 $m,n$ 表示给定矩阵的行数与列数；
空间复杂度：$O(n + u)$；

代码

class Solution:
    def minimumOperations(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dp = [0] * 10
        for i in range(n):
            cnt = Counter()
            for j in range(m):
                cnt[grid[j][i]] += 1
            ndp = [inf] * 10
            for j in range(10):
                for k in range(10):
                    if j == k:
                        continue
                    ndp[j] = min(ndp[j], dp[k] + m - cnt[j])
            dp = ndp
        return min(dp)

impl Solution {
    pub fn minimum_operations(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut dp = vec![0; 10];
        
        for i in 0..n {
            let mut cnt = vec![0; 10];
            for j in 0..m {
                cnt[grid[j][i] as usize] += 1;
            }
            let mut ndp = vec![m * n; 10];
            for j in 0..10 {
                for k in 0..10 {
                    if j == k {
                        continue;
                    }
                    ndp[j] = ndp[j].min(dp[k] + m - cnt[j]);
                }
            }
            dp = ndp.clone();
        }
        return (*dp.iter().min().unwrap()) as i32;
    }
}

100276. 最短路径中的边

给你一个 n 个节点的无向带权图，节点编号为 0 到 n - 1 。图中总共有 m 条边，用二维数组 edges 表示，其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。

对于节点 0 为出发点，节点 n - 1 为结束点的所有最短路，你需要返回一个长度为 m 的 boolean 数组 answer ，如果 edges[i] 至少在其中一条最短路上，那么 answer[i] 为 true ，否则 answer[i] 为 false 。

请你返回数组 answer 。

注意，图可能不连通。

示例 1：

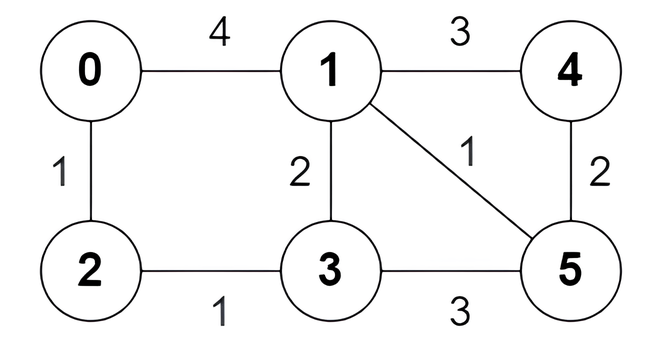
输入：n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

输出：[true,true,true,false,true,true,true,false]

解释：

以下为节点 0 出发到达节点 5 的所有最短路：

路径 0 -> 1 -> 5 ：边权和为 4 + 1 = 5 。
路径 0 -> 2 -> 3 -> 5 ：边权和为 1 + 1 + 3 = 5 。
路径 0 -> 2 -> 3 -> 1 -> 5 ：边权和为 1 + 1 + 2 + 1 = 5 。

示例 2：

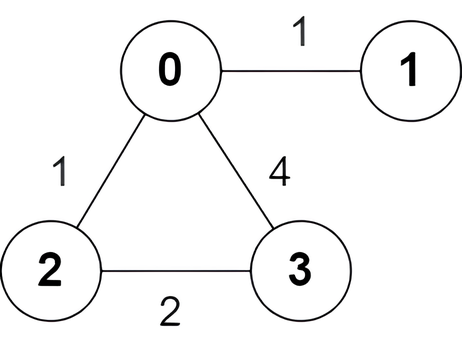
输入：n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

输出：[true,false,false,true]

解释：

只有一条从节点 0 出发到达节点 3 的最短路 0 -> 2 -> 3 ，边权和为 1 + 2 = 3 。

提示：

2 <= n <= 5 * 104
m == edges.length
1 <= m <= min(5 * 104, n * (n - 1) / 2)
0 <= ai, bi < n
ai != bi
1 <= wi <= 105
图中没有重边。

地址

https://leetcode.cn/contest/weekly-contest-394/problems/find-edges-in-shortest-paths/

题意

dijistra算法

思路

假设我们当前已经知道最短路径的长度为 $mindist$, 存在边 $e = (x,y,w)$，如果 $e$ 刚好处在在从 $0$ 到 $n-1$ 的最短路径上，假设从 $0$ 点出发到达 $x,y$ 的最短距离分别为 $dist_1[x],dist_1[y]$，从 $n-1$ 出发到达 $x,y$ 的最短距离分别为 $dist_2[x],dist_2[y]$，则此时如果 $e$ 处在最短距离的路径上。则此时一定可以得到：
$$
dist1[x] + w + dist2[y] = mindist \
dist1[y] + w + dist2[x] = mindist
$$
即最短路径可能是为 $0\rightarrow x \rightarrow y \rightarrow n-1$ 或者 $0\rightarrow y \rightarrow x \rightarrow n-1$, 此时我们检测 $e$ 是否满足关键路径要求即可。题目就变的非常模板化了，我们可以使用求单源最短路径的方法，利用 $dijstra$ 算法求出 $0,n-1$ 到所有点的最短路径，然后分别检测每条边是否满足要求即可。
复杂度分析:

时间复杂度：$O((V + E)\log V)$，其中 $V,E$ 表示节点和边的数目；
空间复杂度：$O(V + E)$，其中 $V,E$ 表示节点和边的数目；

代码

class Solution:
    def findAnswer(self, n: int, edges: List[List[int]]) -> List[bool]:
        graph = [[] for _ in range(n)]
        for x, y, cost in edges:
            graph[x].append((y, cost))
            graph[y].append((x, cost))
        
        def dijistra(start: int) -> List[int]:
            visit = [0] * n
            dist = [inf] * n
            pq = [(0, start)]
            dist[start] = 0
        
            while pq:
                (cost, x) = heapq.heappop(pq)
                if visit[x] == 1:
                    continue
                visit[x] = 1
                for nx, ncost in graph[x]:
                    if visit[nx] == 1 or cost + ncost >= dist[nx]:
                        continue
                    dist[nx] = cost + ncost
                    heapq.heappush(pq, (cost + ncost, nx))

            return dist
        
        dist1 = dijistra(0)
        dist2 = dijistra(n - 1)
        maxdist = dist1[n - 1]
        return [True if maxdist != inf and (dist1[x] + dist2[y] + cost == maxdist or dist1[y] + dist2[x] + cost == maxdist) else False for x, y, cost in edges]

use std::collections::BinaryHeap;
use std::cmp::Ordering;

impl Solution {
    pub fn find_answer(n: i32, edges: Vec<Vec<i32>>) -> Vec<bool> {
        let mut graph = vec![vec![]; n as usize];
        for i in 0..edges.len() {
            let x = edges[i][0];
            let y = edges[i][1];
            let cost = edges[i][2];
            graph[x as usize].push((y, cost));
            graph[y as usize].push((x, cost));
        }
        
        fn dijkstra(start: i32, n: usize, graph: &Vec<Vec<(i32, i32)>>) -> Vec<i64> {
            let mut dist = vec![i64::MAX; n];
            let mut visit = vec![false; n];
            let mut pq = BinaryHeap::new();

            dist[start as usize] = 0;
            pq.push((0, start));
            while let Some((cost, x)) = pq.pop() {
                if visit[x as usize] {
                    continue;
                }
                visit[x as usize] = true;
                for &(y, ncost) in &graph[x as usize] {
                    if !visit[y as usize] && dist[x as usize] + (ncost as i64) < dist[y as usize] {
                        dist[y as usize] = dist[x as usize] + ncost as i64;
                        pq.push((-dist[y as usize], y));
                    }
                }
            }
            dist
        }

   
        let dist1 = dijkstra(0, n as usize, &graph);
        let dist2 = dijkstra(n - 1, n as usize, &graph);
        let maxdist = dist1[n as usize - 1];
        let mut res = vec![false; edges.len()];
        for i in 0..edges.len() {
            let x = edges[i][0] as usize;
            let y = edges[i][1] as usize;
            let cost = edges[i][2] as i64;
            if dist1[x] != i64::MAX && dist2[y] != i64::MAX && dist1[x] + cost + dist2[y] == maxdist {
                res[i] = true;
            }
            if dist2[x] != i64::MAX && dist1[y] != i64::MAX && dist2[x] + cost + dist1[y] == maxdist {
                res[i] = true;
            }
        }
        res
    }
}

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 哪些奋斗者

Tags: 题解力扣周赛赛

← leetcode contest 393 leetcode weekly contest 395 →

扫描二维码，分享此文章