leetcode weekly contest 392

放水的一周，开心的一周周赛，手速场，感觉手速还是太慢了。

3105. 最长的严格递增或递减子数组

给你一个整数数组 nums 。

返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。

示例 1：

输入：nums = [1,4,3,3,2]

输出：2

解释：

nums 中严格递增的子数组有[1]、[2]、[3]、[3]、[4] 以及 [1,4] 。

nums 中严格递减的子数组有[1]、[2]、[3]、[3]、[4]、[3,2] 以及 [4,3] 。

因此，返回 2 。

示例 2：

输入：nums = [3,3,3,3]

输出：1

解释：

nums 中严格递增的子数组有 [3]、[3]、[3] 以及 [3] 。

nums 中严格递减的子数组有 [3]、[3]、[3] 以及 [3] 。

因此，返回 1 。

示例 3：

输入：nums = [3,2,1]

输出：3

解释：

nums 中严格递增的子数组有 [3]、[2] 以及 [1] 。

nums 中严格递减的子数组有 [3]、[2]、[1]、[3,2]、[2,1] 以及 [3,2,1] 。

因此，返回 3 。

提示：

• 1 <= nums.length <= 50
• 1 <= nums[i] <= 50

地址

https://leetcode.cn/contest/weekly-contest-392/problems/longest-strictly-increasing-or-strictly-decreasing-subarray/

题意

模拟

思路

1. 直接模拟统计所有所有递增与递减数组的长度即可。
2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def longestMonotonicSubarray(self, nums: List[int]) -> int:
        ans = 1
        maxinc, maxdec = 1, 1
        for i in range(1, len(nums)):
            if nums[i] > nums[i - 1]:
                maxinc += 1
            else:
                maxinc = 1
                
            if nums[i] < nums[i - 1]:
                maxdec += 1
            else:
                maxdec = 1
            ans = max(ans, maxinc, maxdec)
        return ans

impl Solution {
    pub fn longest_monotonic_subarray(nums: Vec<i32>) -> i32 {
        let mut ans = 1;
        let mut maxinc = 1;
        let mut maxdec = 1;
        for i in 1..nums.len() {
            if nums[i] > nums[i - 1] {
                maxinc += 1;
            } else {
                maxinc = 1;
            }
                
            if nums[i] < nums[i - 1] {
                maxdec += 1;
            } else {
                maxdec = 1;
            }
            ans = ans.max(maxinc.max(maxdec));
        }
        return ans;
    }
}

3106. 满足距离约束且字典序最小的字符串

给你一个字符串 s 和一个整数 k 。

定义函数 distance(s1, s2) ，用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离，即：

• 字符 'a' 到 'z' 按 循环 顺序排列，对于区间 [0, n - 1] 中的 i ，计算所有「 s1[i] 和 s2[i] 之间 最小距离」的 和 。

例如，distance("ab", "cd") == 4 ，且 distance("a", "z") == 1 。

你可以对字符串 s 执行 任意次 操作。在每次操作中，可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。

返回一个字符串，表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ，且满足 distance(s, t) <= k 。

示例 1：

输入：s = "zbbz", k = 3
输出："aaaz"
解释：在这个例子中，可以执行以下操作：
将 s[0] 改为 'a' ，s 变为 "abbz" 。
将 s[1] 改为 'a' ，s 变为 "aabz" 。
将 s[2] 改为 'a' ，s 变为 "aaaz" 。
"zbbz" 和 "aaaz" 之间的距离等于 k = 3 。
可以证明 "aaaz" 是在任意次操作后能够得到的字典序最小的字符串。
因此，答案是 "aaaz" 。

示例 2：

输入：s = "xaxcd", k = 4
输出："aawcd"
解释：在这个例子中，可以执行以下操作：
将 s[0] 改为 'a' ，s 变为 "aaxcd" 。
将 s[2] 改为 'w' ，s 变为 "aawcd" 。
"xaxcd" 和 "aawcd" 之间的距离等于 k = 4 。
可以证明 "aawcd" 是在任意次操作后能够得到的字典序最小的字符串。
因此，答案是 "aawcd" 。

示例 3：

输入：s = "lol", k = 0
输出："lol"
解释：在这个例子中，k = 0，更改任何字符都会使得距离大于 0 。
因此，答案是 "lol" 。

提示：

• 1 <= s.length <= 100
• 0 <= k <= 2000
• s 只包含小写英文字母。

地址

https://leetcode.cn/contest/weekly-contest-392/problems/lexicographically-smallest-string-after-operations-with-constraint/

题意

贪心

思路

1. 在替换距离有限的前提下，从左到右尽量选择最小的字符填充即可。
2. 复杂度分析：

• 时间复杂度：$O(1)$。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def getSmallestString(self, s: str, k: int) -> str:
        n = len(s)
        res = []
        for c in s:
            x = ord(c) - ord('a')
            for j in range(26):
                y = min(abs(x - j), j + 26 - x)
                if y <= k:
                    res.append(chr(ord('a') + j))
                    k -= y
                    break
        return "".join(res)

impl Solution {
    pub fn get_smallest_string(s: String, k: i32) -> String {
        let mut k = k;
        let mut res = Vec::new();
        let s_chars: Vec<char> = s.chars().collect();
        let a_ord = 'a' as i32; // ASCII 值 for 'a'

        for &c in &s_chars {
            let x = c as i32 - a_ord;
            for j in 0..26 {
                let y = (x - j as i32).abs().min(j + 26 - x);
                if y <= k {
                    res.push((a_ord + j) as u8 as char);
                    k -= y as i32;
                    break;
                }
            }
        }

        res.into_iter().collect()
    }
}

3107. 使数组中位数等于 K 的最少操作数

给你一个整数数组 nums 和一个 非负 整数 k 。一次操作中，你可以选择任一元素 加 1 或者减 1 。

请你返回将 nums 中位数 变为 k 所需要的 最少 操作次数。

一个数组的中位数指的是数组按非递减顺序排序后最中间的元素。如果数组长度为偶数，我们选择中间两个数的较大值为中位数。

示例 1：

输入：nums = [2,5,6,8,5], k = 4

输出：2

解释：我们将 nums[1] 和 nums[4] 减 1 得到 [2, 4, 6, 8, 4] 。现在数组的中位数等于 k 。

示例 2：

输入：nums = [2,5,6,8,5], k = 7

输出：3

解释：我们将 nums[1] 增加 1 两次，并且将 nums[2] 增加 1 一次，得到 [2, 7, 7, 8, 5] 。

示例 3：

输入：nums = [1,2,3,4,5,6], k = 4

输出：0

解释：数组中位数已经等于 k 了。

提示：

• 1 <= nums.length <= 2 * 105
• 1 <= nums[i] <= 109
• 1 <= k <= 109

地址

https://leetcode.cn/contest/weekly-contest-392/problems/minimum-operations-to-make-median-of-array-equal-to-k/

题意

贪心

思路

1. 最直接的思路，由于中位数为 $k$，此时所有小于中位数的元素必须要要至少减少到 $k$, 所有大于中位数的元素必须要至少增加到 $k$, 我们对数组排序后，中位数直接取 $k$ ，其余的元素依次按照要求增加或者减少即可，
2. 复杂度分析：

• 时间复杂度：$O(n \times \log n)$, $n$ 表示给定数组的长度；
• 空间复杂度：$O(1)$；

代码

class Solution:
    def minOperationsToMakeMedianK(self, nums: List[int], k: int) -> int:
        n = len(nums)
        res = 0;
        nums.sort()
        for i in range(0, n // 2):
            res += max(nums[i] - k, 0)
        res += abs(nums[n // 2] - k)
        for i in range(n // 2 + 1, n):
            res += max(k - nums[i], 0)
        return res

impl Solution {
    pub fn min_operations_to_make_median_k(nums: Vec<i32>, k: i32) -> i64 {
        let mut nums = nums;
        let n = nums.len();
        let mut res = 0 as i64;
        nums.sort_unstable(); 
        for i in 0..(n / 2) {
            res += (nums[i] - k).max(0) as i64;
        }
        res += (nums[n / 2] - k).abs() as i64;
        for i in (n / 2 + 1)..n {
            res += (k - nums[i]).max(0) as i64;
        }
        res
    }
}

3108. 带权图里旅途的最小代价

给你一个 n 个节点的带权无向图，节点编号为 0 到 n - 1 。

给你一个整数 n 和一个数组 edges ，其中 edges[i] = [ui, vi, wi] 表示节点 ui 和 vi 之间有一条权值为 wi 的无向边。

在图中，一趟旅途包含一系列节点和边。旅途开始和结束点都是图中的节点，且图中存在连接旅途中相邻节点的边。注意，一趟旅途可能访问同一条边或者同一个节点多次。

如果旅途开始于节点 u ，结束于节点 v ，我们定义这一趟旅途的 代价 是经过的边权按位与 AND 的结果。换句话说，如果经过的边对应的边权为 w0, w1, w2, ..., wk ，那么代价为w0 & w1 & w2 & ... & wk ，其中 & 表示按位与 AND 操作。

给你一个二维数组 query ，其中 query[i] = [si, ti] 。对于每一个查询，你需要找出从节点开始 si ，在节点 ti 处结束的旅途的最小代价。如果不存在这样的旅途，答案为 -1 。

返回数组 answer ，其中 answer[i] 表示对于查询 i 的 最小 旅途代价。

示例 1：

输入：n = 5, edges = [[0,1,7],[1,3,7],[1,2,1]], query = [[0,3],[3,4]]

输出：[1,-1]

解释：

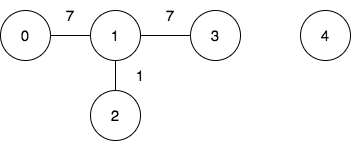
第一个查询想要得到代价为 1 的旅途，我们依次访问：0->1（边权为 7 ）1->2 （边权为 1 ）2->1（边权为 1 ）1->3 （边权为 7 ）。

第二个查询中，无法从节点 3 到节点 4 ，所以答案为 -1 。

示例 2：

输入：n = 3, edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]], query = [[1,2]]

输出：[0]

解释：

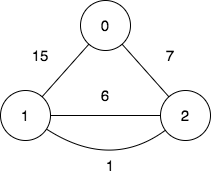
第一个查询想要得到代价为 0 的旅途，我们依次访问：1->2（边权为 1 ），2->1（边权 为 6 ），1->2（边权为 1 ）。

提示：

• 1 <= n <= 105
• 0 <= edges.length <= 105
• edges[i].length == 3
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= wi <= 105
• 1 <= query.length <= 105
• query[i].length == 2
• 0 <= si, ti <= n - 1

地址

https://leetcode.cn/contest/weekly-contest-392/problems/minimum-cost-walk-in-weighted-graph/

题意

贪心 + 计算图的连通分量，BFS， 集合

思路

1. 先看一个数学结论 $x \and y \le y$，假设这就意味着对于任意一个连通分量来说，属于连通分量的任意两点之间的最小代价即为所有边进行与的结果，本题则转变为了求图中的连通分量。求图中的连通分量则有常见的几种解法，比如 $BFS,DFS,UnionFind$ 等，题目就变的非常简单了。求出每个连通分量中的所有边，并进行与即可。
2. 复杂度分析：

• 时间复杂度：$O(n+m)$，其中 $n$ 表示给定的节点的数目， $m$ 表示给定边的数目。
• 空间复杂度：$O(n)$，其中 $n$ 表示给定边的数目

代码

class UnionFind:
    def __init__(self, weight):
        n = len(weight)
        self.parent = [0] * n
        self.rank = [0] * n
        self.cost = weight
        self.sz = [1] * n
        for i in range(n):
            self.parent[i] = i
    
    def uni(self, x: int, y: int, weight: int):
        rootx = self.find(x)
        rooty = self.find(y)
        if  rootx != rooty:
            if self.rank[rootx] > self.rank[rooty]:
                self.parent[rooty] = rootx
                self.sz[rootx] += self.sz[rooty]
            elif self.rank[rootx] < self.rank[rooty]:
                self.parent[rootx] = rooty
                self.sz[rooty] += self.sz[rootx]
            else:
                self.parent[rooty] = rootx
                self.rank[rootx] += 1
                self.sz[rootx] += self.sz[rooty]
        self.cost[rootx] = self.cost[rootx] & self.cost[rooty] & weight
        self.cost[rooty] = self.cost[rootx]
    
    def find(self, x: int) -> int:
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def size(self, x: int) -> int:
        return self.sz[self.find(x)]
    
    def weight(self, x: int) -> int:
        return self.cost[self.find(x)]
    
    def connect(self, x: int, y: int) -> bool:
        return self.find(x) == self.find(y)

class Solution:
    def minimumCost(self, n: int, edges: List[List[int]], query: List[List[int]]) -> List[int]:
        weight = [0] * n
        for x, y, cost in edges:
            weight[x] = cost
            weight[y] = cost
        
        uf = UnionFind(weight)
        for x, y, cost in edges:
            uf.uni(x, y, cost)
            
        ans = []
        for x, y in query:
            if uf.connect(x, y):
                ans.append(uf.weight(x))
            else:
                ans.append(-1)
        return ans

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu