leetcode contest 128

双周赛防水的一次，周赛难度超大的一次。

100270. 字符串的分数

给你一个字符串 s 。一个字符串的 分数 定义为相邻字符 ASCII 码差值绝对值的和。

请你返回 s 的 分数 。

示例 1：

输入：s = “hello”

输出：13

解释：

s 中字符的 ASCII 码分别为：'h' = 104 ，'e' = 101 ，'l' = 108 ，'o' = 111 。所以 s 的分数为 |104 - 101| + |101 - 108| + |108 - 108| + |108 - 111| = 3 + 7 + 0 + 3 = 13 。

示例 2：

输入：s = “zaz”

输出：50

解释：

s 中字符的 ASCII 码分别为：'z' = 122 ，'a' = 97 。所以 s 的分数为 |122 - 97| + |97 - 122| = 25 + 25 = 50 。

提示：

• 2 <= s.length <= 100
• s 只包含小写英文字母。

地址

https://leetcode.cn/contest/biweekly-contest-128/problems/score-of-a-string/

题意

直接模拟

思路

1. 直接相邻数字的差的和即可，返回即可。
2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定字符串的长度。
• 空间复杂度：$O(1)$,。

代码

class Solution:
    def scoreOfString(self, s: str) -> int:
        return sum(abs(ord(s[i]) - ord(s[i - 1])) for i in range(1, len(s)))

impl Solution {
    pub fn score_of_string(s: String) -> i32 {
        s.chars()
        .skip(1)
        .enumerate()
        .map(|(i, c)| (c as i32 - s.chars().nth(i).unwrap() as i32).abs())
        .sum()
    }
}

100280. 覆盖所有点的最少矩形数目

给你一个二维整数数组 point ，其中 points[i] = [xi, yi] 表示二维平面内的一个点。同时给你一个整数 w 。你需要用矩形 覆盖所有 点。

每个矩形的左下角在某个点 (x1, 0) 处，且右上角在某个点 (x2, y2) 处，其中 x1 <= x2 且 y2 >= 0 ，同时对于每个矩形都 必须 满足 x2 - x1 <= w 。

如果一个点在矩形内或者在边上，我们说这个点被矩形覆盖了。

请你在确保每个点都 至少 被一个矩形覆盖的前提下，最少 需要多少个矩形。

注意：一个点可以被多个矩形覆盖。

示例 1：

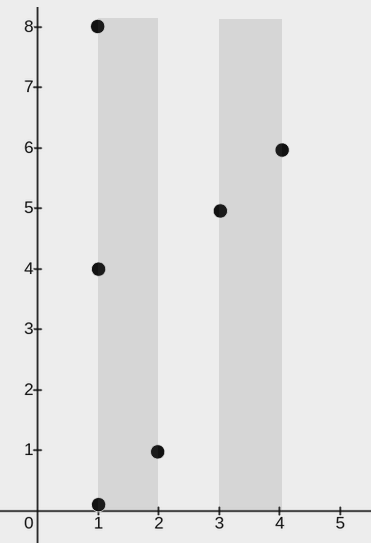
输入：points = [[2,1],[1,0],[1,4],[1,8],[3,5],[4,6]], w = 1

输出：2

解释：

上图展示了一种可行的矩形放置方案：

• 一个矩形的左下角在 (1, 0) ，右上角在 (2, 8) 。
• 一个矩形的左下角在 (3, 0) ，右上角在 (4, 8) 。

示例 2：

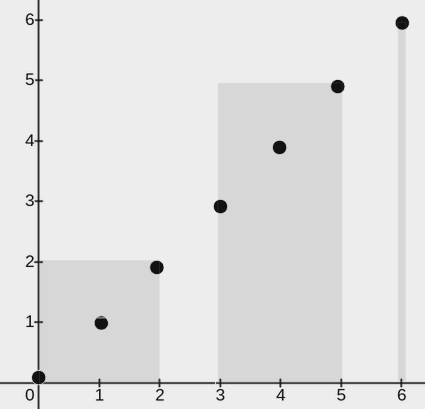
输入：points = [[0,0],[1,1],[2,2],[3,3],[4,4],[5,5],[6,6]], w = 2

输出：3

解释：

上图展示了一种可行的矩形放置方案：

• 一个矩形的左下角在 (0, 0) ，右上角在 (2, 2) 。
• 一个矩形的左下角在 (3, 0) ，右上角在 (5, 5) 。
• 一个矩形的左下角在 (6, 0) ，右上角在 (6, 6) 。

示例 3：

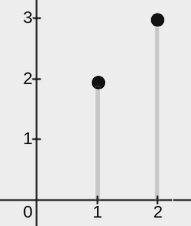
输入：points = [[2,3],[1,2]], w = 0

输出：2

解释：

上图展示了一种可行的矩形放置方案：

• 一个矩形的左下角在 (1, 0) ，右上角在 (1, 2) 。
• 一个矩形的左下角在 (2, 0) ，右上角在 (2, 3) 。

提示：

• 1 <= points.length <= 105
• points[i].length == 2
• 0 <= xi == points[i][0] <= 109
• 0 <= yi == points[i][1] <= 109
• 0 <= w <= 109
• 所有点坐标 (xi, yi) 互不相同。

地址

https://leetcode.cn/contest/biweekly-contest-128/problems/minimum-rectangles-to-cover-points/

题意

排序

思路

1. 不晓得这个题目出的有什么意思，我们每次尝试用一个 $[x, x+w]$ 的窗口去覆盖当前的坐标区域，如果当前坐标 $i$ 无法被覆盖，此时我们再增加一个新的矩形 $[x_i,x_i+w]$ 来进行覆盖，统计需要增加的矩形数目即可。
2. 复杂度分析：

• 时间复杂度：$O(n \times \log n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def minRectanglesToCoverPoints(self, points: List[List[int]], w: int) -> int:
        points.sort()
        res = 1
        end = points[0][0] + w
        for x, y in points:
            if x > end:
                end = x + w
                res += 1
        return res

impl Solution {
    pub fn min_rectangles_to_cover_points(points: Vec<Vec<i32>>, w: i32) -> i32 {
        let mut points = points;
        points.sort();
        let mut res = 1;
        let mut end = points[0][0] + w;
        for point in points {
            let x = point[0];
            if x > end {
                end = x + w;
                res += 1;
            }
        }
        res
    }
}

3112. 访问消失节点的最少时间

给你一个二维数组 edges 表示一个 n 个点的无向图，其中 edges[i] = [ui, vi, lengthi] 表示节点 ui 和节点 vi 之间有一条需要 lengthi 单位时间通过的无向边。

同时给你一个数组 disappear ，其中 disappear[i] 表示节点 i 从图中消失的时间点，在那一刻及以后，你无法再访问这个节点。

注意，图有可能一开始是不连通的，两个节点之间也可能有多条边。

请你返回数组 answer ，answer[i] 表示从节点 0 到节点 i 需要的 最少 单位时间。如果从节点 0 出发 无法 到达节点 i ，那么 answer[i] 为 -1 。

示例 1：

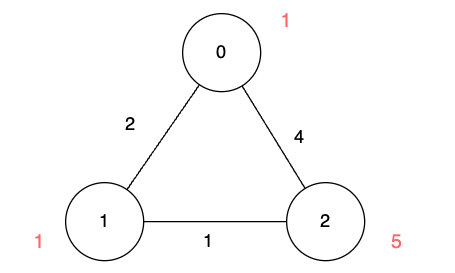
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]

输出：[0,-1,4]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

• 对于节点 0 ，我们不需要任何时间，因为它就是我们的起点。
• 对于节点 1 ，我们需要至少 2 单位时间，通过 edges[0] 到达。但当我们到达的时候，它已经消失了，所以我们无法到达它。
• 对于节点 2 ，我们需要至少 4 单位时间，通过 edges[2] 到达。

示例 2：

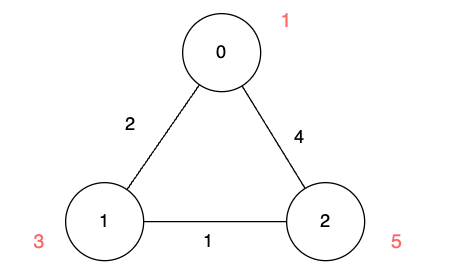
输入：n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]

输出：[0,2,3]

解释：

我们从节点 0 出发，目的是用最少的时间在其他节点消失之前到达它们。

• 对于节点 0 ，我们不需要任何时间，因为它就是我们的起点。
• 对于节点 1 ，我们需要至少 2 单位时间，通过 edges[0] 到达。
• 对于节点 2 ，我们需要至少 3 单位时间，通过 edges[0] 和 edges[1] 到达。

示例 3：

输入：n = 2, edges = [[0,1,1]], disappear = [1,1]

输出：[0,-1]

解释：

当我们到达节点 1 的时候，它恰好消失，所以我们无法到达节点 1 。

提示：

• 1 <= n <= 5 * 104
• 0 <= edges.length <= 105
• edges[i] == [ui, vi, lengthi]
• 0 <= ui, vi <= n - 1
• 1 <= lengthi <= 105
• disappear.length == n
• 1 <= disappear[i] <= 105

地址

https://leetcode.cn/contest/weekly-contest-391/problems/count-alternating-subarrays/

题意

dijistra

思路

1. 典型的 dijistra 求最短距离的模版题目，感觉没有什么好说的，照着写即可；

2. 复杂度：

• 时间复杂度：$O(n \log n)$，其中 $n$ 表示给定数组的长度；
• 空间复杂度：$O(1)$；

代码

class Solution {
public:
    vector<int> minimumTime(int n, vector<vector<int>>& edges, vector<int>& disappear) {
        vector<int> dist(n, INT_MAX);
        vector<unordered_map<int, int>> graph(n);
        vector<bool> vis(n, false);
        
        for (auto e : edges) {
            int x = e[0], y = e[1], cost = e[2];
            if (graph[x].count(y)) {
                graph[x][y] = min(graph[x][y], cost);
                graph[y][x] = min(graph[x][y], cost);
            } else {
                graph[x][y] = cost;
                graph[y][x] = cost;
            }
        }
        
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.emplace(0, 0);
        dist[0] = 0;
        
        while (!pq.empty()) {
            auto [cost, cx] = pq.top();
            pq.pop();
            if (vis[cx]) continue;
            vis[cx] = true;
            
            for (auto [nx, ncost]: graph[cx]) {
                if (cost + ncost >= disappear[nx]) continue;
                if (cost + ncost >= dist[nx]) continue;
                pq.emplace(cost + ncost, nx);
                dist[nx] = cost + ncost;
            }
        }
        
        for (int i = 0; i < n; i++) {
            if (dist[i] == INT_MAX) {
                dist[i] = -1;
            }
        }
        
        return dist;
    }
};

from collections import defaultdict
import heapq

class Solution:
    def minimumTime(self, n: int, edges: List[List[int]], disappear: List[int]) -> List[int]:
        dist = [float('inf')] * n
        graph = defaultdict(dict)
        vis = [False] * n

        for x, y, cost in edges:
            if y in graph[x]:
                graph[x][y] = min(graph[x][y], cost)
                graph[y][x] = min(graph[x][y], cost)
            else:
                graph[x][y] = cost
                graph[y][x] = cost

        pq = [(0, 0)]
        dist[0] = 0

        while pq:
            cost, cx = heapq.heappop(pq)
            if vis[cx]:
                continue
            vis[cx] = True

            for nx, ncost in graph[cx].items():
                if cost + ncost >= disappear[nx]:
                    continue
                if cost + ncost >= dist[nx]:
                    continue
                heapq.heappush(pq, (cost + ncost, nx))
                dist[nx] = cost + ncost

        for i in range(n):
            if dist[i] == float('inf'):
                dist[i] = -1

        return dist

100273. 边界元素是最大值的子数组数目

给你一个 正 整数数组 nums 。

请你求出 nums 中有多少个子数组，满足子数组中 第一个 和 最后一个 元素都是这个子数组中的 最大 值。

示例 1：

输入：nums = [1,4,3,3,2]

输出：6

解释：

总共有 6 个子数组满足第一个元素和最后一个元素都是子数组中的最大值：

• 子数组 [***1***,4,3,3,2] ，最大元素为 1 ，第一个和最后一个元素都是 1 。
• 子数组 [1,***4***,3,3,2] ，最大元素为 4 ，第一个和最后一个元素都是 4 。
• 子数组 [1,4,***3***,3,2] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [1,4,3,***3***,2] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [1,4,3,3,***2***] ，最大元素为 2 ，第一个和最后一个元素都是 2 。
• 子数组 [1,4,***3,3***,2] ，最大元素为 3 ，第一个和最后一个元素都是 3 。

所以我们返回 6 。

示例 2：

输入：nums = [3,3,3]

输出：6

解释：

总共有 6 个子数组满足第一个元素和最后一个元素都是子数组中的最大值：

• 子数组 [***3***,3,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,***3***,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,3,***3***] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [***3,3***,3] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [3,***3,3***] ，最大元素为 3 ，第一个和最后一个元素都是 3 。
• 子数组 [***3,3,3***] ，最大元素为 3 ，第一个和最后一个元素都是 3 。

所以我们返回 6 。

示例 3：

输入：nums = [1]

输出：1

解释：

nums 中只有一个子数组 [***1***] ，最大元素为 1 ，第一个和最后一个元素都是 1 。

所以我们返回 1 。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-128/

题意

单调栈

思路

1. 题目确实比较模版，对于每个 $nums[i]$$ 我们只需要找到其坐标第一个大于等于 $ $nums[i]$ 的值 $nums[j]$，此时：

   • $nums[j] = nums[i]$，此时以 $nums[i]$ 为结尾的子数组的数目即等于以 $nums[j]$ 为结尾的子数组的数目加 $1$；
   • $nums[j] > nums[i]$，此时以 $nums[i]$ 为结尾的子数组的数目即等于 $1$​；

   使用单调栈检测左侧第一个大于等于 $nums[i]$ 的值 $nums[j]$ 是否等于 $nums[i]$ 即可，当然我们还可以排序，按照从大到小的顺序来依次遍历数组，此时 $nums[i] = nums[j]$，我们可以利用二分查找检测 $[i,j]$ 中是否含有大于 $nums[i]$ 的元素即可。

2. 复杂度分析:

• 时间复杂度：$O(n)$，其中 $n$ 表示数组的长度;
• 空间复杂度：$O(n)$，其中 $n$ 表示数组的长度;

代码

class Solution:
    def numberOfSubarrays(self, nums: List[int]) -> int:
        n = len(nums)
        res = 0
        cnt = [1] * n
        stack = []
        for i, x in enumerate(nums):
            while stack and nums[stack[-1]] < x:
                stack.pop()
            if stack and nums[stack[-1]] == x:
                cnt[i] += cnt[stack[-1]]
            stack.append(i)
            res += cnt[i]
        
        return res

impl Solution {
    pub fn number_of_subarrays(nums: Vec<i32>) -> i64 {
        let n = nums.len();
        let mut res = 0;
        let mut cnt = vec![1; n];
        let mut stack: Vec<usize> = Vec::new();

        for (i, &x) in nums.iter().enumerate() {
            while let Some(&top) = stack.last() {
                if nums[top] < x {
                    stack.pop();
                } else {
                    break;
                }
            }

            if let Some(&top) = stack.last() {
                if nums[top] == x {
                    cnt[i] += cnt[top];
                }
            }

            stack.push(i);
            res += cnt[i];
        }

        res
    }
}

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu

• 关注我的微信公众号: 哪些奋斗者