leetcode contest 391

虽然没参加周赛，但是 T4 确实是个模版题目，基本上知道的知识点就非常容易。

3099. 哈沙德数

如果一个整数能够被其各个数位上的数字之和整除，则称之为 哈沙德数（Harshad number）。给你一个整数 x 。如果 x 是 哈沙德数 ，则返回 x 各个数位上的数字之和，否则，返回 -1 。

示例 1：

输入： x = 18

输出： 9

解释：

x 各个数位上的数字之和为 9 。18 能被 9 整除。因此 18 是哈沙德数，答案是 9 。

示例 2：

输入： x = 23

输出： -1

解释：

x 各个数位上的数字之和为 5 。23 不能被 5 整除。因此 23 不是哈沙德数，答案是 -1 。

提示：

1 <= x <= 100

地址

https://leetcode.cn/contest/weekly-contest-391/problems/harshad-number/

题意

直接模拟

思路

直接统计数字中每一位的和，检测是否能被 $x$ 整除即可。
复杂度分析：

时间复杂度：$O(\log x)$，其中 $x$ 表给定的数。
空间复杂度：$O(1)$,。

代码

class Solution:
    def sumOfTheDigitsOfHarshadNumber(self, x: int) -> int:
        s = sum(ord(c) - ord('0') for c in str(x))
        return s if x % s == 0 else -1

impl Solution {
    pub fn sum_of_the_digits_of_harshad_number(x: i32) -> i32 {
        let mut sum = 0;
        let mut a = x;
        while a > 0 {
            sum += a % 10;
            a /= 10;
        }
        if x % sum == 0 {sum} else {-1}
    }
}

3100. 换水问题 II

给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

喝掉任意数量的满水瓶，使它们变成空水瓶。
用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。

注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你最多可以喝到多少瓶水。

示例 1：

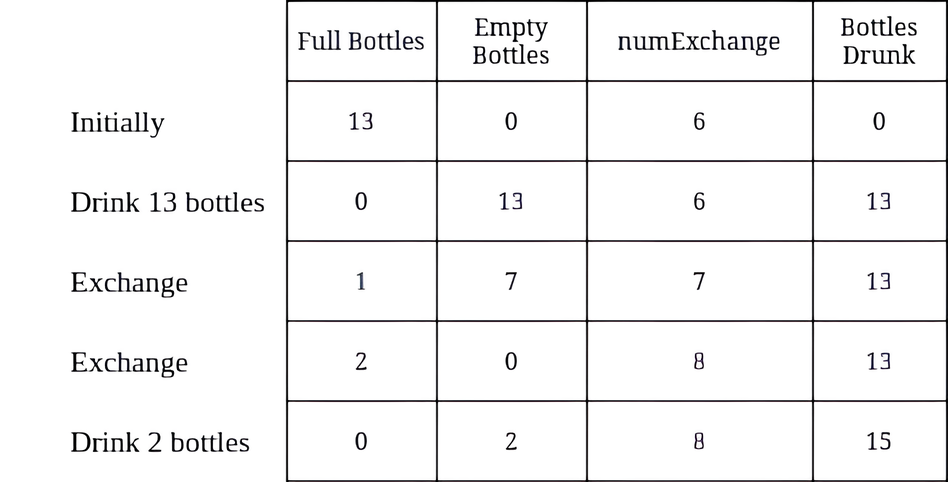
输入：numBottles = 13, numExchange = 6
输出：15
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

示例 2：

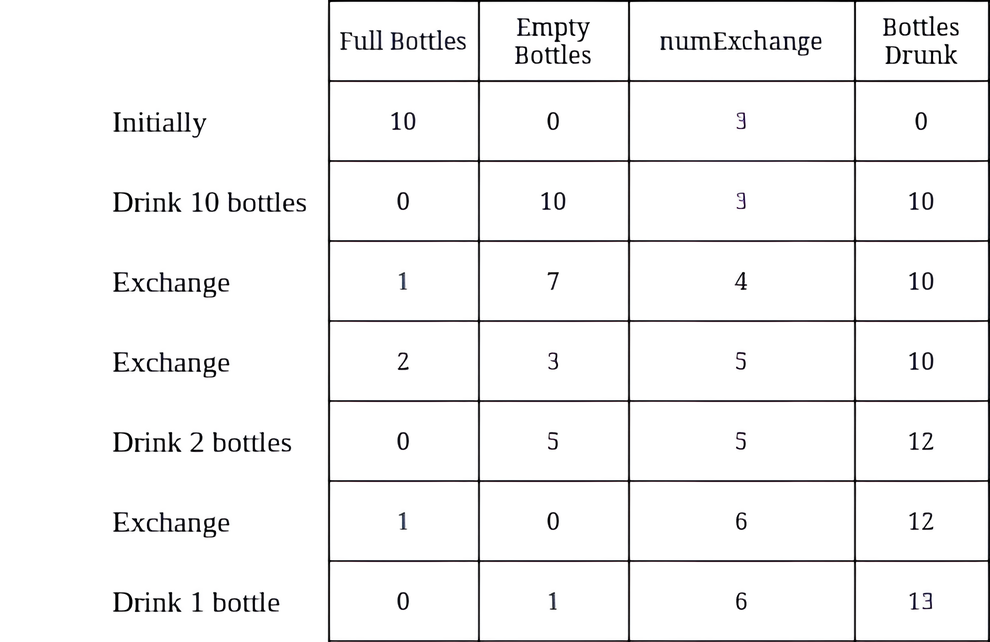
输入：numBottles = 10, numExchange = 3
输出：13
解释：上表显示了满水瓶的数量、空水瓶的数量、numExchange 的值，以及累计喝掉的水瓶数量。

提示：

1 <= numBottles <= 100
1 <= numExchange <= 100

地址

https://leetcode.cn/contest/weekly-contest-391/problems/water-bottles-ii/

题意

数学问题 + 模拟

思路

由于给定的数值较小，我们直接按照题目要求进行模拟即可。
复杂度分析：

时间复杂度：$O(n \times \log n)$，其中 $n$ 表示给定数组的长度。
空间复杂度：$O(\log n)$。

代码

impl Solution {
    pub fn max_bottles_drunk(num_bottles: i32, num_exchange: i32) -> i32 {
        let mut num_exchange = num_exchange;
        let mut res = num_bottles;
        let mut tot = num_bottles;
        while tot >= num_exchange {
            res += 1;
            tot -= num_exchange - 1;
            num_exchange += 1;
        }
        res
    }
}

class Solution:
    def maxBottlesDrunk(self, numBottles: int, numExchange: int) -> int:
        res, tot = numBottles, numBottles
        while tot >= numExchange:
            res += 1
            tot -= numExchange - 1
            numExchange += 1
        return res

3101. 交替子数组计数

给你一个二进制数组 nums 。

如果一个子数组中 不存在 两个相邻元素的值相同的情况，我们称这样的子数组为 交替子数组 。

返回数组 nums 中交替子数组的数量。

示例 1：

输入： nums = [0,1,1,1]

输出： 5

解释：

以下子数组是交替子数组：[0] 、[1] 、[1] 、[1] 以及 [0,1] 。

示例 2：

输入： nums = [1,0,1,0]

输出： 10

解释：

数组的每个子数组都是交替子数组。可以统计在内的子数组共有 10 个。

提示：

1 <= nums.length <= 105
nums[i] 不是 0 就是 1 。

地址

https://leetcode.cn/contest/weekly-contest-391/problems/count-alternating-subarrays/

题意

数学

思路

感觉是个比较容易得题目，我们每次计算以当前位置 $i$ 为结尾的且构成交替子数组的长度为 $cnt$，则此时以 $i$ 为结尾可以构成的交替子数组的数目也为 $cnt$ 个，我们依次统计当前的交替子数组即可。感觉算是个简单题目。
复杂度：

时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度；
空间复杂度：$O(1)$；

代码

class Solution:
    def countAlternatingSubarrays(self, nums: List[int]) -> int:
        n = len(nums)
        tot, res = 1, 1
        for i in range(1, len(nums)):
            tot = 1 if nums[i] == nums[i - 1] else tot + 1
            res += tot
        return res

impl Solution {
    pub fn count_alternating_subarrays(nums: Vec<i32>) -> i64 {
        let mut tot = 1;
        let mut res = 1 as i64;
        for i in 1..nums.len() {
            tot = if nums[i] == nums[i - 1] {1} else {tot + 1};
            res += tot as i64;
        }
        
        return res;
    }
}

3102. 最小化曼哈顿距离

给你一个下标从 0 开始的数组 points ，它表示二维平面上一些点的整数坐标，其中 points[i] = [xi, yi] 。

两点之间的距离定义为它们的曼哈顿距离。

请你恰好移除一个点，返回移除后任意两点之间的最大距离可能的最小值。

示例 1：

输入：points = [[3,10],[5,15],[10,2],[4,4]]
输出：12
解释：移除每个点后的最大距离如下所示：
- 移除第 0 个点后，最大距离在点 (5, 15) 和 (10, 2) 之间，为 |5 - 10| + |15 - 2| = 18 。
- 移除第 1 个点后，最大距离在点 (3, 10) 和 (10, 2) 之间，为 |3 - 10| + |10 - 2| = 15 。
- 移除第 2 个点后，最大距离在点 (5, 15) 和 (4, 4) 之间，为 |5 - 4| + |15 - 4| = 12 。
- 移除第 3 个点后，最大距离在点 (5, 15) 和 (10, 2) 之间的，为 |5 - 10| + |15 - 2| = 18 。
在恰好移除一个点后，任意两点之间的最大距离可能的最小值是 12 。

示例 2：

输入：points = [[1,1],[1,1],[1,1]]
输出：0
解释：移除任一点后，任意两点之间的最大距离都是 0 。

提示：

3 <= points.length <= 105
points[i].length == 2
1 <= points[i][0], points[i][1] <= 108

地址

https://leetcode.cn/contest/weekly-contest-391/problems/minimize-manhattan-distances/

题意

数学

思路

直接暴力计算的话，时间复杂度为 $O(n^2)$，题目的关键在于求集合中曼哈顿零距离的变形，此时我们可以根据公式可知：
$$
|x_1-x_2| + |y_1 -y_2| = \max(x_1-x_2,x_2-x_1) + \max(y_1-y_2,y_2-y1) \
=\max(x_1-x_2+y_1-y_2, x_1-x_2+y_2-y1,x_2-x_1+y_1-y_2,x_2-x_1+y_2-y_1) \
= \max((x_1+y_1)-(x_2+y_2),(x_2+y_2)-(x_1+y_1),(x_1-y_1)-(x_2-y_2),(x_2-y_2)-(x_1-y_1)) \
= \max(|(x_1+y_1)-(x_2+y_2)|, |(x_1-y_1) - (x_2-y_2)|) \
= \max(\max(x_1+y_1,x_2+y_2)-\min(x_1+y_1,x_2+y_2),\max(x_1-y_1,x_2-y_2)-\min(x_1-y_1,x_2-y_2))
$$
根据上述等式可以知道我们只需要找到 $(x_i+y_i,x_i-y_i)$ 的最大值与最小值即可求出集合中的最大的曼哈顿距离，此时题目就变的非常简单了，我们尝试去掉每个点，并在集合中去掉其相应的值，并求出最小的最大曼哈顿距离即可。实际计算过程中，我们只需要考虑去掉曼哈顿距离最大值中的两个点其中一个即可，我们分别尝试计算即可。
复杂度分析:

时间复杂度：$O(n\log n)$，其中 $n$ 表示给定的点的数目;
空间复杂度：$O(n)$，其中 $n$ 表示数组的长度;

代码

class Solution:
    def minimumDistance(self, points: List[List[int]]) -> int:
        n = len(points)
        add, sub = [], []
        for i, (x, y) in enumerate(points):
            add.append([x + y, i])
            sub.append([x - y, i])
        add.sort()
        sub.sort()
        
        x = add[-1][0] - add[0][0]
        y = sub[-1][0] - sub[0][0]
        res = inf
        i, j = 0, 0
        if x >= y:
            i, j = add[0][1], add[-1][1]
        else:
            i, j = sub[0][1], sub[-1][1]
                
        def calc(nums, i):
            if nums[0][1] == i:
                return nums[-1][0] - nums[1][0]
            elif nums[-1][1] == i:
                return nums[-2][0] - nums[0][0]
            else:
                return nums[-1][0] - nums[0][0]
        
        res = min(res, max(calc(add, i), calc(sub, i)))
        res = min(res, max(calc(add, j), calc(sub, j)))
        
        return res

use std::cmp::min;
use std::cmp::max;

impl Solution {
    pub fn minimum_distance(points: Vec<Vec<i32>>) -> i32 {
        let n = points.len();
        let mut add: Vec<[i32; 2]> = Vec::new();
        let mut sub: Vec<[i32; 2]> = Vec::new();

        for (i, point) in points.iter().enumerate() {
            let x = point[0];
            let y = point[1];
            add.push([x + y, i as i32]);
            sub.push([x - y, i as i32]);
        }

        add.sort_by(|a, b| a.cmp(b));
        sub.sort_by(|a, b| a.cmp(b));

        let x = add.last().unwrap()[0] - add.first().unwrap()[0];
        let y = sub.last().unwrap()[0] - sub.first().unwrap()[0];
        let mut res = i32::MAX;
        let (mut i, mut j) = (0, 0);

        if x >= y {
            i = add.first().unwrap()[1] as usize;
            j = add.last().unwrap()[1] as usize;
        } else {
            i = sub.first().unwrap()[1] as usize;
            j = sub.last().unwrap()[1] as usize;
        }

        fn calc(nums: &Vec<[i32; 2]>, i: usize) -> i32 {
            if nums.first().unwrap()[1] == i as i32 {
                return nums.last().unwrap()[0] - nums[1][0];
            } else if nums.last().unwrap()[1] == i as i32 {
                return nums[nums.len() - 2][0] - nums.first().unwrap()[0];
            } else {
                return nums.last().unwrap()[0] - nums.first().unwrap()[0];
            }
        }

        res = min(res, max(calc(&add, i), calc(&sub, i)));
        res = min(res, max(calc(&add, j), calc(&sub, j)));
        res
    }
}

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 哪些奋斗者

Tags: 题解力扣周赛赛

← leetcode biweekly contest 127 leetcode biweekly contest 128 →

扫描二维码，分享此文章