且听疯吟

leetcode biweekly contest 125

2024-03-11

leetcode biweekly contest 125

双周赛没有参加，不过观察了一下 ,T4 应该是比较难得题目，AK 人数在 300 以下，准备以后题解全部都用 python 和 rust 来写一遍。

3065. 超过阈值的最少操作数 I

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

一次操作中，你可以删除 nums 中的最小元素。

你需要使数组中的所有元素都大于或等于 k ，请你返回需要的 最少 操作次数。

示例 1：

输入：nums = [2,11,10,1,3], k = 10
输出：3
解释：第一次操作后，nums 变为 [2, 11, 10, 3] 。
第二次操作后，nums 变为 [11, 10, 3] 。
第三次操作后，nums 变为 [11, 10] 。
此时，数组中的所有元素都大于等于 10 ，所以我们停止操作。
使数组中所有元素都大于等于 10 需要的最少操作次数为 3 。

示例 2：

输入：nums = [1,1,2,4,9], k = 1
输出：0
解释：数组中的所有元素都大于等于 1 ，所以不需要对 nums 做任何操作。

示例 3：

输入：nums = [1,1,2,4,9], k = 9
输出：4
解释：nums 中只有一个元素大于等于 9 ，所以需要执行 4 次操作。

提示：

  • 1 <= nums.length <= 50
  • 1 <= nums[i] <= 109
  • 1 <= k <= 109
  • 输入保证至少有一个满足 nums[i] >= k 的下标 i 存在。

地址

https://leetcode.cn/contest/biweekly-contest-125/problems/minimum-operations-to-exceed-threshold-value-i/

题意

直接模拟

思路

  1. 根据题意直接模拟，将元素排序，并且将所有小于 $k$ 的元素删除掉即可，即统计数组中小于等于 $k$ 的元素数目即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n \log n)$，其中 $n$ 表示给定数组的长度。
  • 空间复杂度：$O(\log n)$。

代码

class Solution:
    def minOperations(self, nums: List[int], k: int) -> int:
        nums.sort()
        return bisect.bisect_left(nums, k)
impl Solution {
    pub fn min_operations(nums: Vec<i32>, k: i32) -> i32 {
        let mut res = 0;
        for x in nums {
            if x < k {
                res += 1;
            }
        }
        res
    }
}

3066. 超过阈值的最少操作数 II

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

一次操作中，你将执行：

  • 选择 nums 中最小的两个整数 x 和 y 。
  • 将 x 和 y 从 nums 中删除。
  • 将 min(x, y) * 2 + max(x, y) 添加到数组中的任意位置。

注意，只有当 nums 至少包含两个元素时，你才可以执行以上操作。

你需要使数组中的所有元素都大于或等于 k ，请你返回需要的 最少 操作次数。

示例 1：

输入：nums = [2,11,10,1,3], k = 10
输出：2
解释：第一次操作中，我们删除元素 1 和 2 ，然后添加 1 * 2 + 2 到 nums 中，nums 变为 [4, 11, 10, 3] 。
第二次操作中，我们删除元素 3 和 4 ，然后添加 3 * 2 + 4 到 nums 中，nums 变为 [10, 11, 10] 。
此时，数组中的所有元素都大于等于 10 ，所以我们停止操作。
使数组中所有元素都大于等于 10 需要的最少操作次数为 2 。

示例 2：

输入：nums = [1,1,2,4,9], k = 20
输出：4
解释：第一次操作后，nums 变为 [2, 4, 9, 3] 。
第二次操作后，nums 变为 [7, 4, 9] 。
第三次操作后，nums 变为 [15, 9] 。
第四次操作后，nums 变为 [33] 。
此时，数组中的所有元素都大于等于 20 ，所以我们停止操作。
使数组中所有元素都大于等于 20 需要的最少操作次数为 4 。

提示：

  • 2 <= nums.length <= 2 * 105
  • 1 <= nums[i] <= 109
  • 1 <= k <= 109
  • 输入保证答案一定存在，也就是说一定存在一个操作序列使数组中所有元素都大于等于 k 。

地址

https://leetcode.cn/contest/biweekly-contest-125/problems/minimum-operations-to-exceed-threshold-value-ii/

题意

直接模拟

思路

  1. 题目就比较简单与直接了，直接利用最小堆进行模拟即可，每次从堆中弹出最小的两个元素 $(x,y)$, 然后队列中压入元素 $\min(x, y) * 2 + max(x,y)$，直到最小的元素都大于等于 $k$ 为止。
  2. 复杂度分析：
  • 时间复杂度：$O(n \log k)$，其中 $n$ 表示给定数组的长度。
  • 空间复杂度：$O(n)$, 其中 $n$ 分别为矩形的行数与列数。

代码

import heapq

class Solution:
    def minOperations(self, nums: List[int], k: int) -> int:
        heapq.heapify(nums)
        ans = 0
        while len(nums) > 1 and nums[0] < k:
            x = heapq.heappop(nums)
            y = heapq.heappop(nums)
            heapq.heappush(nums, min(x, y) * 2 + max(x, y))
            ans += 1
        return ans
use std::collections::BinaryHeap;
use core::cmp::Reverse;

impl Solution {
    pub fn min_operations(nums: Vec<i32>, k: i32) -> i32 {
        let mut heap = BinaryHeap::new();
        for x in nums {
            heap.push(Reverse(x as i64));
        }
        let mut ans = 0;
        while heap.len() > 1 && (*heap.peek().unwrap()).0 < k as i64{
            let x = heap.pop().unwrap().0;
            let y = heap.pop().unwrap().0;
            heap.push(Reverse(std::cmp::min(x, y) * 2 + std::cmp::max(x, y)));
            ans += 1;
        }
        ans
    }
}

3067. 在带权树网络中统计可连接服务器对数目

给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [ai, bi, weighti] 表示节点 ai 和 bi 之间有一条双向边，边的权值为 weighti 。再给你一个整数 signalSpeed 。

如果两个服务器 a ，b 和 c 满足以下条件，那么我们称服务器 a 和 b 是通过服务器 c 可连接的 ：

  • a < b ，a != c 且 b != c 。
  • 从 c 到 a 的距离是可以被 signalSpeed 整除的。
  • 从 c 到 b 的距离是可以被 signalSpeed 整除的。
  • 从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的 数目 。

示例 1：

img

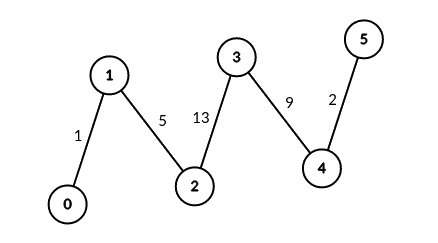
输入：edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
输出：[0,4,6,6,4,0]
解释：由于 signalSpeed 等于 1 ，count[c] 等于所有从 c 开始且没有公共边的路径对数目。
在输入图中，count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。

示例 2：

img

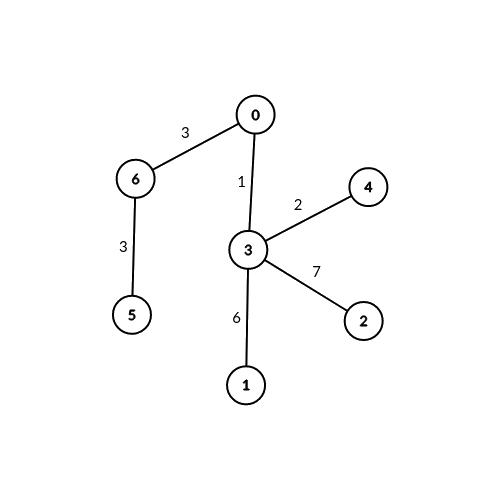
输入：edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
输出：[2,0,0,0,0,0,2]
解释：通过服务器 0 ，有 2 个可连接服务器对(4, 5) 和 (4, 6) 。
通过服务器 6 ，有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。
所有服务器对都必须通过服务器 0 或 6 才可连接，所以其他服务器对应的可连接服务器对数目都为 0 。

提示：

  • 2 <= n <= 1000
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ai, bi < n
  • edges[i] = [ai, bi, weighti]
  • 1 <= weighti <= 106
  • 1 <= signalSpeed <= 106
  • 输入保证 edges 构成一棵合法的树。

地址

https://leetcode.cn/contest/biweekly-contest-125/problems/count-pairs-of-connectable-servers-in-a-weighted-tree-network/

题意

换根 dp

思路

  1. 枚举每个节点 $C$，分别计算到点 $c$ 路径中路径和被 $signalSpeed$ 整除的数目，然后相乘即可。题目的关键在于求从 $c$ 出发构成路径和被整除的数目，此时我们可以枚举 $c$ 的子节点 $v$，每次计算从 $c\rightarrow v$ 路径中被 $s$ 整除的节点数目即可，此时用一个简单的递归实现即可。

  2. 复杂度分析：

  • 时间复杂度：$O(n^2)$, $n$ 表示给定节点的数目；
  • 空间复杂度：$O(n)$,, $n$ 表示给定节点的数目;

代码

class Solution:
    def countPairsOfConnectableServers(self, edges: List[List[int]], signalSpeed: int) -> List[int]:
        n = len(edges) + 1
        graph = [[] for _ in range(n)]
        for x, y, cost in edges:
            graph[x].append((y, cost))
            graph[y].append((x, cost))
        
        def dfs(p, root, curr) -> int:
            nonlocal signalSpeed
            res = 0
            if curr == 0: 
                res += 1
            for v, cost in graph[p]:
                if v == root:
                    continue
                res += dfs(v, p, (curr + cost) % signalSpeed)
            return res
        
        ans = [0] * n
        for i in range(n):
            now = 0
            for v, cost in graph[i]:
                cnt = dfs(v, i, cost % signalSpeed)
                ans[i] += now * cnt
                now += cnt
        return ans
impl Solution {
    pub fn count_pairs_of_connectable_servers(edges: Vec<Vec<i32>>, signal_speed: i32) -> Vec<i32> {
        let n = edges.len() + 1;
        let mut graph = vec![Vec::new(); n];
        for edge in edges.iter() {
            let x = edge[0] as usize;
            let y = edge[1] as usize;
            let cost = edge[2];
            graph[x].push((y, cost));
            graph[y].push((x, cost));
        }

        fn dfs(graph: &Vec<Vec<(usize, i32)>>, p: usize, root: usize, curr: i32, signal_speed: i32) -> i32 {
            let mut res = 0;
            if curr == 0 {
                res += 1;
            }
            for &(v, cost) in &graph[p] {
                if v == root {
                    continue;
                }
                res += dfs(graph, v, p, (curr + cost) % signal_speed, signal_speed);
            }
            res
        }
        
        let mut ans = vec![0; n];
        for i in 0..n {
            let mut now = 0;
            for &(v, cost) in &graph[i] {
                let cnt = dfs(&graph, v, i, cost % signal_speed, signal_speed);
                ans[i] += now * cnt;
                now += cnt;
            } 
        }
        ans
    }
}

3068. 最大节点价值之和

给你一棵 n 个节点的 无向 树，节点从 0 到 n - 1 编号。树以长度为 n - 1 下标从 0 开始的二维整数数组 edges 的形式给你，其中 edges[i] = [ui, vi] 表示树中节点 ui 和 vi 之间有一条边。同时给你一个 正 整数 k 和一个长度为 n 下标从 0 开始的 非负 整数数组 nums ，其中 nums[i] 表示节点 i 的 价值 。

日增哥哥想 最大化 树中所有节点价值之和。为了实现这一目标，日增哥哥可以执行以下操作 任意 次（包括 0 次）：

  • 选择连接节点 

    u

    和 

    v

    的边 

    [u, v]

    ，并将它们的值更新为：

    • nums[u] = nums[u] XOR k
    • nums[v] = nums[v] XOR k

请你返回日增哥哥通过执行以上操作 任意次 后，可以得到所有节点 价值之和 的 最大值 。

示例 1：

img

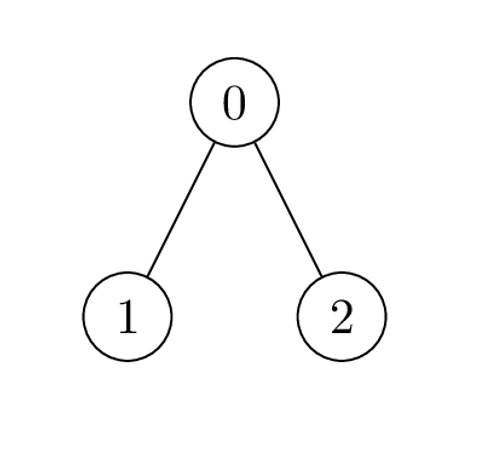
输入：nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
输出：6
解释：日增哥哥可以通过一次操作得到最大价值和 6 ：
- 选择边 [0,2] 。nums[0] 和 nums[2] 都变为：1 XOR 3 = 2 ，数组 nums 变为：[1,2,1] -> [2,2,2] 。
所有节点价值之和为 2 + 2 + 2 = 6 。
6 是可以得到最大的价值之和。

示例 2：

img

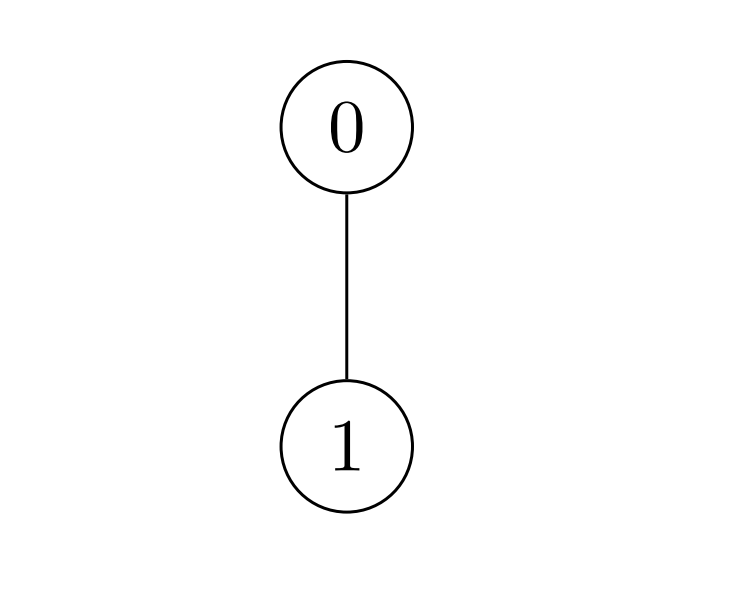
输入：nums = [2,3], k = 7, edges = [[0,1]]
输出：9
解释：日增哥哥可以通过一次操作得到最大和 9 ：
- 选择边 [0,1] 。nums[0] 变为：2 XOR 7 = 5 ，nums[1] 变为：3 XOR 7 = 4 ，数组 nums 变为：[2,3] -> [5,4] 。
所有节点价值之和为 5 + 4 = 9 。
9 是可以得到最大的价值之和。

示例 3：

img

输入：nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
输出：42
解释：日增哥哥不需要执行任何操作，就可以得到最大价值之和 42 。

提示：

  • 2 <= n == nums.length <= 2 * 104
  • 1 <= k <= 109
  • 0 <= nums[i] <= 109
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • 输入保证 edges 构成一棵合法的树。

地址

https://leetcode.cn/contest/biweekly-contest-125/problems/find-the-maximum-sum-of-node-values/

题意

贪心 + 换根dp

思路

  1. t4 确实是个非常不错的题目，难得比较好的思维题目，值得仔细思考的题目，rust 代码真是难写，编译器的各种规则确实非常蛋疼，习惯了别的语言的写法，rust 的语法确实比较怪异。首先我们需要思考一个问题，对于当前节点 $p$，
  • 如果节点 $p$ 翻转奇数次，则节点 $p$ 的值为 $k \oplus nums[p]$；
  • 如果节点 $p$ 翻转偶数次，则节点 $p$ 的值为 $nums[p]$​；

此时我们设当前每个节点在递归时返回当前节点翻转偶数次与奇数次的最大值分别为 $c_0,c_1$, 假设当前节点为 $p$，它的孩子节点分别为 $v_0, v_1,v_2, \cdots$, 假设当前遍历的孩子节点 $v$，此时 $v$ 可以选择与根节点 $p$ 翻转，也可以选择不翻转，以节点 $v$ 为根节点的子树翻转与不翻转时的最大值为 $vc_0,vc_1$,则有以下两种情况：

  • 假设当前保持不翻转，则此时当前节点 $p$ 的翻转总数此时不变，即此时的奇偶性保持不变，根据贪心原则，应当取 $vc_0, vc_1$ 二者中的最大值，但节点 $p$ 此时不进行翻转，则此时可以得到递推公式：$$c_0 = c_0 + \max(vc_0,vc_1) c_1 = c_1 + \max(vc_0,vc_1)$$;

  • 假设当前节点进行翻转，则此时当前节点 $p$ 的翻转总数 $+1$，奇偶性发生变换，此时我们应当取 $vc_0,vc_1$ 二者翻转后的最大值，则此时可以得到递推公式：$$c_0 = c_1 + \max(vc0-v + (v \oplus k), vc_1-(k \oplus v) + v), c_1 = c_0 + \max(vc0-v + (v \oplus k), vc_1-(k \oplus v) + v)$$​;

  • 综合起来上述的公式可以总结为如下：
    $$
    c_0 = \max(c_0 + \max(vc_0,vc_1), c_1 + \max(vc0-v + (v \oplus k), vc_1-(k \oplus v) + v))\
    c_1 = \max(c_1 + \max(vc_0,vc_1),c_0 + \max(vc0-v + (v \oplus k), vc_1-(k \oplus v) + v))
    $$

  • 求出所有以当前节点为根节点的子树返回不翻转与翻转时的最大值，最终返回二者的最大值即可。

  1. 仔细思考一下，实际上题目中任意两个节点都可以完成翻转，即将两个节点的值变为与 $k$ 异或后的值，并且翻转的节点数目只能为偶数，此时题目就转换为了将数组中任意偶数个元素进行翻转后可以得到的最大值，设 $c_0, c_1$ 表示翻转次数为偶数和奇数时的最大值，当前节点 $x$ 要么翻转要么保持不变，此时可以得到递推公式如下：
    $$
    c_0 = \max(c_0 + x, c_1 + x \oplus k) \
    c_1 = \max(c_1 + x, c_0 + x \oplus k)
    $$
    题目就变得非常简单，不过方法确实很难想到。

  2. 复杂度分析：

  • 时间复杂度：$O(n)$，其中 $n$ 表示给定节点的数目。
  • 空间复杂度：$O(n)$，其中 $n$ 表示给定节点的数目。

代码

class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
        n = len(nums)
        graph = [[] for _ in range(n)]
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        
        def dfs(p, root):
            # 当前偶数次翻转与奇数次翻转的最大值
            dp = [0, -inf]
            for v in graph[p]:
                if v == root:
                    continue
                c0, c1 = dfs(v, p)
                ndp = [0, 0]
                # 本次之后仍然为偶数次翻转 
                ndp[0] = max(dp[0] + max(c0, c1), dp[1] + max(c0 - nums[v] + (k ^ nums[v]), c1 - (k ^ nums[v]) + nums[v]))
                # 本次之后仍然为奇数次翻转
                ndp[1] = max(dp[1] + max(c0, c1), dp[0] + max(c0 - nums[v] + (k ^ nums[v]), c1 - (k ^ nums[v]) + nums[v]))
                dp = ndp

            return [dp[0] + nums[p], dp[1] + (k ^ nums[p])]
        
        x, y = dfs(0, -1)
        return max(x, y)
    
class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
        c0, c1 = 0, -inf
        for x in nums:
            c0, c1 = max(c0 + x, c1 + (x ^ k)), max(c1 + x, c0 + (x ^ k))
        return  c0
use std::cmp::{max, min};

impl Solution {
    pub fn maximum_value_sum(nums: Vec<i32>, k: i32, edges: Vec<Vec<i32>>) -> i64 {
        let n = nums.len();
        let mut graph = vec![Vec::new(); n];
        for edge in edges {
            let x = edge[0] as usize;
            let y = edge[1] as usize;
            graph[x].push(y);
            graph[y].push(x);
        }

        fn dfs(p: usize, root: i32, nums: &Vec<i32>, k: i32, graph: &Vec<Vec<usize>>) -> Vec<i64> {
            let mut dp = vec![0, std::i64::MIN];
            for &v in &graph[p] {
                if v as i32 == root {
                    continue;
                }
                let cnt = dfs(v, p as i32, nums, k, graph);
                let c0 = cnt[0];
                let c1 = cnt[1];
                let mut ndp = vec![0, 0];
                let val = (k ^ nums[v]) as i64;
                ndp[0] = (dp[0] + c0.max(c1)).max(dp[1] + (c0 - nums[v] as i64 + val).max(c1 - val  + nums[v] as i64));
                ndp[1] = (dp[1] + c0.max(c1)).max(dp[0] + (c0 - nums[v] as i64 + val).max(c1 - val + nums[v] as i64));
                
                dp = ndp;
            }
            vec![dp[0] + nums[p] as i64, dp[1] + (k ^ nums[p]) as i64]
        }

        let res = dfs(0, -1, &nums, k, &graph);
        return res[0].max(res[1]);
    }
}

use std::cmp::{max, min};

impl Solution {
    pub fn maximum_value_sum(nums: Vec<i32>, k: i32, edges: Vec<Vec<i32>>) -> i64 {
        let mut c0 = 0;
        let mut c1 = std::i64::MIN;

        for x in nums {
            let new_c0 = max(c0 + x as i64, c1 + (x ^ k) as i64);
            let new_c1 = max(c1 + x as i64, c0 + (x ^ k) as i64);
            c0 = new_c0;
            c1 = new_c1;
        }
        c0
    }
}

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode contest 387 leetcode contest 388 →

扫描二维码，分享此文章