leetcode contest 386

这周的 t4 难度创新高了，国服只有 25 人 AK.

100224. 分割数组

给你一个长度为偶数的整数数组 nums 。你需要将这个数组分割成 nums1 和 nums2 两部分，要求：

nums1.length == nums2.length == nums.length / 2 。
nums1 应包含 互不相同 的元素。
nums2也应包含 互不相同 的元素。

如果能够分割数组就返回 true ，否则返回 false 。

示例 1：

输入：nums = [1,1,2,2,3,4]
输出：true
解释：分割 nums 的可行方案之一是 nums1 = [1,2,3] 和 nums2 = [1,2,4] 。

示例 2：

输入：nums = [1,1,1,1]
输出：false
解释：分割 nums 的唯一可行方案是 nums1 = [1,1] 和 nums2 = [1,1] 。但 nums1 和 nums2 都不是由互不相同的元素构成。因此，返回 false 。

提示：

1 <= nums.length <= 100
nums.length % 2 == 0
1 <= nums[i] <= 100

地址

https://leetcode.cn/contest/weekly-contest-386/problems/split-the-array/

题意

直接模拟

思路

此时只需要统计数组中是否存在某个元素出现的次数大于 $2$ 即可，否则即可满足要求。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度。
空间复杂度：$O(n)$。

代码

class Solution:
    def isPossibleToSplit(self, nums: List[int]) -> bool:
        cnt = Counter(nums)
        for k, v in cnt.items():
            if v > 2:
                return False
        return True

100225. 求交集区域内的最大正方形面积

在二维平面上存在 n 个矩形。给你两个下标从 0 开始的二维整数数组 bottomLeft 和 topRight，两个数组的大小都是 n x 2 ，其中 bottomLeft[i] 和 topRight[i] 分别代表第 i 个矩形的 左下角 和 右上角 坐标。

我们定义向右的方向为 x 轴正半轴（x 坐标增加），向左的方向为 x 轴负半轴（x 坐标减少）。同样地，定义向上的方向为 y 轴正半轴（y 坐标增加），向下 的方向为 y 轴负半轴（y 坐标减少）。

你可以选择一个区域，该区域由两个矩形的交集形成。你需要找出能够放入该区域内的最大正方形面积，并选择最优解。

返回能够放入交集区域的正方形的最大可能面积，如果矩形之间不存在任何交集区域，则返回 0。

示例 1：

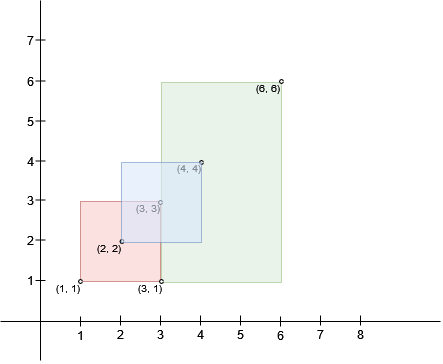
输入：bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1 的交集区域，或矩形 1 和矩形 2 的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。

示例 2：

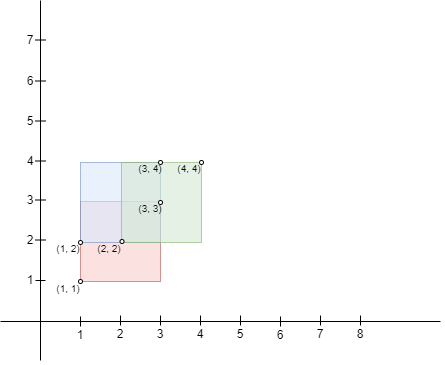
输入：bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1，矩形 1 和矩形 2，或所有三个矩形的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。
请注意，区域可以由多于两个矩形的交集构成。

示例 3：

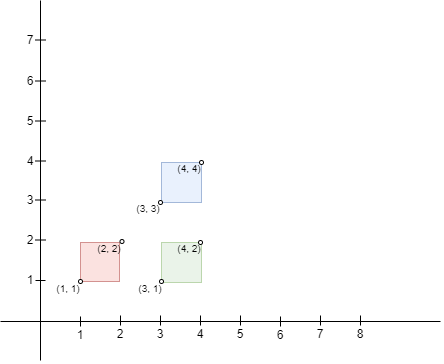
输入：bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
输出：0
解释：不存在相交的矩形，因此，返回 0 。

提示：

n == bottomLeft.length == topRight.length
2 <= n <= 103
bottomLeft[i].length == topRight[i].length == 2
1 <= bottomLeft[i][0], bottomLeft[i][1] <= 107
1 <= topRight[i][0], topRight[i][1] <= 107
bottomLeft[i][0] < topRight[i][0]
bottomLeft[i][1] < topRight[i][1]

地址

https://leetcode.cn/contest/weekly-contest-386/problems/find-the-largest-area-of-square-inside-two-rectangles/

题意

直接模拟

思路

我们计算任意两个矩形之间的交集区域，该交集区域一定为一个矩形，求出该矩形的最短边即可，该矩形的最短边即为可以构成最大正方形的边长，返回即可。
复杂度分析：

时间复杂度：$O(n^2)$，其中 $n$ 表示给定数组的长度。
空间复杂度：$O(1)$。

代码

class Solution:
    def largestSquareArea(self, bottomLeft: List[List[int]], topRight: List[List[int]]) -> int:
        def calc(a1, b1, a2, b2):
            x0, y0 = max(a1[0], a2[0]), max(a1[1], a2[1])
            x1, y1 = min(b1[0], b2[0]), min(b1[1], b2[1])
            return max(0, min(x1 - x0, y1 - y0))

        res, n = 0, len(bottomLeft)
        for i in range(n):
            for j in range(i + 1, n):
                x = calc(bottomLeft[i], topRight[i], bottomLeft[j], topRight[j])
                res = max(res, x**2)
        return res

100200. 标记所有下标的最早秒数 I

给你两个下标从 1 开始的整数数组 nums 和 changeIndices ，数组的长度分别为 n 和 m 。

一开始，nums 中所有下标都是未标记的，你的任务是标记 nums 中所有下标。

从第 1 秒到第 m 秒（包括第 m 秒），对于每一秒 s ，你可以执行以下操作之一：

选择范围 [1, n] 中的一个下标 i ，并且将 nums[i] 减少 1 。
如果 nums[changeIndices[s]] 等于 0 ，标记下标 changeIndices[s] 。
什么也不做。

请你返回范围 [1, m] 中的一个整数，表示最优操作下，标记 nums 中所有下标的 最早秒数 ，如果无法标记所有下标，返回 -1 。

示例 1：

输入：nums = [2,2,0], changeIndices = [2,2,2,2,3,2,2,1]
输出：8
解释：这个例子中，我们总共有 8 秒。按照以下操作标记所有下标：
第 1 秒：选择下标 1 ，将 nums[1] 减少 1 。nums 变为 [1,2,0] 。
第 2 秒：选择下标 1 ，将 nums[1] 减少 1 。nums 变为 [0,2,0] 。
第 3 秒：选择下标 2 ，将 nums[2] 减少 1 。nums 变为 [0,1,0] 。
第 4 秒：选择下标 2 ，将 nums[2] 减少 1 。nums 变为 [0,0,0] 。
第 5 秒，标记 changeIndices[5] ，也就是标记下标 3 ，因为 nums[3] 等于 0 。
第 6 秒，标记 changeIndices[6] ，也就是标记下标 2 ，因为 nums[2] 等于 0 。
第 7 秒，什么也不做。
第 8 秒，标记 changeIndices[8] ，也就是标记下标 1 ，因为 nums[1] 等于 0 。
现在所有下标已被标记。
最早可以在第 8 秒标记所有下标。
所以答案是 8 。

示例 2：

输入：nums = [1,3], changeIndices = [1,1,1,2,1,1,1]
输出：6
解释：这个例子中，我们总共有 7 秒。按照以下操作标记所有下标：
第 1 秒：选择下标 2 ，将 nums[2] 减少 1 。nums 变为 [1,2] 。
第 2 秒：选择下标 2 ，将 nums[2] 减少 1 。nums 变为 [1,1] 。
第 3 秒：选择下标 2 ，将 nums[2] 减少 1 。nums 变为 [1,0] 。
第 4 秒：标记 changeIndices[4] ，也就是标记下标 2 ，因为 nums[2] 等于 0 。
第 5 秒：选择下标 1 ，将 nums[1] 减少 1 。nums 变为 [0,0] 。
第 6 秒：标记 changeIndices[6] ，也就是标记下标 1 ，因为 nums[1] 等于 0 。
现在所有下标已被标记。
最早可以在第 6 秒标记所有下标。
所以答案是 6 。

示例 3：

Input: nums = [0,1], changeIndices = [2,2,2]
Output: -1
Explanation: 这个例子中，无法标记所有下标，因为下标 1 不在 changeIndices 中。
所以答案是 -1 。

提示：

1 <= n == nums.length <= 2000
0 <= nums[i] <= 109
1 <= m == changeIndices.length <= 2000
1 <= changeIndices[i] <= n

地址

https://leetcode.cn/contest/weekly-contest-386/problems/earliest-second-to-mark-indices-i/

题意

二分查找 + 贪心

思路

题目要求求得最早满足的时间，此时我们根据分析可以知道该时间满足单调性，即在某个时间点 $x$ 满足后，则所有大于 $x$ 的时间均满足，此时我们最重要的是可以通过二分快速的查找可以满足的最小值 $x$ 。

首先所有的 $nums[i]$ 都需要变为 $0$ 以后才可以标记，一共有 $n$ 个元素，此时 $x$ 最少需要满足 $t = \sum_{i=0}^{n-1}nums[i] + n$，如果 $x < t$ 则一定无法满足题目要求；
其次必须满足 $i\in[0,n-1]$ 必须在 $changeIndices$ 全部都要出现一次才可以。此时我们统计所有索引全部出现一次的最早时间为 $y$, 此时也必须满足 $x \ge y$；
为了方便满足题目要求，则对于每个索引来说最晚需要标记的时间即为该索引在数组中出现的最晚时间，我们统计每个索引 $i$ 在小于等于 $x$ 前提下，出现的最晚时间为 $t[i]$，然后将 $t$ 按照时间的先后进行排序，即此时对于每个索引 $i$ 实现翻转需要的时间即为 $nums[i] + 1$：
- 每个元素减少到 $0$ 需要的时间为 $nums[i]$;
- 每个元素需要标记，需要的时间为 $1$，因此总的时间即为 $nums[i] + 1$；
  我们统计当前翻转索引需要的总时间为 $need$，按照时间先后顺序当前索引出现的时间为 $t[i]$，此时必须满足 $t[i] \ge need$ 才可使得当前索引 $i$ 进行翻转，贪心的检测即可，如果可以完成全部索引的翻转，则检测成功，否则则返回不成功。

我们利用上述检测方法即可快速的检测 $x$ 时间是否可以实现全部的翻转。
复杂度分析：

时间复杂度：$O(n \log n \times \log m)$, $m,n$ 表示给定的数组的长度；
空间复杂度：$O(m)$；

代码

class Solution:
    def earliestSecondToMarkIndices(self, nums: List[int], changeIndices: List[int]) -> int:
        n, m = len(nums), len(changeIndices)
        tot, start = sum(nums), -1
        cnt = {}
        for i in range(m):
            if changeIndices[i] in cnt:
                cnt[changeIndices[i]].append(i + 1)
            else:
                cnt[changeIndices[i]] = [i + 1]
            if len(cnt)== n and start == -1:
                start = i + 1
        if start < 0 or m < tot + n:
            return -1

        def check(x):        
            if x < tot + n:
                return False
            arr = []
            for i in range(1, n + 1):
                j = bisect.bisect_right(cnt[i], x) - 1
                arr.append([cnt[i][j], i])
            arr.sort()
            need = 0
            for time, idx in arr:
                need += nums[idx - 1] + 1
                if time < need:
                    return False
            return True
        
        lo, hi = max(start, tot + n), m
        res = -1
        while lo <= hi:
            mid = (lo + hi) // 2
            if check(mid):
                res = mid
                hi = mid - 1
            else:
                lo = mid + 1
        return res

100197. 标记所有下标的最早秒数 II

给你两个下标从 1 开始的整数数组 nums 和 changeIndices ，数组的长度分别为 n 和 m 。

一开始，nums 中所有下标都是未标记的，你的任务是标记 nums 中所有下标。

从第 1 秒到第 m 秒（包括第 m 秒），对于每一秒 s ，你可以执行以下操作之一：

选择范围 [1, n] 中的一个下标 i ，并且将 nums[i] 减少 1 。
将 nums[changeIndices[s]] 设置成任意的非负整数。
选择范围 [1, n] 中的一个下标 i ，满足 nums[i] 等于 0, 并标记下标 i 。
什么也不做。

请你返回范围 [1, m] 中的一个整数，表示最优操作下，标记 nums 中所有下标的 最早秒数 ，如果无法标记所有下标，返回 -1 。

示例 1：

输入：nums = [3,2,3], changeIndices = [1,3,2,2,2,2,3]
输出：6
解释：这个例子中，我们总共有 7 秒。按照以下操作标记所有下标：
第 1 秒：将 nums[changeIndices[1]] 变为 0 。nums 变为 [0,2,3] 。
第 2 秒：将 nums[changeIndices[2]] 变为 0 。nums 变为 [0,2,0] 。
第 3 秒：将 nums[changeIndices[3]] 变为 0 。nums 变为 [0,0,0] 。
第 4 秒：标记下标 1 ，因为 nums[1] 等于 0 。
第 5 秒：标记下标 2 ，因为 nums[2] 等于 0 。
第 6 秒：标记下标 3 ，因为 nums[3] 等于 0 。
现在所有下标已被标记。
最早可以在第 6 秒标记所有下标。
所以答案是 6 。

示例 2：

输入：nums = [0,0,1,2], changeIndices = [1,2,1,2,1,2,1,2]
输出：7
解释：这个例子中，我们总共有 8 秒。按照以下操作标记所有下标：
第 1 秒：标记下标 1 ，因为 nums[1] 等于 0 。
第 2 秒：标记下标 2 ，因为 nums[2] 等于 0 。
第 3 秒：将 nums[4] 减少 1 。nums 变为 [0,0,1,1] 。
第 4 秒：将 nums[4] 减少 1 。nums 变为 [0,0,1,0] 。
第 5 秒：将 nums[3] 减少 1 。nums 变为 [0,0,0,0] 。
第 6 秒：标记下标 3 ，因为 nums[3] 等于 0 。
第 7 秒：标记下标 4 ，因为 nums[4] 等于 0 。
现在所有下标已被标记。
最早可以在第 7 秒标记所有下标。
所以答案是 7 。

示例 3：

输入：nums = [1,2,3], changeIndices = [1,2,3]
输出：-1
解释：这个例子中，无法标记所有下标，因为我们没有足够的秒数。
所以答案是 -1 。

提示：

1 <= n == nums.length <= 5000
0 <= nums[i] <= 109
1 <= m == changeIndices.length <= 5000
1 <= changeIndices[i] <= n

地址

https://leetcode.cn/contest/weekly-contest-386/problems/earliest-second-to-mark-indices-ii/

题意

二分 + 贪心算法

思路

t4 确实很难，但是到目前为止也还没有将该题弄的特别明白。t4 加了一个特殊的条件即当出现该索引 $i$ 时，可以在 $1$ 个时间内将该元素变为 $0$，此时情况就变得比较复杂了，当然大方向还是二分法，但是如何利用好二分法，需要值得仔细研究。 T4 全服不到 50 人 AK，应该是难度创新高了，非常经典的反悔贪心算法。

由于每个元素既可以使用方法 $1$ 通过 $nums[i]$ 时间将元素 $nums[i]$ 变为 $0$;
由于每个索引还可以使用方法 $2$ 通过 $1$ 天内将元素 $nums[i]$ 变为 $0$，当然对于每个元素来说，要么采用方法 $1$ 要么采用方法 $2$；
题目的关键点在于对于每个索引到底是该采用方法 $1$ 还是采用方法 $2$，同时还要分配 $n$ 天出来用于每个元素的标记，且满足标记的时间在归 $0$ 的时间之后；但实际过程计算过程中又存在几个问题，假设我们把所有时间都用来做方法二的归零后，但是可能会导致后期标记的时间不够，因此还是很复杂；
利用贪心算法，利用 $cnt$ 统计相关右边可以用来留来作为标记的时间，则会遇到以下几种情况：
- 假设当前元素 $i$ 且当前元素 $i$ 并不是该元素在数组中第一次出现，则此时我们可以将 $cnt + 1$，可以将 $cnt$ 预留；
- 假设当前元素 $i$ 且当前元素 $i$ 满足 $nums[i] \le 1$, 此时该元素只需要给其预留位置即可，因为它可以在任意地方进行归零与标记操作即可；
- 假设当前 $cnt = 0$, 则此时没有多余的时间用来讲当前元素进行标记。

复杂度分析：

时间复杂度：$O(n log n \times \log m)$，其中 $m,n$ 表示数组的长度。
空间复杂度：$O(n)$，其中 $n$ 表示数组的长度。

代码

class Solution:
    def earliestSecondToMarkIndices(self, nums: List[int], changeIndices: List[int]) -> int:
        n, m = len(nums), len(changeIndices)
        total = n + sum(nums)
        pos = [-1] * n
        for t in range(m - 1, -1, -1):
            pos[changeIndices[t] - 1] = t

        def check(mx: int) -> bool:
            # 表示右侧可以消耗的时间
            cnt = 0
            slow = total  # 慢速复习 + 考试所需天数
            h = []
            for t in range(mx - 1, -1, -1):
                i = changeIndices[t] - 1
                v = nums[i]
                if v <= 1 or t != pos[i]:
                    cnt += 1  # 留给左边，用来快速复习/考试
                    continue
                if cnt == 0:
                    if not h or v <= h[0]:
                        cnt += 1  # 留给左边，用来快速复习/考试
                        continue
                    slow += heappop(h) + 1
                    cnt += 2  # 反悔：一天快速复习，一天考试
                slow -= v + 1
                cnt -= 1  # 快速复习，然后消耗一天来考试
                heappush(h, v)
            return cnt >= slow  # 剩余天数不能慢速复习+考试

        lo, hi = 1, m
        res = -1
        while lo <= hi:
            mid = (lo + hi) // 2
            if check(mid):
                res = mid
                hi = mid - 1
            else:
                lo = mid + 1
        return res

欢迎关注和打赏，感谢支持！

关注我的博客: https://mike-box.github.io/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu

Tags: 题解力扣周赛赛

← leetcode contest 380 leetcode contest 387 →

扫描二维码，分享此文章