leetcode contest 383 感觉非常常规的题目,毫无新意的题目
3028. 边界上的蚂蚁 边界上有一只蚂蚁,它有时向 左 走,有时向 右 走。
给你一个 非零 整数数组 nums 。蚂蚁会按顺序读取 nums 中的元素,从第一个元素开始直到结束。每一步,蚂蚁会根据当前元素的值移动:
如果 nums[i] < 0 ,向 左 移动 -nums[i]单位。
如果 nums[i] > 0 ,向 右 移动 nums[i]单位。
返回蚂蚁 返回 到边界上的次数。
注意:
边界两侧有无限的空间。
只有在蚂蚁移动了 |nums[i]| 单位后才检查它是否位于边界上。换句话说,如果蚂蚁只是在移动过程中穿过了边界,则不会计算在内。
示例 1:
输入:nums = [2,3,-5] 输出:1 解释:第 1 步后,蚂蚁距边界右侧 2 单位远。 第 2 步后,蚂蚁距边界右侧 5 单位远。 第 3 步后,蚂蚁位于边界上。 所以答案是 1 。
示例 2:
输入:nums = [3,2,-3,-4] 输出:0 解释:第 1 步后,蚂蚁距边界右侧 3 单位远。 第 2 步后,蚂蚁距边界右侧 5 单位远。 第 3 步后,蚂蚁距边界右侧 2 单位远。 第 4 步后,蚂蚁距边界左侧 2 单位远。 蚂蚁从未返回到边界上,所以答案是 0 。
提示:
1 <= nums.length <= 100-10 <= nums[i] <= 10nums[i] != 0
地址 https://leetcode.cn/contest/weekly-contest-383/problems/ant-on-the-boundary/
题意 直接模拟即可
思路
题目只要求到达原点的次数,我们直接累加所有元素,统计出现 $0$ 的次数即可;
复杂度分析:
时间复杂度:$O(n)$,其中 $n$ 表示给定数组的长度。
空间复杂度:$O(1)$。
代码 class Solution : def returnToBoundaryCount (self, nums: List [int ] ) -> int : ans, tot = 0 , 0 for x in nums: tot += x if tot == 0 : ans += 1 return ans
3031. 将单词恢复初始状态所需的最短时间 II 给你一个下标从 0 开始的字符串 word 和一个整数 k 。
在每一秒,你必须执行以下操作:
移除 word 的前 k 个字符。
在 word 的末尾添加 k 个任意字符。
注意 添加的字符不必和移除的字符相同。但是,必须在每一秒钟都执行 两种 操作。
返回将 word 恢复到其 初始 状态所需的 最短 时间(该时间必须大于零)。
示例 1:
输入:word = "abacaba", k = 3 输出:2 解释: 第 1 秒,移除 word 的前缀 "aba",并在末尾添加 "bac" 。因此,word 变为 "cababac"。 第 2 秒,移除 word 的前缀 "cab",并在末尾添加 "aba" 。因此,word 变为 "abacaba" 并恢复到始状态。 可以证明,2 秒是 word 恢复到其初始状态所需的最短时间。
示例 2:
输入:word = "abacaba", k = 4 输出:1 解释: 第 1 秒,移除 word 的前缀 "abac",并在末尾添加 "caba" 。因此,word 变为 "abacaba" 并恢复到初始状态。 可以证明,1 秒是 word 恢复到其初始状态所需的最短时间。
示例 3:
输入:word = "abcbabcd", k = 2 输出:4 解释: 每一秒,我们都移除 word 的前 2 个字符,并在 word 末尾添加相同的字符。 4 秒后,word 变为 "abcbabcd" 并恢复到初始状态。 可以证明,4 秒是 word 恢复到其初始状态所需的最短时间。
提示:
1 <= word.length <= 1061 <= k <= word.lengthword仅由小写英文字母组成。
地址 https://leetcode.cn/contest/weekly-contest-383/problems/minimum-time-to-revert-word-to-initial-state-ii/
题意 字符串哈希算法
思路
题目本身没啥难度,主要就是找到给定字符串的后缀与前缀匹配的最大长度即可,此时最简单的办法就是字符串哈希算法,我们可以很快的求出每个子字符串的哈希值然后比较即可,熟悉 KR 算法来说,这个题目毫无难度可言。
复杂度分析:
时间复杂度:$O(n)$, $n$ 表示给定字符串 $s$ 的长度;
空间复杂度:$O(n)$;
代码 class Solution : def minimumTimeToInitialState (self, word: str, k: int ) -> int : mod = 10 **9 + 7 base = 31 n = len (word) h = [1 ] * (n + 1 ) arr = [0 ] * (n + 1 ) for i in range (n): h[i + 1 ] = (h[i] * base) % mod arr[i + 1 ] = (arr[i] * base + ord (word[i]) - ord ('a' )) % mod def get (i, j): return (arr[j + 1 ] - arr[i] * h[j - i + 1 ] % mod + mod) % mod ans = 1 for i in range (k, n, k): if get (0 , n - 1 - i) == get (i, n - 1 ): return ans ans += 1 return ans
3030. 找出网格的区域平均强度 给你一个下标从 0 开始、大小为 m x n 的网格 image ,表示一个灰度图像,其中 image[i][j] 表示在范围 [0..255] 内的某个像素强度。另给你一个 非负 整数 threshold 。
如果 image[a][b] 和 image[c][d] 满足 |a - c| + |b - d| == 1 ,则称这两个像素是 相邻像素 。
区域 是一个 3 x 3 的子网格,且满足区域中任意两个 相邻 像素之间,像素强度的 绝对差 小于或等于 threshold 。
区域 内的所有像素都认为属于该区域,而一个像素 可以 属于 多个 区域。
你需要计算一个下标从 0 开始、大小为 m x n 的网格 result ,其中 result[i][j] 是 image[i][j] 所属区域的 平均 强度,向下取整 到最接近的整数。如果 image[i][j] 属于多个区域,result[i][j] 是这些区域的 “取整后的平均强度” 的 平均值 ,也 向下取整 到最接近的整数。如果 image[i][j] 不属于任何区域,则 result[i][j] 等于 image[i][j] 。
返回网格 result 。
示例 1:
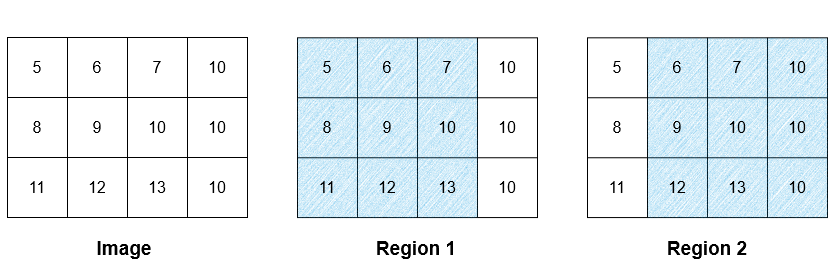
输入:image = [[5,6,7,10],[8,9,10,10],[11,12,13,10]], threshold = 3 输出:[[9,9,9,9],[9,9,9,9],[9,9,9,9]] 解释:图像中存在两个区域,如图片中的阴影区域所示。第一个区域的平均强度为 9 ,而第二个区域的平均强度为 9.67 ,向下取整为 9 。两个区域的平均强度为 (9 + 9) / 2 = 9 。由于所有像素都属于区域 1 、区域 2 或两者,因此 result 中每个像素的强度都为 9 。 注意,在计算多个区域的平均值时使用了向下取整的值,因此使用区域 2 的平均强度 9 来进行计算,而不是 9.67 。
示例 2:
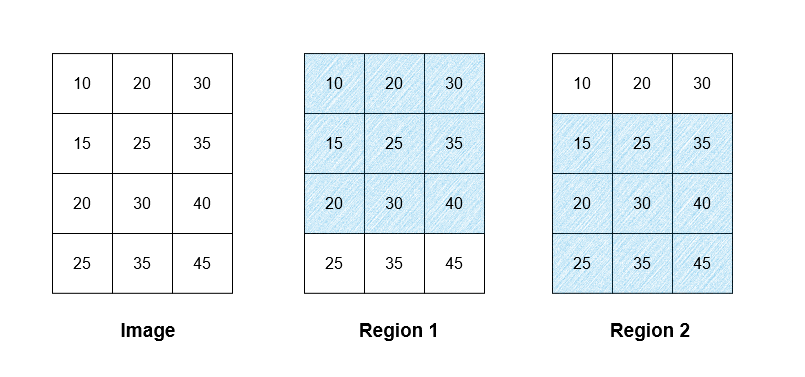
输入:image = [[10,20,30],[15,25,35],[20,30,40],[25,35,45]], threshold = 12 输出:[[25,25,25],[27,27,27],[27,27,27],[30,30,30]] 解释:图像中存在两个区域,如图片中的阴影区域所示。第一个区域的平均强度为 25 ,而第二个区域的平均强度为 30 。两个区域的平均强度为 (25 + 30) / 2 = 27.5 ,向下取整为 27 。图像中第 0 行的所有像素属于区域 1 ,因此 result 中第 0 行的所有像素为 25 。同理,result 中第 3 行的所有像素为 30 。图像中第 1 行和第 2 行的像素属于区域 1 和区域 2 ,因此它们在 result 中的值为 27 。
示例 3:
输入:image = [[5,6,7],[8,9,10],[11,12,13]], threshold = 1 输出:[[5,6,7],[8,9,10],[11,12,13]] 解释:图像中不存在任何区域,因此对于所有像素,result[i][j] == image[i][j] 。
提示:
3 <= n, m <= 5000 <= image[i][j] <= 2550 <= threshold <= 255
地址 https://leetcode.cn/contest/weekly-contest-383/problems/find-the-grid-of-region-average/
题意
前缀和
思路
题目本身比较简单,但是处理起来稍微复杂了一些。题目本身没有任何难度,就是处理起来稍微有点复杂,需要处理各种细节。
复杂度分析:
时间复杂度:$O(mn)$,其中 $mn$ 表示给定矩阵的行数与列数。
空间复杂度:$O(n)$,其中 $n$ 表示给定的数组的长度。
代码 class Solution : def resultGrid (self, image: List [List [int ]], threshold: int ) -> List [List [int ]]: m = len (image) n = len (image[0 ]) cnt = [[0 ] * (n + 1 ) for _ in range (m + 1 )] tot = [[0 ] * n for _ in range (m)] psum = [[0 ] * n for _ in range (m)] for i in range (m): for j in range (n): cnt[i + 1 ][j + 1 ] = cnt[i + 1 ][j] + cnt[i][j + 1 ] + image[i][j] - cnt[i][j] def check (i, j ): if i < 0 or j < 0 or i + 2 >= m or j + 2 >= n: return False for r in range (3 ): for c in range (3 ): if c > 0 and abs (image[i + r][j + c] - image[i + r][j + c - 1 ]) > threshold: return False if r > 0 and abs (image[i + r][j + c] - image[i + r - 1 ][j + c]) > threshold: return False return True def get (i, j ): return cnt[i + 3 ][j + 3 ] - cnt[i + 3 ][j] - cnt[i][j + 3 ] + cnt[i][j] res = [[0 ] * n for _ in range (m)] for i in range (m): for j in range (n): if check(i, j): for x in range (3 ): for y in range (3 ): tot[i + x][j + y] += 1 psum[i + x][j + y] += get(i, j) // 9 if tot[i][j] == 0 : res[i][j] = image[i][j] else : res[i][j] = psum[i][j] // tot[i][j] return res
3031. 将单词恢复初始状态所需的最短时间 II 给你一个下标从 0 开始的字符串 word 和一个整数 k 。
在每一秒,你必须执行以下操作:
移除 word 的前 k 个字符。
在 word 的末尾添加 k 个任意字符。
注意 添加的字符不必和移除的字符相同。但是,必须在每一秒钟都执行 两种 操作。
返回将 word 恢复到其 初始 状态所需的 最短 时间(该时间必须大于零)。
示例 1:
输入:word = "abacaba", k = 3 输出:2 解释: 第 1 秒,移除 word 的前缀 "aba",并在末尾添加 "bac" 。因此,word 变为 "cababac"。 第 2 秒,移除 word 的前缀 "cab",并在末尾添加 "aba" 。因此,word 变为 "abacaba" 并恢复到始状态。 可以证明,2 秒是 word 恢复到其初始状态所需的最短时间。
示例 2:
输入:word = "abacaba", k = 4 输出:1 解释: 第 1 秒,移除 word 的前缀 "abac",并在末尾添加 "caba" 。因此,word 变为 "abacaba" 并恢复到初始状态。 可以证明,1 秒是 word 恢复到其初始状态所需的最短时间。
示例 3:
输入:word = "abcbabcd", k = 2 输出:4 解释: 每一秒,我们都移除 word 的前 2 个字符,并在 word 末尾添加相同的字符。 4 秒后,word 变为 "abcbabcd" 并恢复到初始状态。 可以证明,4 秒是 word 恢复到其初始状态所需的最短时间。
提示:
1 <= word.length <= 1061 <= k <= word.lengthword仅由小写英文字母组成。
地址 https://leetcode.cn/contest/weekly-contest-383/problems/minimum-time-to-revert-word-to-initial-state-ii/
题意
字符串哈希算法
思路
题目本身没啥难度,主要就是找到给定字符串的后缀与前缀匹配的最大长度即可,此时最简单的办法就是字符串哈希算法,我们可以很快的求出每个子字符串的哈希值然后比较即可,熟悉 KR 算法来说,这个题目毫无难度可言。
复杂度分析:
时间复杂度:$O(n)$, $n$ 表示给定字符串 $s$ 的长度;
空间复杂度:$O(n)$;
代码 [sol1-C++] class Solution : def minimumTimeToInitialState (self, word: str, k: int ) -> int : mod = 10 **9 + 7 base = 31 n = len (word) h = [1 ] * (n + 1 ) arr = [0 ] * (n + 1 ) for i in range (n): h[i + 1 ] = (h[i] * base) % mod arr[i + 1 ] = (arr[i] * base + ord (word[i]) - ord ('a' )) % mod def get (i, j): return (arr[j + 1 ] - arr[i] * h[j - i + 1 ] % mod + mod) % mod ans = 1 for i in range (k, n, k): if get (0 , n - 1 - i) == get (i, n - 1 ): return ans ans += 1 return ans
欢迎关注和打赏,感谢支持!