leetcode biweekly contest 123

双周赛质量不错，好久没有更新题解了，需要加快进度更新题解。

3024. 三角形类型 II

给你一个下标从 0 开始长度为 3 的整数数组 nums ，需要用它们来构造三角形。

• 如果一个三角形的所有边长度相等，那么这个三角形称为 equilateral 。
• 如果一个三角形恰好有两条边长度相等，那么这个三角形称为 isosceles 。
• 如果一个三角形三条边的长度互不相同，那么这个三角形称为 scalene 。

如果这个数组无法构成一个三角形，请你返回字符串 "none" ，否则返回一个字符串表示这个三角形的类型。

示例 1：

输入：nums = [3,3,3]
输出："equilateral"
解释：由于三条边长度相等，所以可以构成一个等边三角形，返回 "equilateral" 。

示例 2：

输入：nums = [3,4,5]
输出："scalene"
解释：
nums[0] + nums[1] = 3 + 4 = 7 ，大于 nums[2] = 5 。
nums[0] + nums[2] = 3 + 5 = 8 ，大于 nums[1] = 4 。
nums[1] + nums[2] = 4 + 5 = 9 ，大于 nums[0] = 3 。
由于任意两边纸盒都大于第三边，所以可以构成一个三角形。
因为三条边的长度互不相等，所以返回 "scalene" 。

提示：

• nums.length == 3
• 1 <= nums[i] <= 100

地址

https://leetcode.cn/contest/biweekly-contest-123/problems/type-of-triangle-ii/

题意

直接模拟即可

思路

1. 主要判断三角形的形状，分为以下几步：
   • 首先检测三角形是否正常；
   • 其次检测三角形的形状；
2. 复杂度分析：

• 时间复杂度：$O(1)$。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def triangleType(self, nums: List[int]) -> str:
        nums.sort()
        a, b, c = nums[0], nums[1], nums[2]
        if a + b <= c:
            return "none"
        elif a == b and b == c:
            return "equilateral"
        elif a == b or b == c:
            return "isosceles"
        else:
            return "scalene"

3025. 人员站位的方案数 I

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。

我们定义 x 轴的正方向为 右 （x 轴递增的方向），x 轴的负方向为 左 （x 轴递减的方向）。类似的，我们定义 y 轴的正方向为 上 （y 轴递增的方向），y 轴的负方向为 下 （y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 liupengsay 和小羊肖恩 。你需要确保每个点处 恰好 有 一个 人。同时，liupengsay 想跟小羊肖恩单独玩耍，所以 liupengsay 会以 liupengsay 的坐标为 左上角 ，小羊肖恩的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能 不 包含任何区域，也就是说围栏可能是一条线段）。如果围栏的 内部 或者 边缘 上有任何其他人，liupengsay 都会难过。

请你在确保 liupengsay 不会 难过的前提下，返回 liupengsay 和小羊肖恩可以选择的 点对 数目。

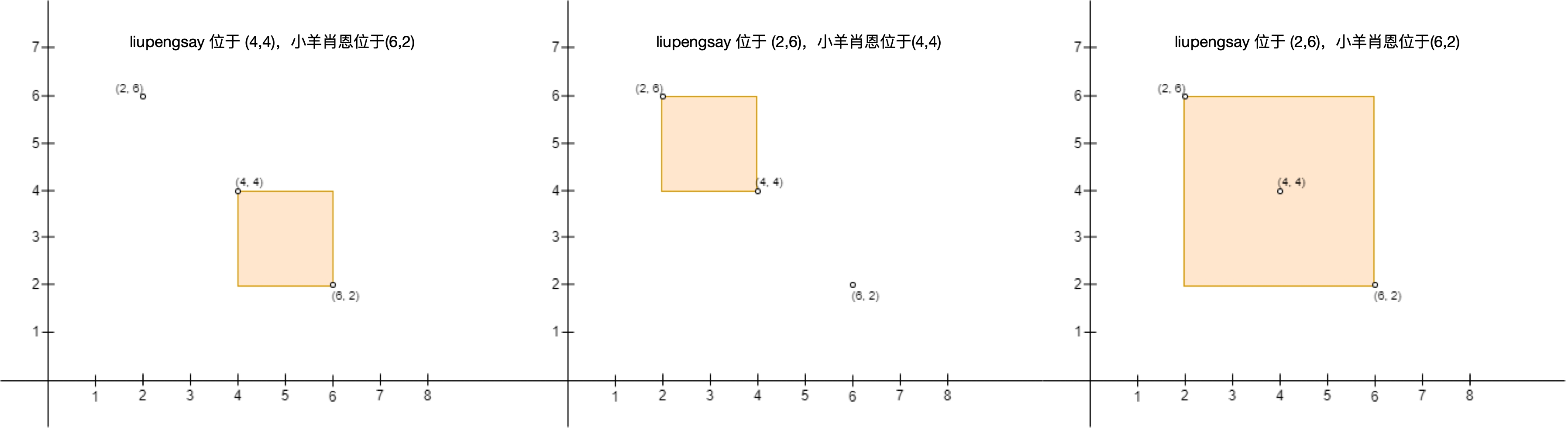
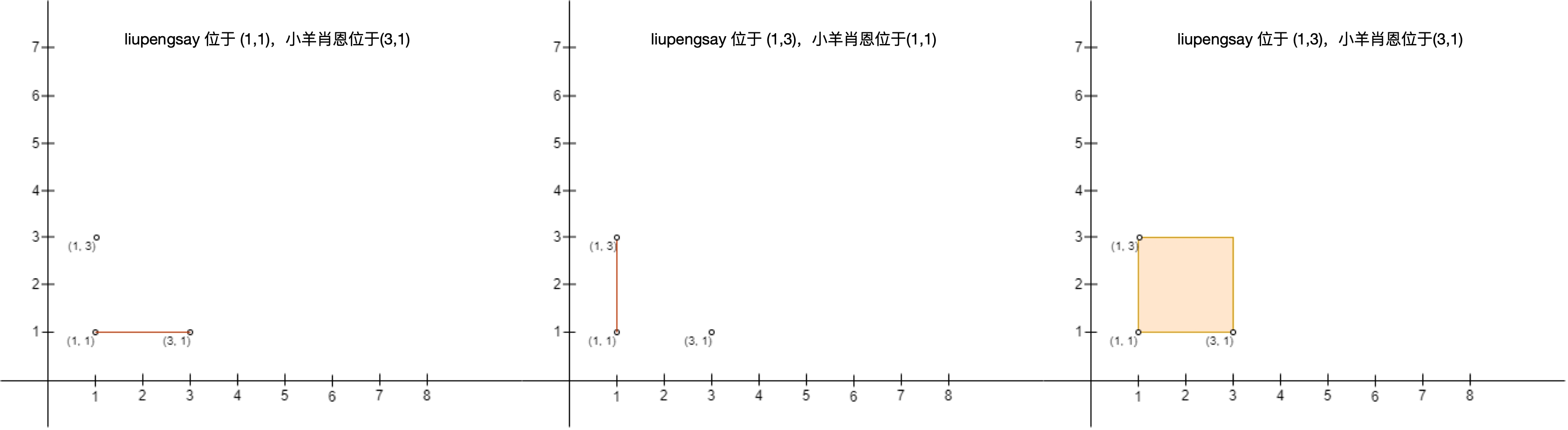
注意，liupengsay 建立的围栏必须确保 liupengsay 的位置是矩形的左上角，小羊肖恩的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，liupengsay 都不能建立围栏，原因如下：

• 图一中，liupengsay 在 (3, 3) 且小羊肖恩在 (1, 1) ，liupengsay 的位置不是左上角且小羊肖恩的位置不是右下角。
• 图二中，liupengsay 在 (1, 3) 且小羊肖恩在 (1, 1) ，小羊肖恩的位置不是在围栏的右下角。

示例 1：

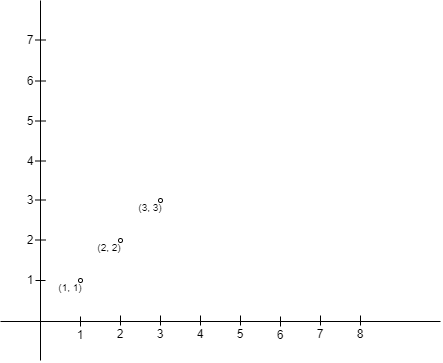
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 liupengsay 的围栏以 liupengsay 的位置为左上角且小羊肖恩的位置为右下角。所以我们返回 0 。

示例 2：

输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (4, 4) ，小羊肖恩站在 (6, 2) 。
- liupengsay 站在 (2, 6) ，小羊肖恩站在 (4, 4) 。
不能安排 liupengsay 站在 (2, 6) 且小羊肖恩站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

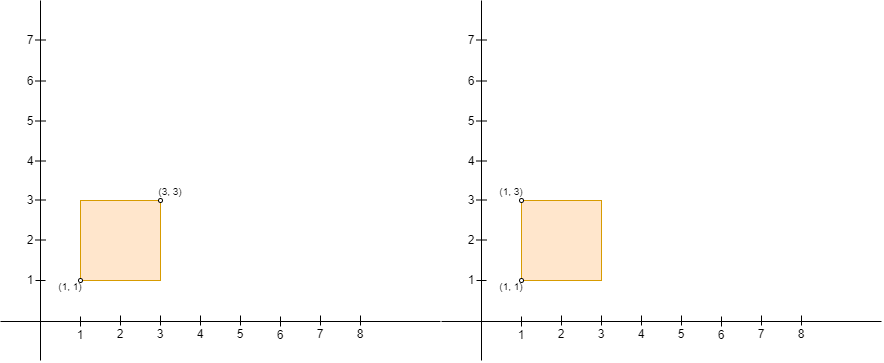
示例 3：

输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (1, 1) ，小羊肖恩站在 (3, 1) 。
- liupengsay 站在 (1, 3) ，小羊肖恩站在 (1, 1) 。
不能安排 liupengsay 站在 (1, 3) 且小羊肖恩站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

提示：

• 2 <= n <= 50
• points[i].length == 2
• 0 <= points[i][0], points[i][1] <= 50
• points[i] 点对两两不同。

地址

https://leetcode.cn/contest/biweekly-contest-123/problems/find-the-number-of-ways-to-place-people-i/

题意

枚举

思路

1. 题目本意让我找到点对 $p_1,p_2$，且满足 $p1$ 在左上角，$p_2$ 在右下角，即 $p1$ 横坐标小于等于 $p2$ 的横坐标，$p1$ 的纵坐标大于等于 $p2$ 的纵坐标，且二者构成的矩形中没有其他点。此时我们首先想到的是将所有的点按照横坐标进行排序，横坐标相同时按照纵坐标从大到小排序，假设当前遍历第 $i$ 个点，则此时只能在索引 $i$ 之后的点可以与之构成合法的点对。我们依次遍历两个点对 $(i，j)$, 但是保证两个点对构成的矩形之间不包含其他点？设两个点分别为 $(x_i,y_i),(x_j,y_j)$，此时需要满足:
   • $x_i \le x_j,y_i \ge y_j$;
   • 对于横坐标处于区间 $[x_i,x_j]$ 以外的点，此时我们不需要再讨论，重点讨论横坐标处于区间 $[x_i,xj$的点，只需要坚持是否有某个点的纵坐标处于 $[y_j,y_i]$ 即可。此时索引处在 $[i+1,j-1]$ 之间所有的点的纵坐标一定满足要么大于 $y_i$,要么小于 $y_j$，此时我们可以求出区间 $[i+1,j-1]$ 中所有点的纵坐标小于等于 $y_i$ 的最大值为 $bound$，假设此时 $bound$ 大于 $y_j$，则此时一定有某个点的纵坐标处于区间 $[y_j,y_i]$ 中。
2. 复杂度分析：

• 时间复杂度：$O(n^2)$, $n$ 表示给定数组的长度；
• 空间复杂度：$O(1)$；

代码

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        res = 0
        points.sort(key=lambda x: (x[0], -x[1]))
        for i, (_, y0) in enumerate(points):
            bound = -inf
            for _, y1 in points[i + 1:]:
                if y1 <= y0:
                    if bound < y1:
                        res += 1
                    bound = max(y1, bound)
        return res

3026. 最大好子数组和

给你一个长度为 n 的数组 nums 和一个 正 整数 k 。

如果 nums 的一个子数组中，第一个元素和最后一个元素 差的绝对值恰好 为 k ，我们称这个子数组为 好 的。换句话说，如果子数组 nums[i..j] 满足 |nums[i] - nums[j]| == k ，那么它是一个好子数组。

请你返回 nums 中 好 子数组的 最大 和，如果没有好子数组，返回 0 。

示例 1：

输入：nums = [1,2,3,4,5,6], k = 1
输出：11
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 1 。好子数组有 [1,2] ，[2,3] ，[3,4] ，[4,5] 和 [5,6] 。最大子数组和为 11 ，对应的子数组为 [5,6] 。

示例 2：

输入：nums = [-1,3,2,4,5], k = 3
输出：11
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 3 。好子数组有 [-1,3,2] 和 [2,4,5] 。最大子数组和为 11 ，对应的子数组为 [2,4,5] 。

示例 3：

输入：nums = [-1,-2,-3,-4], k = 2
输出：-6
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 2 。好子数组有 [-1,-2,-3] 和 [-2,-3,-4] 。最大子数组和为 -6 ，对应的子数组为 [-1,-2,-3] 。

提示：

• 2 <= nums.length <= 105
• -109 <= nums[i] <= 109
• 1 <= k <= 109

地址

https://leetcode.cn/contest/biweekly-contest-123/problems/maximum-good-subarray-sum/

题意

前缀和

思路

1. 题目要求找到的字数的第一个元素与最后一个元素的差值的绝对值恰好为 $k$，假设此时的元素为 $x$，则我们需要找到数组中元素为 $x-k,x+k$ 的位置，假设当前为的前缀和为 $sum[i]$，此时我们只需要找到值等于 $x-k,x+k$ 的位置 $j$，且前缀和 $sum[j-1]$ 最小，此时我们可以得到当前连续子数组的最大和即为 $sum[i] - sum[j-1]$，我们利用哈希表存储当前元素为 $x$ 且当前元素之前的所有元素的前缀和的最小值。

2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。
• 空间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。

代码

class Solution:
    def maximumSubarraySum(self, nums: List[int], k: int) -> int:
        n = len(nums)
        res = -inf
        psum = [0] * (n + 1)
        for i, x in enumerate(nums):
            psum[i + 1] = psum[i] + x
        
        cnt = {}
        for i, x in enumerate(nums):
            if x - k in cnt:
                res = max(res, psum[i + 1] - cnt[x - k])
            if x + k in cnt:
                res = max(res, psum[i + 1] - cnt[x + k])
            if x not in cnt:
                cnt[x] = psum[i]
            else:
                cnt[x] = min(cnt[x], psum[i])
        return res if res != -inf else 0

3207. 人员站位的方案数 II

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。

我们定义 x 轴的正方向为 右 （x 轴递增的方向），x 轴的负方向为 左 （x 轴递减的方向）。类似的，我们定义 y 轴的正方向为 上 （y 轴递增的方向），y 轴的负方向为 下 （y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 liupengsay 和小羊肖恩 。你需要确保每个点处 恰好 有 一个 人。同时，liupengsay 想跟小羊肖恩单独玩耍，所以 liupengsay 会以 liupengsay 的坐标为 左上角 ，小羊肖恩的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能 不 包含任何区域，也就是说围栏可能是一条线段）。如果围栏的 内部 或者 边缘 上有任何其他人，liupengsay 都会难过。

请你在确保 liupengsay 不会 难过的前提下，返回 liupengsay 和小羊肖恩可以选择的 点对 数目。

注意，liupengsay 建立的围栏必须确保 liupengsay 的位置是矩形的左上角，小羊肖恩的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，liupengsay 都不能建立围栏，原因如下：

• 图一中，liupengsay 在 (3, 3) 且小羊肖恩在 (1, 1) ，liupengsay 的位置不是左上角且小羊肖恩的位置不是右下角。
• 图二中，liupengsay 在 (1, 3) 且小羊肖恩在 (1, 1) ，小羊肖恩的位置不是在围栏的右下角。

示例 1：

输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 liupengsay 的围栏以 liupengsay 的位置为左上角且小羊肖恩的位置为右下角。所以我们返回 0 。

示例 2：

输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (4, 4) ，小羊肖恩站在 (6, 2) 。
- liupengsay 站在 (2, 6) ，小羊肖恩站在 (4, 4) 。
不能安排 liupengsay 站在 (2, 6) 且小羊肖恩站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

示例 3：

输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (1, 1) ，小羊肖恩站在 (3, 1) 。
- liupengsay 站在 (1, 3) ，小羊肖恩站在 (1, 1) 。
不能安排 liupengsay 站在 (1, 3) 且小羊肖恩站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

提示：

• 2 <= n <= 1000
• points[i].length == 2
• -109 <= points[i][0], points[i][1] <= 109
• points[i] 点对两两不同。

地址

https://leetcode.cn/contest/biweekly-contest-123/problems/find-the-number-of-ways-to-place-people-ii/

题意

枚举

思路

1. 题目本意让我找到点对 $p_1,p_2$，且满足 $p1$ 在左上角，$p_2$ 在右下角，即 $p1$ 横坐标小于等于 $p2$ 的横坐标，$p1$ 的纵坐标大于等于 $p2$ 的纵坐标，且二者构成的矩形中没有其他点。此时我们首先想到的是将所有的点按照横坐标进行排序，横坐标相同时按照纵坐标从大到小排序，假设当前遍历第 $i$ 个点，则此时只能在索引 $i$ 之后的点可以与之构成合法的点对。我们依次遍历两个点对 $(i，j)$, 但是保证两个点对构成的矩形之间不包含其他点？设两个点分别为 $(x_i,y_i),(x_j,y_j)$，此时需要满足:

   • $x_i \le x_j,y_i \ge y_j$;
   • 对于横坐标处于区间 $[x_i,x_j]$ 以外的点，此时我们不需要再讨论，重点讨论横坐标处于区间 $[x_i,xj$的点，只需要坚持是否有某个点的纵坐标处于 $[y_j,y_i]$ 即可。此时索引处在 $[i+1,j-1]$ 之间所有的点的纵坐标一定满足要么大于 $y_i$,要么小于 $y_j$，此时我们可以求出区间 $[i+1,j-1]$ 中所有点的纵坐标小于等于 $y_i$ 的最大值为 $bound$，假设此时 $bound$ 大于 $y_j$，则此时一定有某个点的纵坐标处于区间 $[y_j,y_i]$ 中。

   比较坑的是比赛的时候用的二分查找，没有继续优化，赛后竟然超时了。

2. 复杂度分析：

• 时间复杂度：$O(n^2)$, $n$ 表示给定数组的长度；
• 空间复杂度：$O(1)$；

代码

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        res = 0
        points.sort(key=lambda x: (x[0], -x[1]))
        for i, (_, y0) in enumerate(points):
            bound = -inf
            for _, y1 in points[i + 1:]:
                if y1 <= y0:
                    if bound < y1:
                        res += 1
                    bound = max(y1, bound)
        return res

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu