leetcode contest 379

前三题可能就是简单题目， t4 构造题目确实比较难

100170. 对角线最长的矩形的面积

给你一个下标从 0 开始的二维整数数组 dimensions。

对于所有下标 i（0 <= i < dimensions.length），dimensions[i][0] 表示矩形 i 的长度，而 dimensions[i][1] 表示矩形 i 的宽度。

返回对角线最 长 的矩形的 面积 。如果存在多个对角线长度相同的矩形，返回面积最 大 的矩形的面积。

示例 1：

输入：dimensions = [[9,3],[8,6]]
输出：48
解释：
下标 = 0，长度 = 9，宽度 = 3。对角线长度 = sqrt(9 * 9 + 3 * 3) = sqrt(90) ≈ 9.487。
下标 = 1，长度 = 8，宽度 = 6。对角线长度 = sqrt(8 * 8 + 6 * 6) = sqrt(100) = 10。
因此，下标为 1 的矩形对角线更长，所以返回面积 = 8 * 6 = 48。

示例 2：

输入：dimensions = [[3,4],[4,3]]
输出：12
解释：两个矩形的对角线长度相同，为 5，所以最大面积 = 12。

提示：

• 1 <= dimensions.length <= 100
• dimensions[i].length == 2
• 1 <= dimensions[i][0], dimensions[i][1] <= 100

地址

https://leetcode.cn/contest/weekly-contest-379/problems/maximum-area-of-longest-diagonal-rectangle/

题意

直接模拟即可

思路

1. 这接找到对角线最长，且面积最大的矩形返回面积即可。
2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def areaOfMaxDiagonal(self, dimensions: List[List[int]]) -> int:
        x, y = 0, 0
        for w, h in dimensions:
            if w**2 + h**2 > x**2 + y**2 or w**2 + h**2 == x**2 + y**2 and w * h > x * y:
                x, y = w, h
        return x * y

100187. 捕获黑皇后需要的最少移动次数

现有一个下标从 0 开始的 8 x 8 棋盘，上面有 3 枚棋子。

给你 6 个整数 a 、b 、c 、d 、e 和 f ，其中：

• (a, b) 表示白色车的位置。
• (c, d) 表示白色象的位置。
• (e, f) 表示黑皇后的位置。

假定你只能移动白色棋子，返回捕获黑皇后所需的最少移动次数。

请注意：

• 车可以向垂直或水平方向移动任意数量的格子，但不能跳过其他棋子。
• 象可以沿对角线方向移动任意数量的格子，但不能跳过其他棋子。
• 如果车或象能移向皇后所在的格子，则认为它们可以捕获皇后。
• 皇后不能移动。

示例 1：

输入：a = 1, b = 1, c = 8, d = 8, e = 2, f = 3
输出：2
解释：将白色车先移动到 (1, 3) ，然后移动到 (2, 3) 来捕获黑皇后，共需移动 2 次。
由于起始时没有任何棋子正在攻击黑皇后，要想捕获黑皇后，移动次数不可能少于 2 次。

示例 2：

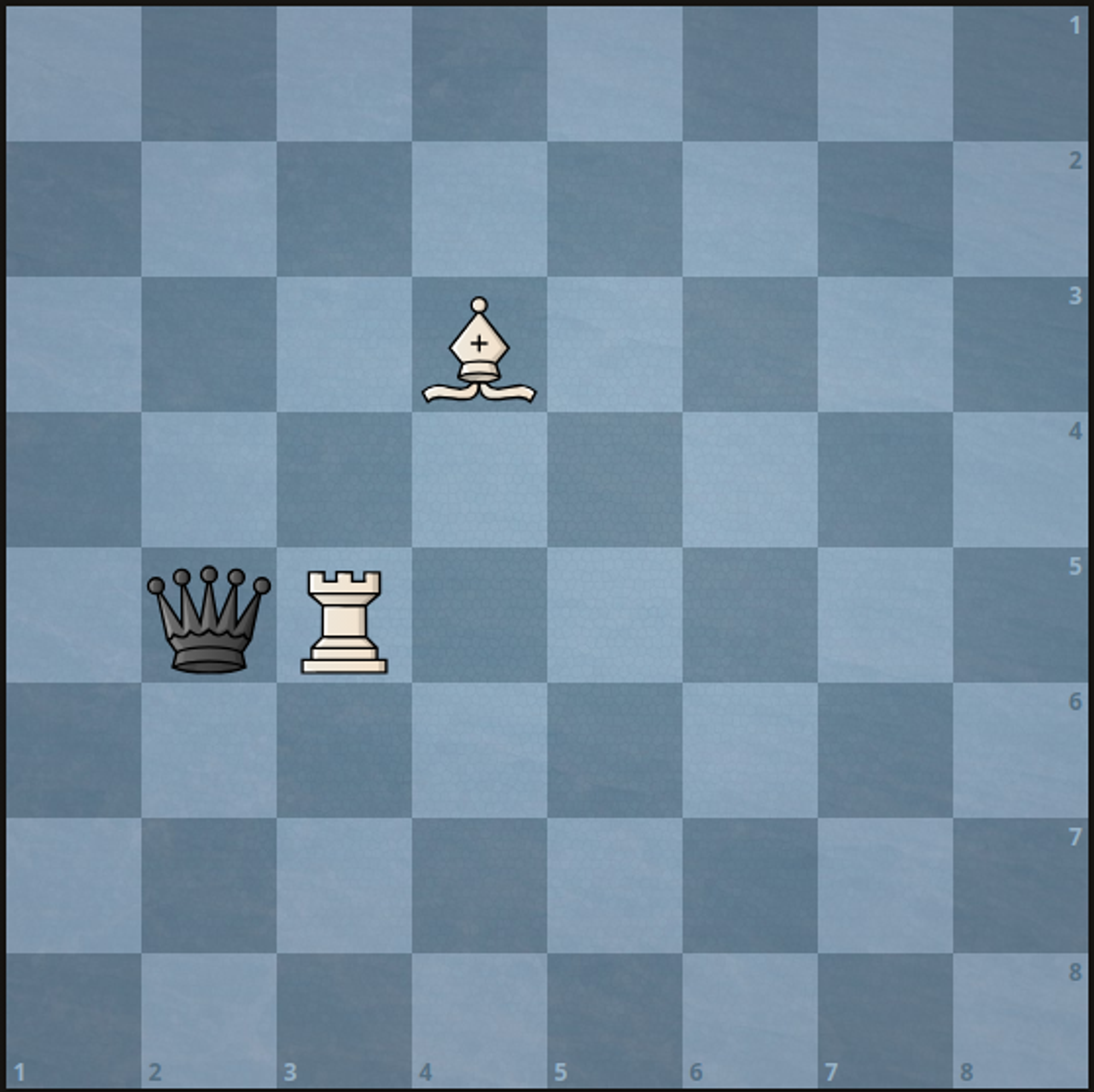
输入：a = 5, b = 3, c = 3, d = 4, e = 5, f = 2
输出：1
解释：可以通过以下任一方式移动 1 次捕获黑皇后：
- 将白色车移动到 (5, 2) 。
- 将白色象移动到 (5, 2) 。

提示：

• 1 <= a, b, c, d, e, f <= 8
• 两枚棋子不会同时出现在同一个格子上。

地址

https://leetcode.cn/contest/weekly-contest-379/problems/minimum-moves-to-capture-the-queen/

题意

构造题目

思路

1. 仔细分析一下，车或者象到皇后的移动次数最多为 $2$ 次，最少为 $1$ 次，我们找到移动次数为 $1$ 次，剩余返回 $2$ 即可，仔细分析有以下几种情况为 $1$:
   • 车与皇后在一条直线上，此时象要么不在一条直线上，要么不在二者之间，此时需要满足 :
     • $$a = e, c \neq a $$;
     • $$a = e, c = a, d \notin [\min(b,f), \max(b,f)]$$;
     • $$b = f, d \neq b $$;
     • $$a = e, d = b, c \notin [\min(a,e), \max(a,e)]$$;
   • 象与皇后在一条直线上，此时车要么不在一条直线上，要么不在二者之间，此时需要满足；
     • $|c - e| = |b - f|, (c - e)\times(b - f) \neq (a - e)\times(d - f)$;
     • $|c - e| = |b - f|, (c - e)\times(b - f) = (a - e)\times(d - f), a\notin[\min(c,e), max(c,e)]$;
2. 复杂度分析：

• 时间复杂度：$O(1)$；
• 空间复杂度：$O(1)$；

代码

class Solution:
    def minMovesToCaptureTheQueen(self, a: int, b: int, c: int, d: int, e: int, f: int) -> int:
        if a == e:
            if c != a or (c == a and (d <= min(b, f) or d >= max(b, f))):
                return 1
        if b == f:
            if d != b or (d == b and (c <= min(a, e) or c >= max(a, e))):
                return 1
        if abs(c - e) == abs(d - f):
            if (c - e) * (b - f) == (a - e) * (d - f):
                if a < min(c, e) or a > max(c, e):
                    return 1
            else:
                return 1
        return 2

100150. 移除后集合的最多元素数

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，它们的长度都是偶数 n 。

你必须从 nums1 中移除 n / 2 个元素，同时从 nums2 中也移除 n / 2 个元素。移除之后，你将 nums1 和 nums2 中剩下的元素插入到集合 s 中。

返回集合 s可能的 最多 包含多少元素。

示例 1：

输入：nums1 = [1,2,1,2], nums2 = [1,1,1,1]
输出：2
解释：从 nums1 和 nums2 中移除两个 1 。移除后，数组变为 nums1 = [2,2] 和 nums2 = [1,1] 。因此，s = {1,2} 。
可以证明，在移除之后，集合 s 最多可以包含 2 个元素。

示例 2：

输入：nums1 = [1,2,3,4,5,6], nums2 = [2,3,2,3,2,3]
输出：5
解释：从 nums1 中移除 2、3 和 6 ，同时从 nums2 中移除两个 3 和一个 2 。移除后，数组变为 nums1 = [1,4,5] 和 nums2 = [2,3,2] 。因此，s = {1,2,3,4,5} 。
可以证明，在移除之后，集合 s 最多可以包含 5 个元素。 

示例 3：

输入：nums1 = [1,1,2,2,3,3], nums2 = [4,4,5,5,6,6]
输出：6
解释：从 nums1 中移除 1、2 和 3 ，同时从 nums2 中移除 4、5 和 6 。移除后，数组变为 nums1 = [1,2,3] 和 nums2 = [4,5,6] 。因此，s = {1,2,3,4,5,6} 。
可以证明，在移除之后，集合 s 最多可以包含 6 个元素。 

提示：

• n == nums1.length == nums2.length
• 1 <= n <= 2 * 104
• n是偶数。
• 1 <= nums1[i], nums2[i] <= 109

地址

https://leetcode.cn/contest/weekly-contest-379/problems/maximum-size-of-a-set-after-removals/

题意

构造题目

思路

1. 题目看起来有一些意思，但实际也是一个构造题目，由于题目要求构造出现不同的元素尽可能的多，我们需要将数组中的元素分为三类：

   • 只出现在数组 $1$ 的元素，且不出现在数组 $2$ 中的元素数目为 $c_1$;
   • 只出现在数组 $2$ 的元素，且不出现在数组 $1$ 中的元素数目为 $c_2$;
   • 同时出现在数组 $1$ 与数组 $2$ 中的元素数目为 $c$;

   根据以上分析，假设两个数组合并，最多只能有 $c_1 + c_2 + c$ 个元素，我们从数组中挑出 $\frac{n}{2}$ 个，从数组 $2$ 中挑出 $\frac{n}{2}$ 个；

2. 根据 $1$ 的分析，我们首先尽量选择出现在 $1$ 个数组中的元素，此时数组 $1$ 中先选择 $x = \min(c_1,\frac{n}{2})$ 个元素，数组 $2$ 中先选择 $y = \min(c_2,\frac{n}{2})$ 个元素，剩余不足 $n$ 个的元素只能从 $c$ 中选择，因此最多的数目即为 $\min(x + y + c, n)$ 个元素；

3. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。
• 空间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。

代码

class Solution:
    def maximumSetSize(self, nums1: List[int], nums2: List[int]) -> int:
        cnt1, cnt2 = set(nums1), set(nums2)
        c1 = sum(1 for x in cnt1 if x not in cnt2)
        c2 = sum(1 for x in cnt2 if x not in cnt1)
        c = len(cnt1) - c1
        return min(len(nums1), min(c1, len(nums1) // 2) + min(c2, len(nums1) // 2) + c)

100154. 执行操作后的最大分割数量

给你一个下标从 0 开始的字符串 s 和一个整数 k。

你需要执行以下分割操作，直到字符串 s 变为 空：

• 选择 s 的最长前缀，该前缀最多包含 k 个 不同 字符。
• 删除 这个前缀，并将分割数量加一。如果有剩余字符，它们在 s 中保持原来的顺序。

执行操作之 前 ，你可以将 s 中 至多一处 下标的对应字符更改为另一个小写英文字母。

在最优选择情形下改变至多一处下标对应字符后，用整数表示并返回操作结束时得到的最大分割数量。

示例 1：

输入：s = "accca", k = 2
输出：3
解释：在此示例中，为了最大化得到的分割数量，可以将 s[2] 改为 'b'。
s 变为 "acbca"。
按照以下方式执行操作，直到 s 变为空：
- 选择最长且至多包含 2 个不同字符的前缀，"acbca"。
- 删除该前缀，s 变为 "bca"。现在分割数量为 1。
- 选择最长且至多包含 2 个不同字符的前缀，"bca"。
- 删除该前缀，s 变为 "a"。现在分割数量为 2。
- 选择最长且至多包含 2 个不同字符的前缀，"a"。
- 删除该前缀，s 变为空。现在分割数量为 3。
因此，答案是 3。
可以证明，分割数量不可能超过 3。

示例 2：

输入：s = "aabaab", k = 3
输出：1
解释：在此示例中，为了最大化得到的分割数量，可以保持 s 不变。
按照以下方式执行操作，直到 s 变为空： 
- 选择最长且至多包含 3 个不同字符的前缀，"aabaab"。
- 删除该前缀，s 变为空。现在分割数量为 1。
因此，答案是 1。
可以证明，分割数量不可能超过 1。

示例 3：

输入：s = "xxyz", k = 1
输出：4
解释：在此示例中，为了最大化得到的分割数量，可以将 s[1] 改为 'a'。
s 变为 "xayz"。
按照以下方式执行操作，直到 s 变为空：
- 选择最长且至多包含 1 个不同字符的前缀，"xayz"。
- 删除该前缀，s 变为 "ayz"。现在分割数量为 1。
- 选择最长且至多包含 1 个不同字符的前缀，"ayz"。
- 删除该前缀，s 变为 "yz"，现在分割数量为 2。
- 选择最长且至多包含 1 个不同字符的前缀，"yz"。
- 删除该前缀，s 变为 "z"。现在分割数量为 3。
- 选择最且至多包含 1 个不同字符的前缀，"z"。
- 删除该前缀，s 变为空。现在分割数量为 4。
因此，答案是 4。
可以证明，分割数量不可能超过 4。

提示：

• 1 <= s.length <= 104
• s 只包含小写英文字母。
• 1 <= k <= 26

地址

https://leetcode.cn/contest/weekly-contest-379/problems/maximize-the-number-of-partitions-after-operations/

题意

暴力

思路

1. 确实没有想到太好的办法，就直接暴力枚举所有可能的状态，直接设 $dp[i][mask][flag][cnt]$ 表示当前能够获得的最大分割量，其中 $i$ 表示当前索引，$mask$ 表示当前数组末尾的二进制压缩，$flag$ 表示当前是否使用操作，$cnt$ 表示当前的状态。暴力检测即可。看了官方题解，给的方法也不太好。

2. 复杂度分析:

• 时间复杂度：$O(Cn)$，其中 $n$ 表示给定的字符串的长度；
• 空间复杂度：$O(2^C \times n)$，其中 $n$ 表示给定的字符串的长度;

代码

class Solution:

    def maxPartitionsAfterOperations(self, s: str, k: int) -> int:
        if k == 26:
            return 1
        A = list(ord(c) - ord('a') for c in s)
        n = len(A)

        @cache
        def dp(i, s, t, cur):
            if i == n:
                return cur
            s2 = s | (1 << A[i])
            res = 0
            if s2.bit_count() > k:
                res = max(res, dp(i + 1, 1 << A[i], t, cur + 1))
            else:
                res = max(res, dp(i + 1, s2, t, cur))
            if t > 0:
                for j in range(26):
                    s2 = s | (1 << j)
                    if s2.bit_count() > k:
                        res = max(res, dp(i + 1, 1 << j, t - 1, cur + 1))
                    else:
                        res = max(res, dp(i + 1, s2, t - 1, cur))
            return res
        return dp(0, 0, 1, 1)

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu