leetcode biweekly contest 120

算是比较简单的双周赛的题目了，T3 有一些思考的性质的题目，其余都是简单题目。

2970. 统计移除递增子数组的数目 I

给你一个下标从 0 开始的 正 整数数组 nums 。

如果 nums 的一个子数组满足：移除这个子数组后剩余元素 严格递增 ，那么我们称这个子数组为 移除递增 子数组。比方说，[5, 3, 4, 6, 7] 中的 [3, 4] 是一个移除递增子数组，因为移除该子数组后，[5, 3, 4, 6, 7] 变为 [5, 6, 7] ，是严格递增的。

请你返回 nums 中 移除递增 子数组的总数目。

注意 ，剩余元素为空的数组也视为是递增的。

子数组 指的是一个数组中一段连续的元素序列。

示例 1：

输入：nums = [1,2,3,4]
输出：10
解释：10 个移除递增子数组分别为：[1], [2], [3], [4], [1,2], [2,3], [3,4], [1,2,3], [2,3,4] 和 [1,2,3,4]。移除任意一个子数组后，剩余元素都是递增的。注意，空数组不是移除递增子数组。

示例 2：

输入：nums = [6,5,7,8]
输出：7
解释：7 个移除递增子数组分别为：[5], [6], [5,7], [6,5], [5,7,8], [6,5,7] 和 [6,5,7,8] 。
nums 中只有这 7 个移除递增子数组。

示例 3：

输入：nums = [8,7,6,6]
输出：3
解释：3 个移除递增子数组分别为：[8,7,6], [7,6,6] 和 [8,7,6,6] 。注意 [8,7] 不是移除递增子数组因为移除 [8,7] 后 nums 变为 [6,6] ，它不是严格递增的。

提示：

• 1 <= nums.length <= 50
• 1 <= nums[i] <= 50

地址

https://leetcode.cn/contest/biweekly-contest-120/problems/count-the-number-of-incremovable-subarrays-i/

题意

模拟

思路

1. 题目比较有意思的题目，其实我们仔细分析一下，去掉一个数组中的一个连续子数组使得数组中剩余的元素严格递增，实际我们有三种去除方法：

• 去掉数组中的前 $x$ 个元素，使得剩余元素 $nums[{x+1}\cdots{n-1}]$ 严格递增；
• 去掉数组中的后 $x$ 个元素，使得剩余元素 $nums[{0}\cdots{n-x-1}]$ 严格递增；
• 去掉数组中间的 $x$ 个元素，使得剩余元素 $nums[{0}\cdots{i}]，nums[{i+x+1}\cdots{n-1}]$ 严格递增；
  根据以上分析，我们分别检测这三种情况：
• 去掉前面的元素，此时我们求出数组后部最长的严格递增的元素数组为 $nums[r\cdots{n-1}]$，此时可以构成的严格递增子数组可以为:
  $$
  nums[r\cdots n-1] \
  nums[r + 1\cdots n-1] \
  nums[r + 2\cdots n-1] \
  \cdots \
  nums[n-1] \
  $$
  一共可以有 $n-r$ 个严格递增子数组；
• 去掉后面的元素，此时我们求出数组前部最长的严格递增的元素数组为 $nums[0\cdots{l}]$，此时可以构成的严格递增子数组可以为:
  $$
  nums[0\cdots l] \
  nums[0\cdots l-1] \
  nums[0\cdots l-2] \
  \cdots \
  nums[0] \
  $$
  一共可以有 $l + 1$ 个严格递增子数组；
• 去掉中间的元素，此时假设数组的前半分数数组为 $nums[0 \cdots l]$，后半部分数组为 $nums[r \cdots n-1]$，此时需要严格保证
  • $nums[0 \cdots l]$ 严格递增；
  • $nums[r \cdots n-1]$ 严格递增；
  • $nums[r] > nums[l]$；
    实际此时我们可以用双指针，$l$ 指向数组的前半部分结尾， $r$ 指向后半部分的开头，此时移动左侧 $l$ 后，看存在多少 $r$ 满足 $nums[r] > nums[l]$;

2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def incremovableSubarrayCount(self, nums: List[int]) -> int:
        n = len(nums)
        res = 1
        left, right = 1, n - 1
        while left < len(nums) and nums[left] > nums[left - 1]:
            left += 1
        while right >= 1 and nums[right - 1] < nums[right]:
            right -= 1
            
        if left == n:
            return (n  + 1) * n // 2
        else:
            l, r = left, n - right
            res += l + r
            i, j = 0, right
            while i < left:
                while j < n and nums[j] <= nums[i]:
                    j += 1
                res += n - j
                i += 1
        return res

2973. 树中每个节点放置的金币数目

给你一棵 n 个节点的 无向 树，节点编号为 0 到 n - 1 ，树的根节点在节点 0 处。同时给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。

给你一个长度为 n 下标从 0 开始的整数数组 cost ，其中 cost[i] 是第 i 个节点的 开销 。

你需要在树中每个节点都放置金币，在节点 i 处的金币数目计算方法如下：

• 如果节点 i 对应的子树中的节点数目小于 3 ，那么放 1 个金币。
• 否则，计算节点 i 对应的子树内 3 个不同节点的开销乘积的 最大值 ，并在节点 i 处放置对应数目的金币。如果最大乘积是 负数 ，那么放置 0 个金币。

请你返回一个长度为 n 的数组 coin ，coin[i]是节点 i 处的金币数目。

示例 1：

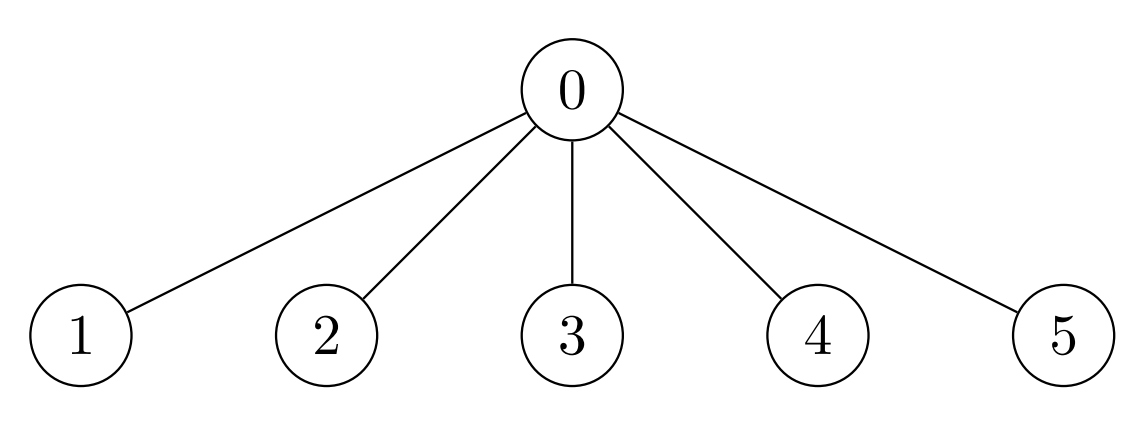
输入：edges = [[0,1],[0,2],[0,3],[0,4],[0,5]], cost = [1,2,3,4,5,6]
输出：[120,1,1,1,1,1]
解释：在节点 0 处放置 6 * 5 * 4 = 120 个金币。所有其他节点都是叶子节点，子树中只有 1 个节点，所以其他每个节点都放 1 个金币。

示例 2：

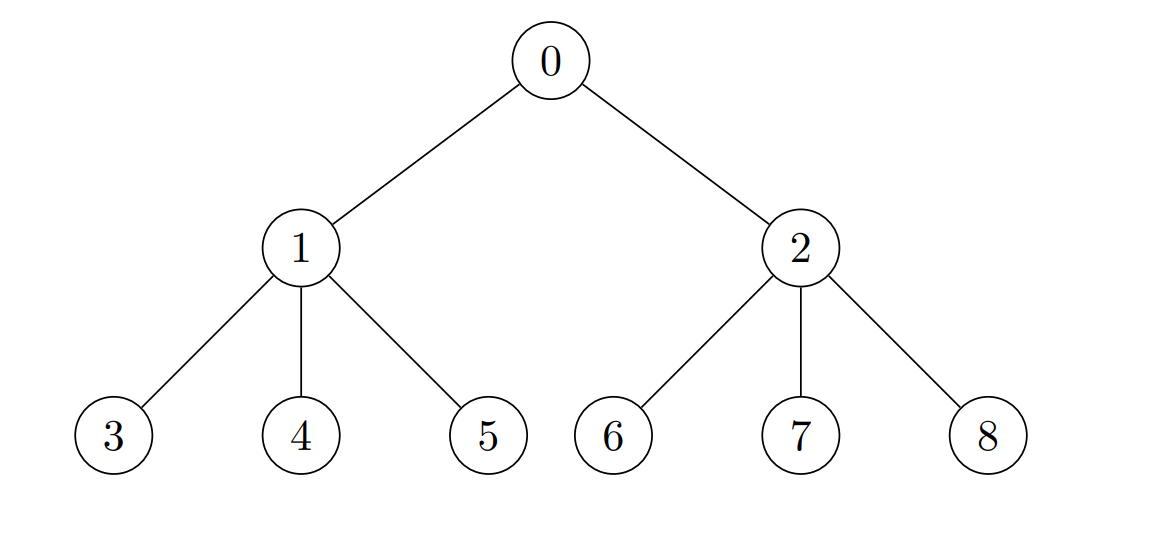
输入：edges = [[0,1],[0,2],[1,3],[1,4],[1,5],[2,6],[2,7],[2,8]], cost = [1,4,2,3,5,7,8,-4,2]
输出：[280,140,32,1,1,1,1,1,1]
解释：每个节点放置的金币数分别为：
- 节点 0 处放置 8 * 7 * 5 = 280 个金币。
- 节点 1 处放置 7 * 5 * 4 = 140 个金币。
- 节点 2 处放置 8 * 2 * 2 = 32 个金币。
- 其他节点都是叶子节点，子树内节点数目为 1 ，所以其他每个节点都放 1 个金币。

示例 3：

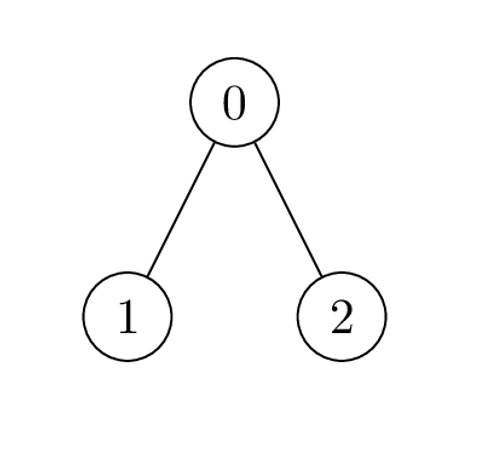
输入：edges = [[0,1],[0,2]], cost = [1,2,-2]
输出：[0,1,1]
解释：节点 1 和 2 都是叶子节点，子树内节点数目为 1 ，各放置 1 个金币。节点 0 处唯一的开销乘积是 2 * 1 * -2 = -4 。所以在节点 0 处放置 0 个金币。

提示：

• 2 <= n <= 2 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• cost.length == n
• 1 <= |cost[i]| <= 104
• edges 一定是一棵合法的树。

地址

https://leetcode.cn/contest/biweekly-contest-120/problems/find-polygon-with-the-largest-perimeter/

题意

数学问题 + 贪心

思路

1.
2. 复杂度分析：

• 时间复杂度：$O(n \log n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(n)$。

代码

class Solution:
    def largestPerimeter(self, nums: List[int]) -> int:
        n = len(nums)
        nums.sort()
        psum = [0] * (n + 1)
        for i in range(n):
            psum[i + 1] = psum[i] + nums[i]
        for i in range(n - 1, 1, -1):
            if psum[i + 1] > 2 * nums[i]:
                return psum[i + 1]
        return -1

2972. 统计移除递增子数组的数目 II

给你一个下标从 0 开始的 正 整数数组 nums 。

如果 nums 的一个子数组满足：移除这个子数组后剩余元素 严格递增 ，那么我们称这个子数组为 移除递增 子数组。比方说，[5, 3, 4, 6, 7] 中的 [3, 4] 是一个移除递增子数组，因为移除该子数组后，[5, 3, 4, 6, 7] 变为 [5, 6, 7] ，是严格递增的。

请你返回 nums 中 移除递增 子数组的总数目。

注意 ，剩余元素为空的数组也视为是递增的。

子数组 指的是一个数组中一段连续的元素序列。

示例 1：

输入：nums = [1,2,3,4]
输出：10
解释：10 个移除递增子数组分别为：[1], [2], [3], [4], [1,2], [2,3], [3,4], [1,2,3], [2,3,4] 和 [1,2,3,4]。移除任意一个子数组后，剩余元素都是递增的。注意，空数组不是移除递增子数组。

示例 2：

输入：nums = [6,5,7,8]
输出：7
解释：7 个移除递增子数组分别为：[5], [6], [5,7], [6,5], [5,7,8], [6,5,7] 和 [6,5,7,8] 。
nums 中只有这 7 个移除递增子数组。

示例 3：

输入：nums = [8,7,6,6]
输出：3
解释：3 个移除递增子数组分别为：[8,7,6], [7,6,6] 和 [8,7,6,6] 。注意 [8,7] 不是移除递增子数组因为移除 [8,7] 后 nums 变为 [6,6] ，它不是严格递增的。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-120/problems/count-the-number-of-incremovable-subarrays-ii/

题意

贪心 + 数学

思路

1. 题目比较有意思的题目，其实我们仔细分析一下，去掉一个数组中的一个连续子数组使得数组中剩余的元素严格递增，实际我们有三种去除方法：

• 去掉数组中的前 $x$ 个元素，使得剩余元素 $nums[{x+1}\cdots{n-1}]$ 严格递增；
• 去掉数组中的后 $x$ 个元素，使得剩余元素 $nums[{0}\cdots{n-x-1}]$ 严格递增；
• 去掉数组中间的 $x$ 个元素，使得剩余元素 $nums[{0}\cdots{i}]，nums[{i+x+1}\cdots{n-1}]$ 严格递增；
  根据以上分析，我们分别检测这三种情况：
• 去掉前面的元素，此时我们求出数组后部最长的严格递增的元素数组为 $nums[r\cdots{n-1}]$，此时可以构成的严格递增子数组可以为:
  $$
  nums[r\cdots n-1] \
  nums[r + 1\cdots n-1] \
  nums[r + 2\cdots n-1] \
  \cdots \
  nums[n-1] \
  $$
  一共可以有 $n-r$ 个严格递增子数组；
• 去掉后面的元素，此时我们求出数组前部最长的严格递增的元素数组为 $nums[0\cdots{l}]$，此时可以构成的严格递增子数组可以为:
  $$
  nums[0\cdots l] \
  nums[0\cdots l-1] \
  nums[0\cdots l-2] \
  \cdots \
  nums[0] \
  $$
  一共可以有 $l + 1$ 个严格递增子数组；
• 去掉中间的元素，此时假设数组的前半分数数组为 $nums[0 \cdots l]$，后半部分数组为 $nums[r \cdots n-1]$，此时需要严格保证
  • $nums[0 \cdots l]$ 严格递增；
  • $nums[r \cdots n-1]$ 严格递增；
  • $nums[r] > nums[l]$；
    实际此时我们可以用双指针，$l$ 指向数组的前半部分结尾， $r$ 指向后半部分的开头，此时移动左侧 $l$ 后，看存在多少 $r$ 满足 $nums[r] > nums[l]$;

2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 表示给定数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution:
    def incremovableSubarrayCount(self, nums: List[int]) -> int:
        n = len(nums)
        res = 1
        left, right = 1, n - 1
        while left < len(nums) and nums[left] > nums[left - 1]:
            left += 1
        while right >= 1 and nums[right - 1] < nums[right]:
            right -= 1
            
        if left == n:
            return (n  + 1) * n // 2
        else:
            l, r = left, n - right
            res += l + r
            i, j = 0, right
            while i < left:
                while j < n and nums[j] <= nums[i]:
                    j += 1
                res += n - j
                i += 1
        return res

100123. 执行操作使频率分数最大

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

你可以对数组执行 至多 k 次操作：

• 从数组中选择一个下标 i ，将 nums[i] 增加 或者 减少 1 。

最终数组的频率分数定义为数组中众数的 频率 。

请你返回你可以得到的 最大 频率分数。

众数指的是数组中出现次数最多的数。一个元素的频率指的是数组中这个元素的出现次数。

示例 1：

输入：nums = [1,2,6,4], k = 3
输出：3
解释：我们可以对数组执行以下操作：
- 选择 i = 0 ，将 nums[0] 增加 1 。得到数组 [2,2,6,4] 。
- 选择 i = 3 ，将 nums[3] 减少 1 ，得到数组 [2,2,6,3] 。
- 选择 i = 3 ，将 nums[3] 减少 1 ，得到数组 [2,2,6,2] 。
元素 2 是最终数组中的众数，出现了 3 次，所以频率分数为 3 。
3 是所有可行方案里的最大频率分数。

示例 2：

输入：nums = [1,4,4,2,4], k = 0
输出：3
解释：我们无法执行任何操作，所以得到的频率分数是原数组中众数的频率 3 。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109
• 0 <= k <= 1014

地址

https://leetcode.cn/contest/weekly-contest-376/problems/apply-operations-to-maximize-frequency-score/

题意

树上dp

思路

1. 题目首先是个比较简单的题目，不晓得为啥标记为难题，首先可以知道一点，子数中 $3$ 个不同节点的乘积的最大值可以以下两种情况构成：

• 值为整数的最大的 $3$ 个值相乘；
• 正数的最大值乘以负数最小的两个值相乘；
  由于只有上述两种情况，因此我们每次遍历时返回当前节点为根的子树中的 $5$ 个节点的值:
• 正数最大的三个值；
• 负数最大的两个值；
  然后求得当前子树需要放置的金币数目。

2. 复杂度分析:

• 时间复杂度：$O(n)$，其中 $n$ 表示树中节点的数目;
• 空间复杂度：$O(\log n)$，其中 $n$ 表示树中节点的数目;

代码

class Solution {
public:
    vector<long long> placedCoins(vector<vector<int>>& edges, vector<int>& cost) {
        int n = cost.size();
        vector<vector<int>> graph(n);
        vector<int> child(n);
        vector<long long> coins(n);
        
        for (auto v : edges) {
            graph[v[0]].emplace_back(v[1]);
            graph[v[1]].emplace_back(v[0]);
        }
        
        function<int(int, int)> dfs1 = [&](int root, int parent) {
            int res = 1;
            for (auto v : graph[root]) {
                if (v == parent) continue;
                res += dfs1(v, root);
            }
            child[root] = res;
            return res;
        };
        
        function<vector<vector<int>>(int, int)> dfs2 = [&](int root, int parent) {
            vector<int> pos(3, 0);
            vector<int> neg(3, 0);
            if (cost[root] > 0) {
                pos.emplace_back(cost[root]);
            } else {
                neg.emplace_back(cost[root]);
            }
            
            for (auto v : graph[root]) {
                if (v == parent) continue;
                auto vec = dfs2(v, root);
                pos.insert(pos.end(), vec[0].begin(), vec[0].end());
                neg.insert(neg.end(), vec[1].begin(), vec[1].end());
            }
            sort(pos.begin(), pos.end(), [](int x, int y) {
                return x > y;
            });
            sort(neg.begin(), neg.end());
            vector<vector<int>> res(2, vector<int>(3));
            for (int i = 0; i < 3; i++) {
                res[0][i] = pos[i];
                res[1][i] = neg[i];
            }
            if (child[root] < 3) {
                coins[root] = 1;
            } else {
                coins[root] = max((long long)pos[0] * pos[1] * pos[2], (long long)pos[0] * neg[0] * neg[1]);
            }
            return res;
        };
        
        dfs1(0, -1);
        dfs2(0, -1);
        return coins;
    }
};         

欢迎关注和打赏，感谢支持！

• 关注我的博客: https://mike-box.github.io/

• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu