leetcode biweekly contes 118 T4 题目太难,竟然没有想出来,前三题确实是水题。
100121. 查找包含给定字符的单词 给你一个下标从 0 开始的字符串数组 words 和一个字符 x 。
请你返回一个 下标数组 ,表示下标在数组中对应的单词包含字符 x 。
注意 ,返回的数组可以是 任意 顺序。
示例 1:
输入:words = ["leet","code"], x = "e" 输出:[0,1] 解释:"e" 在两个单词中都出现了:"leet" 和 "code" 。所以我们返回下标 0 和 1 。
示例 2:
输入:words = ["abc","bcd","aaaa","cbc"], x = "a" 输出:[0,2] 解释:"a" 在 "abc" 和 "aaaa" 中出现了,所以我们返回下标 0 和 2 。
示例 3:
输入:words = ["abc","bcd","aaaa","cbc"], x = "z" 输出:[] 解释:"z" 没有在任何单词中出现。所以我们返回空数组。
提示:
1 <= words.length <= 501 <= words[i].length <= 50x 是一个小写英文字母。words[i] 只包含小写英文字母。
地址 https://leetcode.cn/contest/biweekly-contest-118/problems/find-words-containing-character/
题意 枚举
思路
简单题目,直接枚举即可,遍历每个字符串并检测每个字符串是否含有特定字符 $c$ 即可。
复杂度分析:
时间复杂度:$O(n)$,其中 $n$ 表示给定的数组的长度。
空间复杂度:$O(1)$。
代码 class Solution : def findWordsContaining (self, words: List [str ], x: str ) -> List [int ]: return [i for i in range (len (words)) if words[i].count(x) > 0 ]
100138. 最大化网格图中正方形空洞的面积 给你一个网格图,由 n + 2 条 横线段 和 m + 2 条 竖线段 组成,一开始所有区域均为 1 x 1 的单元格。
所有线段的编号从 1 开始。
给你两个整数 n 和 m 。
同时给你两个整数数组 hBars 和 vBars 。
hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。
如果满足以下条件之一,你可以 移除 两个数组中的部分线段:
如果移除的是横线段,它必须是 hBars 中的值。
如果移除的是竖线段,它必须是 vBars 中的值。
请你返回移除一些线段后(可能不移除任何线段) ,剩余网格图中 最大正方形 空洞的面积,正方形空洞的意思是正方形 内部 不含有任何线段。
示例 1:
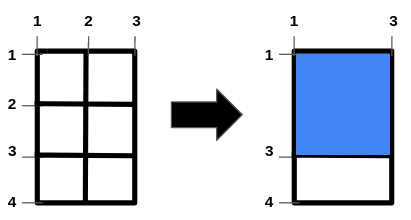
输入:n = 2, m = 1, hBars = [2,3], vBars = [2] 输出:4 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,4] ,竖线编号的范围是区间 [1,3] 。 可以移除的横线段为 [2,3] ,竖线段为 [2] 。 一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。 操作后得到的网格图如右图所示。 正方形空洞面积为 4。 无法得到面积大于 4 的正方形空洞。 所以答案为 4 。
示例 2:
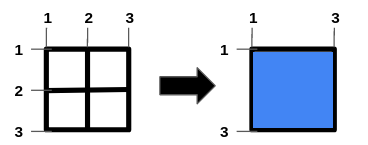
输入:n = 1, m = 1, hBars = [2], vBars = [2] 输出:4 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,3] ,竖线编号的范围是区间 [1,3] 。 可以移除的横线段为 [2] ,竖线段为 [2] 。 一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。 操作后得到的网格图如右图所示。 正方形空洞面积为 4。 无法得到面积大于 4 的正方形空洞。 所以答案为 4 。
示例 3:
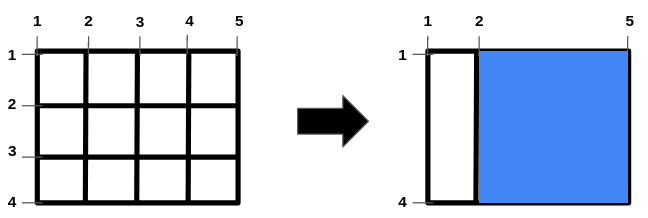
输入:n = 2, m = 3, hBars = [2,3], vBars = [2,3,4] 输出:9 解释:左边的图是一开始的网格图。 横线编号的范围是区间 [1,4] ,竖线编号的范围是区间 [1,5] 。 可以移除的横线段为 [2,3] ,竖线段为 [2,3,4] 。 一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。 操作后得到的网格图如右图所示。 正方形空洞面积为 9。 无法得到面积大于 9 的正方形空洞。 所以答案为 9 。
提示:
1 <= n <= 1091 <= m <= 1091 <= hBars.length <= 1002 <= hBars[i] <= n + 11 <= vBars.length <= 1002 <= vBars[i] <= m + 1hBars 中的值互不相同。vBars 中的值互不相同。
地址 https://leetcode.cn/contest/biweekly-contest-118/problems/maximize-area-of-square-hole-in-grid/
题意 贪心
思路
由于矩阵的横坐标与纵坐标是分开计算的,此时我们只需要分别计算出横向与纵向分别可以切出的连续最大块,并取最小值。构成的最大的正方形及横向与纵向切出来的最小值。
复杂度分析:
时间复杂度:$O(n \log n + m \log m)$,其中 $m,n$ 表示给定的数字。
空间复杂度:$O(1)$,其中 $n$ 表示给定字符串的长度。
代码 class Solution : def maximizeSquareHoleArea (self, n: int , m: int , hBars: List[int ], vBars: List[int ]) -> int : def calc(nums): res, pre = 0 , 0 cnt = 1 for x in nums: if x == pre + 1 : cnt += 1 else : cnt = 2 pre = x res = max (res, cnt) return res hBars.sort () vBars.sort () x = min (calc (hBars), calc (vBars)) return x * x
100133. 购买水果需要的最少金币数 你在一个水果超市里,货架上摆满了玲琅满目的奇珍异果。
给你一个下标从 1 开始的数组 prices ,其中 prices[i] 表示你购买第 i 个水果需要花费的金币数目。
水果超市有如下促销活动:
如果你花费 price[i] 购买了水果 i ,那么接下来的 i 个水果你都可以免费获得。
注意 ,即使你 可以 免费获得水果 j ,你仍然可以花费 prices[j] 个金币去购买它以便能免费获得接下来的 j 个水果。
请你返回获得所有水果所需要的 最少 金币数。
示例 1:
输入:prices = [3,1,2] 输出:4 解释:你可以按如下方法获得所有水果: - 花 3 个金币购买水果 1 ,然后免费获得水果 2 。 - 花 1 个金币购买水果 2 ,然后免费获得水果 3 。 - 免费获得水果 3 。 注意,虽然你可以免费获得水果 2 ,但你还是花 1 个金币去购买它,因为这样的总花费最少。 购买所有水果需要最少花费 4 个金币。
示例 2:
输入:prices = [1,10,1,1] 输出:2 解释:你可以按如下方法获得所有水果: - 花 1 个金币购买水果 1 ,然后免费获得水果 2 。 - 免费获得水果 2 。 - 花 1 个金币购买水果 3 ,然后免费获得水果 4 。 - 免费获得水果 4 。 购买所有水果需要最少花费 2 个金币。
提示:
1 <= prices.length <= 10001 <= prices[i] <= 105
地址 https://leetcode.cn/contest/weekly-contest-372/problems/maximum-xor-product/
题意
动态规划 + 滑动窗口
思路
动态规划思路比较简单,设 $dp[i]$ 表示从第 $i$ 个位置开始购买水果,且购买 $[i,n-1]$ 所有的水果需要的最少花费,此时设 $dp[i]$ ,则此时假设购买第 $i$ 个水果,此时可以拿走 $[i, i+i]$ 之间的所有水果,此时我们只需要遍历是否还可以购买 $[i+1, i + i + 1]$ 区间内的水果构成的最小值。
时间复杂度:$O(n^2)$,其中$n$ 表示给定数组的长度;
空间复杂度:$O(n)$,其中$n$ 表示给定数组的长度;
代码 class Solution {public : int minimumCoins (vector<int >& prices) int n = prices.size (); vector<int > dp (n, INT_MAX) ; priority_queue<pair<int , int >, vector<pair<int , int >>, greater<pair<int , int >>> pq; for (int i = n - 1 ; i >= 0 ; i--) { if (2 * (i + 1 ) >= n) { dp[i] = prices[i]; } else { while (!pq.empty () && pq.top ().second > 2 * i + 2 ) { pq.pop (); } dp[i] = pq.top ().first + prices[i]; } pq.emplace (dp[i], i); } return dp[0 ]; } };
class Solution : def minimumCoins (self, prices: List [int ] ) -> int : n = len (prices) dp = [inf] * n for i in range (n - 1 , -1 , -1 ): if 2 * (i + 1 ) >= n: dp[i] = prices[i] else : for j in range (i + 1 , min (n, 2 * (i + 1 ) + 1 )): dp[i] = min (dp[i], prices[i] + dp[j]) return dp[0 ]
100135. 找到最大非递减数组的长度 给你一个下标从 0 开始的整数数组 nums 。
你可以执行任意次操作。每次操作中,你需要选择一个 子数组 ,并将这个子数组用它所包含元素的 和 替换。比方说,给定数组是 [1,3,5,6] ,你可以选择子数组 [3,5] ,用子数组的和 8 替换掉子数组,然后数组会变为 [1,8,6] 。
请你返回执行任意次操作以后,可以得到的 最长非递减 数组的长度。
子数组 指的是一个数组中一段连续 非空 的元素序列。
示例 1:
输入:nums = [5,2,2] 输出:1 解释:这个长度为 3 的数组不是非递减的。 我们有 2 种方案使数组长度为 2 。 第一种,选择子数组 [2,2] ,对数组执行操作后得到 [5,4] 。 第二种,选择子数组 [5,2] ,对数组执行操作后得到 [7,2] 。 这两种方案中,数组最后都不是 非递减 的,所以不是可行的答案。 如果我们选择子数组 [5,2,2] ,并将它替换为 [9] ,数组变成非递减的。 所以答案为 1 。
示例 2:
输入:nums = [1,2,3,4] 输出:4 解释:数组已经是非递减的。所以答案为 4 。
示例 3:
输入:nums = [4,3,2,6] 输出:3 解释:将 [3,2] 替换为 [5] ,得到数组 [4,5,6] ,它是非递减的。 最大可能的答案为 3 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 105
地址 https://leetcode.cn/contest/biweekly-contest-118/problems/find-maximum-non-decreasing-array-length/
题意
单调栈 + 二分
思路
这道题目应该是最近几周遇到的最经典的题目了,还是非常难得题目,需要仔细思考。我们首先需要设几个通用变量,设 $dp[i]$ 表示前 $i$ 个元素组成的最长非递减的子数组的长度,$last[i]$ 表示前 $i$ 个元素组成最长非递减子数组时,最后一个元素的大小,此时我们可以知道几个关键点:
对于 $j < i$, 如果满足 $sum[i] - sum[j] \ge last[j]$ 时,此时子数组 $nums[i \cdots j]$ 一定可以接到前 $j$ 个元素组成的最长非递减的子数组后面,此时可以知道 $dp[i] = dp[j] + 1$, 此时 $last[i] = sum[i] - sum[j]$;
我们将上述不等式变换一下即为 $sum[i] \ge sum[j] + last[j]$, 我们可以把前 $i$ 个元素的中每个索引 $j$ 的和 $sum[j] + last[j]$ 专门用一个数组存储起来,此时我们只需要找到尽可能的大 $j$,满足 $sum[i] \ge sum[j] + last[j]$。为什么 $j$ 要尽可能的大,因此此时才能使得最后一个元素 $last[i] = sum[i] - sum[j]$ 尽可能的小,才可能使得当前数组容易向后继续扩展,最暴力的解法即使用线段树上的二分查找,尽量找到最大的索引 $j$,且满足 $sum[j] + last[j] \le sum[i]$。
知道上述变换后我们需要思考一下,对当前的 $sum[i]$ 来说,假设当前的栈中存储的序列有序,此时我们即可用二分查找找到最大的 $j$, 但实际来看对于 $sum[j] + last[j]$ 组成的序列并不是递增有序的。但为什么我们可以用单调栈保障其有序,假设满足 $sum[j] + last[j] < sum[i] + last[i], j < i$,假设存在 $j < k < i$ 时,此时满足 $sum[k] + last[k] \le sum[i] + last[i], k < i$,此时对于 $i$ 来说,由于 $dp[i] \ge dp[k]$,此时对于扩展来说我们应该有限选取最靠近 $i$ 且二者之和尽可能小的元素,因此实际在扩展过程中对于和后面元素的索引在贪心策略中可以直接不被选中。
当求出 $i$ 为结尾的最长序列时,此时我们将单调栈中的顶部所有大于等于 $sum[i] + last[i]$ 的元素可以全部从栈中移除。
复杂度分析:
时间复杂度:$O(n \log n)$,其中 $n$ 表示数组的长度;
空间复杂度:$O(n)$,其中 $n$ 表示数组的长度;
代码 class Solution : def findMaximumLength (self, nums: List [int ] ) -> int : n = len (nums) psum = [0 ] * (n + 1 ) dp = [0 ] * (n + 1 ) last = [0 ] * (n + 1 ) st = [] for i, x in enumerate (nums): psum[i + 1 ] = psum[i] + x dp[0 ] = 0 st.append([0 , 0 ]) for i in range (1 , n + 1 ): L, R = 0 , len (st) - 1 index = 0 while L <= R: mid = (L + R) // 2 if st[mid][0 ] <= psum[i]: index = st[mid][1 ] L = mid + 1 else : R = mid - 1 j = index dp[i] = dp[j] + 1 last[i] = psum[i] - psum[j] while len (st) > 0 and st[-1 ][0 ] >= psum[i] + last[i]: st.pop() st.append([psum[i] + last[i], i]) return dp[n]
class Solution {public : int findMaximumLength (vector<int >& nums) int n = nums.size (); vector<long long > sum (n + 1 ) ; vector<int > dp (n + 1 ) ; vector<long long > last (n + 1 ) ; vector<pair<long long , int >> st; for (int i = 0 ; i < n; i++) { sum[i + 1 ] = sum[i] + nums[i]; } dp[0 ] = 0 ; st.emplace_back (0 , 0 ); for (int i = 1 ; i <= n; i++) { int L = 0 , R = st.size () - 1 ; int index = 0 ; while (L <= R) { int mid = (L + R) >> 1 ; if (st[mid].first <= sum[i]) { index = st[mid].second; L = mid + 1 ; } else { R = mid - 1 ; } } int j = index; dp[i] = dp[j] + 1 ; last[i] = sum[i] - sum[j]; while (st.size () > 0 && st.back ().first >= sum[i] + last[i]) { st.pop_back (); } st.emplace_back (sum[i] + last[i], i); } return dp[n]; } };
#define CHL(x) (x * 2) #define CHR(x) (x * 2 + 1) const int MAXN = 4e5 + 7 ;struct SegTreeNode { int l, r; long long minVal; }; SegTreeNode tree[MAXN]; void pushUpTree (int idx) tree[idx].minVal = min (tree[CHL (idx)].minVal, tree[CHR (idx)].minVal); } void buildTree (int idx, int l, int r) if (l > r) { return ; } if (l == r) { tree[idx].l = tree[idx].r = l; tree[idx].minVal = LLONG_MAX; return ; } tree[idx].l = l; tree[idx].r = r; int mid = (l + r) / 2 ; buildTree (CHL (idx), l, mid); buildTree (CHR (idx), mid + 1 , r); pushUpTree (idx); } void updateTree (int x, long long val, int idx) if (x < tree[idx].l || x > tree[idx].r) { return ; } if (x == tree[idx].l && x == tree[idx].r) { tree[idx].minVal = val; return ; } int mid = (tree[idx].l + tree[idx].r) / 2 ; if (x <= mid) { updateTree (x, val, CHL (idx)); } else { updateTree (x, val, CHR (idx)); } pushUpTree (idx); } int queryTree (int l, int r, long long target, int idx) if (tree[idx].minVal > target) { return -1 ; } if (r < tree[idx].l || l > tree[idx].r) { return -1 ; } if (l == r) { return l; } int mid = (tree[idx].l + tree[idx].r) / 2 ; if (mid + 1 <= r) { int ret = queryTree (mid + 1 , r, target, CHR (idx)); if (ret >= 0 ) { return ret; } } return queryTree (l, mid, target, CHL (idx)); } class Solution {public : int findMaximumLength (vector<int >& nums) int n = nums.size (); vector<long long > sum (n + 1 ) ; vector<long long > last (n + 1 ) ; vector<int > dp (n + 1 ) ; buildTree (1 , 0 , n); for (int i = 0 ; i < n; i++) { sum[i + 1 ] = sum[i] + nums[i]; } dp[0 ] = 0 ; last[0 ] = 0 ; updateTree (0 , 0 , 1 ); for (int i = 1 ; i <= n; i++) { int j = queryTree (0 , i - 1 , sum[i], 1 ); dp[i] = dp[j] + 1 ; updateTree (i, sum[i] + sum[i] - sum[j], 1 ); } return dp[n]; } };
欢迎关注和打赏,感谢支持!