leetcode biweekly contest 119

这么快力扣都已经到了双周赛 119 了，虽然总体还不错，本周的两次周赛都是手速场，不需要太多的技巧与难度。

100130. 找到两个数组中的公共元素显示英文描述

给你两个下标从 0 开始的整数数组 nums1 和 nums2 ，它们分别含有 n 和 m 个元素。

请你计算以下两个数值：

统计 0 <= i < n 中的下标 i ，满足 nums1[i] 在 nums2 中至少出现了一次。
统计 0 <= i < m 中的下标 i ，满足 nums2[i] 在 nums1 中至少出现了一次。
请你返回一个长度为 2 的整数数组 answer ，按顺序分别为以上两个数值。

示例 1：

输入：nums1 = [4,3,2,3,1], nums2 = [2,2,5,2,3,6]
输出：[3,4]
解释：分别计算两个数值：
- nums1 中下标为 1 ，2 和 3 的元素在 nums2 中至少出现了一次，所以第一个值为 3 。
- nums2 中下标为 0 ，1 ，3 和 4 的元素在 nums1 中至少出现了一次，所以第二个值为 4 。

示例 2：

输入：nums1 = [3,4,2,3], nums2 = [1,5]
输出：[0,0]
解释：两个数组中没有公共元素，所以两个值都为 0 。

提示：

n == nums1.length
m == nums2.length
1 <= n, m <= 100
1 <= nums1[i], nums2[i] <= 100

地址

https://leetcode.cn/contest/biweekly-contest-119/problems/find-common-elements-between-two-arrays/

题意

直接模拟

思路

直接模拟即可，模拟移位即可。
复杂度分析：

时间复杂度：$O(n^2)$，其中 $n$ 表示给定的矩阵的行数。
空间复杂度：$O(1)$。

代码

class Solution:
    def findIntersectionValues(self, nums1: List[int], nums2: List[int]) -> List[int]:
        cnt1 = set(nums1)
        cnt2 = set(nums2)
        return [sum(x in cnt2 for x in nums1), sum(x in cnt1 for x in nums2)]

100152消除相邻近似相等字符

给你一个下标从 0 开始的字符串 word 。

一次操作中，你可以选择 word 中任意一个下标 i ，将 word[i] 修改成任意一个小写英文字母。

请你返回消除 word 中所有相邻 近似相等 字符的最少操作次数。

两个字符 a 和 b 如果满足 a == b 或者 a 和 b 在字母表中是相邻的，那么我们称它们是 近似相等 字符。

示例 1：

输入：word = "aaaaa"
输出：2
解释：我们将 word 变为 "acaca" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 2 次操作。

示例 2：

输入：word = "abddez"
输出：2
解释：我们将 word 变为 "ybdoez" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 2 次操作。

示例 3：

输入：word = "zyxyxyz"
输出：3
解释：我们将 word 变为 "zaxaxaz" ，该字符串没有相邻近似相等字符。
消除 word 中所有相邻近似相等字符最少需要 3 次操作

提示：

1 <= word.length <= 100
word 只包含小写英文字母。

地址

https://leetcode.cn/contest/biweekly-contest-119/problems/remove-adjacent-almost-equal-characters/

题意

贪心

思路

由于题目只需要保证相邻的两个的ascii 码的差的绝对值大于 $1$ 即可，此时我们 $s[i],s[i+1]$，我们应当优先修改 $s[i+1]$ 这个靠后的字符，因为 $s[i+1]$ 可能与 $s[i+2]$ 存在相邻字符，因此我们每次贪心的修改后一个字符，统计需要修改的数目即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示字符串的长度。
空间复杂度：$O(1)$，其中 $n$ 表示给定字符串的长度。

代码

class Solution:
    def removeAlmostEqualCharacters(self, word: str) -> int:
        res = 0
        i = 1
        while i < len(word):
            if abs(ord(word[i]) - ord(word[i - 1])) <= 1:
                res += 1
                i += 2
            else:
                i += 1
        return res

2958. 最多 K 个重复元素的最长子数组

给你一个整数数组 nums 和一个整数 k 。

一个元素 x 在数组中的频率指的是它在数组中的出现次数。

如果一个数组中所有元素的频率都 小于等于 k ，那么我们称这个数组是好数组。

请你返回 nums 中 最长好 子数组的长度。

子数组 指的是一个数组中一段连续非空的元素序列。

示例 1：

输入：nums = [1,2,3,1,2,3,1,2], k = 2
输出：6
解释：最长好子数组是 [1,2,3,1,2,3] ，值 1 ，2 和 3 在子数组中的频率都没有超过 k = 2 。[2,3,1,2,3,1] 和 [3,1,2,3,1,2] 也是好子数组。
最长好子数组的长度为 6 。

示例 2：

输入：nums = [1,2,1,2,1,2,1,2], k = 1
输出：2
解释：最长好子数组是 [1,2] ，值 1 和 2 在子数组中的频率都没有超过 k = 1 。[2,1] 也是好子数组。
最长好子数组的长度为 2 。

示例 3：

输入：nums = [5,5,5,5,5,5,5], k = 4
输出：4
解释：最长好子数组是 [5,5,5,5] ，值 5 在子数组中的频率没有超过 k = 4 。
最长好子数组的长度为 4 。

提示：

1 <= nums.length <= 105
1 <= nums[i] <= 109
1 <= k <= nums.length

地址

https://leetcode.cn/contest/biweekly-contest-119/problems/length-of-longest-subarray-with-at-most-k-frequency/

题意

双指针

思路

我们每次统计窗口内每个数字出现的次数，如果当前统计时发现窗口内存在某个数字出现的次数大于 $k$ ，则次数对窗口进行缩小，直到其中不再又数字出现的次数大于 $k$ 为止，次数统计窗口的长度。我们可以用哈希表统计每个数字出现的次数。

时间复杂度：$O(n)$，其中$n$ 表示给定数组的长度；
空间复杂度：$O(n)$，其中$n$ 表示给定数组的长度；

代码

class Solution:
    def maxSubarrayLength(self, nums: List[int], k: int) -> int:
        ans = 0
        j = 0
        cnt = Counter()
        for i, x in enumerate(nums):
            cnt[x] += 1
            while cnt[x] > k:
                cnt[nums[j]] -= 1
                j += 1
            ans = max(ans, i - j + 1)
        return ans

100140. 关闭分部的可行集合数目

一个公司在全国有 n 个分部，它们之间有的有道路连接。一开始，所有分部通过这些道路两两之间互相可以到达。

公司意识到在分部之间旅行花费了太多时间，所以它们决定关闭一些分部（也可能不关闭任何分部），同时保证剩下的分部之间两两互相可以到达且最远距离不超过 maxDistance 。

两个分部之间的距离是通过道路长度之和的 最小值 。

给你整数 n ，maxDistance 和下标从 0 开始的二维整数数组 roads ，其中 roads[i] = [ui, vi, wi] 表示一条从 ui 到 vi 长度为 wi的无向道路。

请你返回关闭分部的可行方案数目，满足每个方案里剩余分部之间的最远距离不超过 maxDistance。

注意，关闭一个分部后，与之相连的所有道路不可通行。

注意，两个分部之间可能会有多条道路。

示例 1：

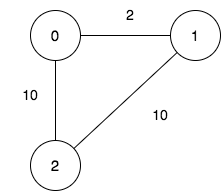
输入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
输出：5
解释：可行的关闭分部方案有：
- 关闭分部集合 [2] ，剩余分部为 [0,1] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 5 种可行的关闭方案。

示例 2：

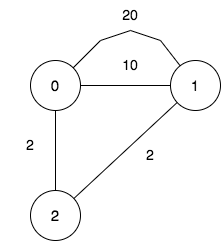
输入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
输出：7
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0,1,2] ，它们之间的最远距离为 4 。
- 关闭分部集合 [0] ，剩余分部为 [1,2] ，它们之间的距离为 2 。
- 关闭分部集合 [1] ，剩余分部为 [0,2] ，它们之间的距离为 2 。
- 关闭分部集合 [0,1] ，剩余分部为 [2] 。
- 关闭分部集合 [1,2] ，剩余分部为 [0] 。
- 关闭分部集合 [0,2] ，剩余分部为 [1] 。
- 关闭分部集合 [0,1,2] ，关闭后没有剩余分部。
总共有 7 种可行的关闭方案。

示例 3：

输入：n = 1, maxDistance = 10, roads = []
输出：2
解释：可行的关闭分部方案有：
- 关闭分部集合 [] ，剩余分部为 [0] 。
- 关闭分部集合 [0] ，关闭后没有剩余分部。
总共有 2 种可行的关闭方案。

提示：

1 <= n <= 10
1 <= maxDistance <= 105
0 <= roads.length <= 1000
roads[i].length == 3
0 <= ui, vi <= n - 1
ui != vi
1 <= wi <= 1000
一开始所有分部之间通过道路互相可以到达。

地址

https://leetcode.cn/contest/biweekly-contest-119/problems/number-of-possible-sets-of-closing-branches/

题意

二进制掩码 + Floyd算法

思路

题目由于给定的 $n$ 的数量级太小，只有 $10$, 次数我们直接暴力枚举所有可能的状态即可。枚举所有的状态，然后对所有合法的边，用 Floyd 算法求出所有不同顶点之间的最短距离，并检测是否存在两条边的长度大于 $maxDistance$ 即可。
复杂度分析:

时间复杂度：$O(n^3 \times 2^n)$，其中 $n$ 表示给定的数字；
空间复杂度：$O(n^2)$，其中 $n$ 表示给定的数字；

代码

class Solution {
public:
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
        int res = 0;
        vector<vector<int>> dist(n, vector<int>(n, INT_MAX));
        for (auto v : roads) {
            dist[v[0]][v[1]] = min(dist[v[0]][v[1]], v[2]);
            dist[v[1]][v[0]] = min(dist[v[1]][v[0]], v[2]);
        }
        for (int i = 0; i < n; i++) {
            dist[i][i] = 0;
        }
        
        for (int i = 0; i < (1 << n); i++) {
            vector<int> arr;
            for (int j = 0; j < n; j++) {
                if (i & (1 << j)) {
                    arr.emplace_back(j);
                }
            }
            
            vector<vector<int>> cost = dist;
            for (int j : arr) {
                for (int k : arr) {
                    for (int s : arr) {
                        if (cost[k][j] != INT_MAX && cost[j][s] != INT_MAX && cost[k][j] + cost[j][s] < cost[k][s]) {
                            cost[k][s] = cost[k][j] + cost[j][s];
                        }
                    }
                }
            }
            
            bool valid = true;
            for (int j : arr) {
                for (int k : arr) {
                    if (cost[k][j] > maxDistance) {
                        valid = false;
                        break;
                    }
                }
            }
            if (valid) {
                res++;
            }
        }
        return res;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 题解力扣周赛赛

← leetcode contest 375 leetcode contest 374 →

扫描二维码，分享此文章