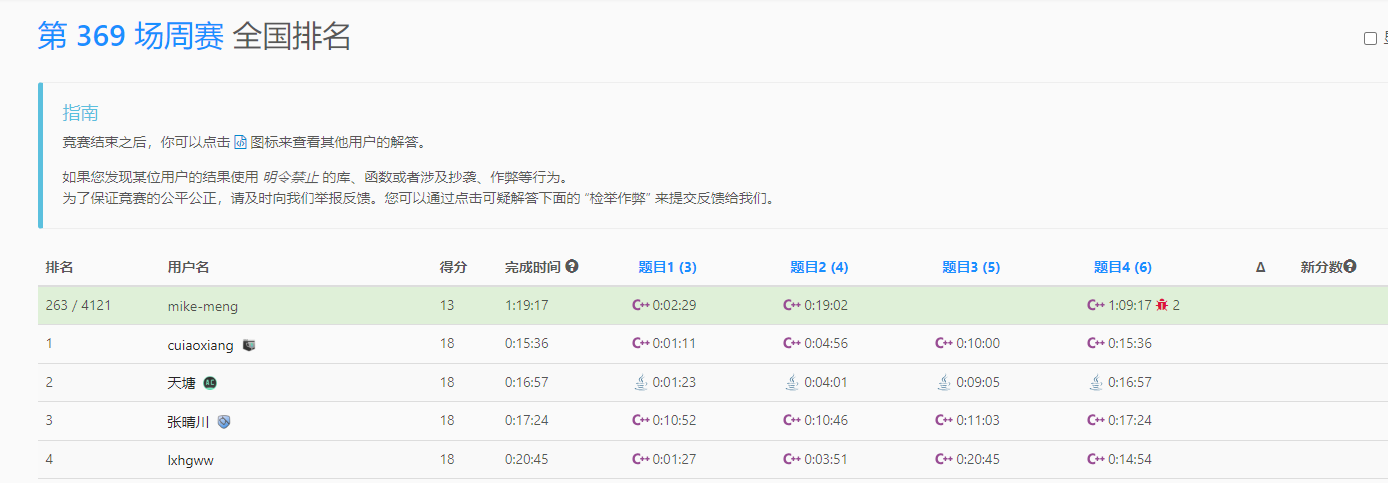
leetcode weekly contes 369

本周的题目难度还是非常高的，特别是 T3 是个好题目，容易出错，且不好写的题目，T4 倒是个简单的题目。

100111. 找出数组中的 K-or 值

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

nums 中的 K-or 是一个满足以下条件的非负整数：

只有在 nums 中，至少存在 k 个元素的第 i 位值为 1 ，那么 K-or 中的第 i 位的值才是 1 。

返回 nums 的 K-or 值。

注意：对于整数 x ，如果 (2i AND x) == 2i ，则 x 中的第 i 位值为 1 ，其中 AND 为按位与运算符。

示例 1：

输入：nums = [7,12,9,8,9,15], k = 4
输出：9
解释：nums[0]、nums[2]、nums[4] 和 nums[5] 的第 0 位的值为 1 。
nums[0] 和 nums[5] 的第 1 位的值为 1 。
nums[0]、nums[1] 和 nums[5] 的第 2 位的值为 1 。
nums[1]、nums[2]、nums[3]、nums[4] 和 nums[5] 的第 3 位的值为 1 。
只有第 0 位和第 3 位满足数组中至少存在 k 个元素在对应位上的值为 1 。因此，答案为 2^0 + 2^3 = 9 。

示例 2：

输入：nums = [2,12,1,11,4,5], k = 6
输出：0
解释：因为 k == 6 == nums.length ，所以数组的 6-or 等于其中所有元素按位与运算的结果。因此，答案为 2 AND 12 AND 1 AND 11 AND 4 AND 5 = 0 。

示例 3：

输入：nums = [10,8,5,9,11,6,8], k = 1
输出：15
解释：因为 k == 1 ，数组的 1-or 等于其中所有元素按位或运算的结果。因此，答案为 10 OR 8 OR 5 OR 9 OR 11 OR 6 OR 8 = 15 。

提示：

1 <= nums.length <= 50
0 <= nums[i] < 231
1 <= k <= nums.length

地址

https://leetcode.cn/contest/weekly-contest-369/problems/find-the-k-or-of-an-array/

题意

模拟

思路

统计数组中每个元素在某一位中出现的个数即可，python 可以一行即可完成相关计算，写起来很舒服。
复杂度分析：

时间复杂度：$O(Cn)$，其中 $n$ 表示给定的数组的长度， $C$ 在这里等于 $32$。
空间复杂度：$O(1)$。

代码

class Solution:
    def findKOr(self, nums: List[int], k: int) -> int:
        return sum(1 << i for i in range(32) if sum([1 for x in nums if (x & (1 << i)) != 0]) >= k )

100102. 数组的最小相等和

给你两个由正整数和 0 组成的数组 nums1 和 nums2 。

你必须将两个数组中的所有 0 替换为严格正整数，并且满足两个数组中所有元素的和相等。

返回最小相等和，如果无法使两数组相等，则返回 -1 。

示例 1：

输入：nums1 = [3,2,0,1,0], nums2 = [6,5,0]
输出：12
解释：可以按下述方式替换数组中的 0 ：
- 用 2 和 4 替换 nums1 中的两个 0 。得到 nums1 = [3,2,2,1,4] 。
- 用 1 替换 nums2 中的一个 0 。得到 nums2 = [6,5,1] 。
两个数组的元素和相等，都等于 12 。可以证明这是可以获得的最小相等和。

示例 2：

输入：nums1 = [2,0,2,0], nums2 = [1,4]
输出：-1
解释：无法使两个数组的和相等。

提示：

1 <= nums1.length, nums2.length <= 105
0 <= nums1[i], nums2[i] <= 106

地址

https://leetcode.cn/contest/weekly-contest-369/problems/minimum-equal-sum-of-two-arrays-after-replacing-zeros/

题意

数论

思路

题目本身不是很难，但是理由一些数学的逻辑思考在里面，还是很考验技巧。首先我们知道所有的 $0$ 都最少为 $1$，则我们将 $0$ 全部都填充上 $1$，此时我们可以知道有以下几种情况无法继续填补：
- 如果数组 $1$ 的元素和大于数组 $2$ 的元素和，且数组 $2$ 中没有 $0$ ，则此时数组 $2$ 无法继续在 $0$ 上增加，此时则返回 $-1$;
- 如果数组 $2$ 的元素和大于数组 $1$ 的元素和，且数组 $1$ 中没有 $0$ ，则此时数组 $1$ 无法继续在 $0$ 上增加，此时则返回 $-1$;
- 如果数组 $1$ 的和不等于数组 $2$ 的和，但二者均没有 $0$ 可以继续改变当前的元素，则此时返回 $-1$;
- 看了灵神的解答，还是非常清晰的思路。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示给定的数组的长度。
空间复杂度：$O(1)$。

代码

class Solution:
    def minSum(self, nums1: List[int], nums2: List[int]) -> int:
        s1 = sum(max(x, 1) for x in nums1)
        s2 = sum(max(x, 1) for x in nums2)
        zero1 = 0 in nums1
        zero2 = 0 in nums2
        if zero1 and not zero2 and s1 > s2 or \
           not zero1 and zero2 and s1 < s2 or \
           not zero1 and not zero2 and s1 != s2:
            return -1
        return max(s1, s2)

100107. 使数组变美的最小增量运算数

给你一个下标从 0 开始、长度为 n 的整数数组 nums ，和一个整数 k 。

你可以执行下述递增运算任意次（可以是 0 次）：

从范围 [0, n - 1] 中选则一个下标 i ，并将 nums[i] 的值加 1 。

如果数组中任何长度 大于或等于 3 的子数组，其最大元素都大于或等于 k ，则认为数组是一个 美丽数组 。

以整数形式返回使数组变为 美丽数组 需要执行的最小递增运算数。

子数组是数组中的一个连续非空元素序列。

示例 1：

输入：nums = [2,3,0,0,2], k = 4
输出：3
解释：可以执行下述递增运算，使 nums 变为美丽数组：
选择下标 i = 1 ，并且将 nums[1] 的值加 1 -> [2,4,0,0,2] 。
选择下标 i = 4 ，并且将 nums[4] 的值加 1 -> [2,4,0,0,3] 。
选择下标 i = 4 ，并且将 nums[4] 的值加 1 -> [2,4,0,0,4] 。
长度大于或等于 3 的子数组为 [2,4,0], [4,0,0], [0,0,4], [2,4,0,0], [4,0,0,4], [2,4,0,0,4] 。
在所有子数组中，最大元素都等于 k = 4 ，所以 nums 现在是美丽数组。
可以证明无法用少于 3 次递增运算使 nums 变为美丽数组。
因此，答案为 3 。

示例 2：

输入：nums = [0,1,3,3], k = 5
输出：2
解释：可以执行下述递增运算，使 nums 变为美丽数组：
选择下标 i = 2 ，并且将 nums[2] 的值加 1 -> [0,1,4,3] 。
选择下标 i = 2 ，并且将 nums[2] 的值加 1 -> [0,1,5,3] 。
长度大于或等于 3 的子数组为 [0,1,5]、[1,5,3]、[0,1,5,3] 。
在所有子数组中，最大元素都等于 k = 5 ，所以 nums 现在是美丽数组。
可以证明无法用少于 2 次递增运算使 nums 变为美丽数组。 
因此，答案为 2 。

示例 3：

输入：nums = [1,1,2], k = 1
输出：0
解释：在这个示例中，只有一个长度大于或等于 3 的子数组 [1,1,2] 。
其最大元素 2 已经大于 k = 1 ，所以无需执行任何增量运算。
因此，答案为 0 。

提示：

3 <= n == nums.length <= 105
0 <= nums[i] <= 109
0 <= k <= 109

地址

https://leetcode.cn/contest/weekly-contest-369/problems/minimum-increment-operations-to-make-array-beautiful/

题意

动态规划

思路

比较简单的动态规划，不过还是挺难理解的。设 $dp[i][j]$ 表示从 $i$ 开始往左侧连续存在几个数字未进行 $k$ 替换时最小运算代价，当然我们知道 $j \le 2$ 的，因为不能出现连续 $3$ 个元素均小于 $k$, 此时我们有递推关系如下：
- 如果当前计算 $dp[i][0]$ ，即此时 $nums[i]$ 一定需要通过变换变成大于等于 $k$ 的元素，需要的代价为 $cost[i]$，此时可以从 $i-1$ 开始向左观察有以下三种情况：
  - $i-1$ 左边有 $0$ 个数未进行变换，$nums[i-1]$ 大于等于 $k$, 即此时 $dp[i][0] = \min(dp[i][0],dp[i-1][0] + cost[i])$;
  - $i-1$ 左边有 $1$ 个数未进行变换，$nums[i-1]$ 未进行变换, 即此时 $dp[i][0] = \min(dp[i][0],dp[i-1][1] + cost[i])$;
  - $i-1$ 左边有 $2$ 个数未进行变换，$nums[i-1], nums[i-2]$ 未进行变换, 即此时 $dp[i][0] = \min(dp[i][0],dp[i-1][2] + cost[i])$;
- 如果当前计算 $dp[i][1]$ ，即此时 $nums[i]$ 一定不需要变换， $i-1$ 一定进行了变换，此时可以有 $dp[i][1] = dp[i-1][0]$.
- 如果当前计算 $dp[i][2]$ ，即此时 $nums[i], nums[i-1]$ 一定不需要变换， $nums[i-2]$ 一定进行了变换，此时可以有 $dp[i][2] = dp[i-1][1]$.

时间复杂度：$O(n)$，其中$n$ 表示数组的长度；
空间复杂度：$O(1)$；

代码

class Solution {
public:
    long long minIncrementOperations(vector<int>& nums, int k) {
        int n = nums.size();
        vector<long long> dp(3, 0);
        for (int i = 0; i < n; i++) {
            vector<long long> ndp(3);
            ndp[0] = min({dp[0], dp[1], dp[2]}) + max(0, k - nums[i]);
            ndp[1] = dp[0];
            ndp[2] = dp[1];
            dp = move(ndp);
        }
        return *min_element(dp.begin(), dp.end());
    }
};

class Solution {
public:
    using LL = long long;
    constexpr static LL INF = 1e18;
    long long minIncrementOperations(vector<int>& nums, int k) {
        int n = nums.size();
        vector<vector<LL>> dp(n, vector<LL>(8, INF));
        for (int j = 1; j < 8; j++) {
            dp[2][j] = 0;
            for (int i = 0; i < 3; i++) {
                if (j & (1 << i)) {
                    dp[2][j] += max(0, k - nums[i]);
                }
            }
        }
        
        for (int i = 3; i < n; i++) {
            for (int j = 1; j < 8; j++) {
                for (int pre = 1; pre < 8; pre++) {
                    long long tot = dp[i - 1][pre];
                    for (int t = 0; t < 3; t++) {
                        if ((j & (1 << t)) != 0 && (pre & (1 << (t + 1))) == 0) {
                            tot += max(0, k - nums[i - 2 + t]);
                        }
                    }
                    dp[i][j] = min(dp[i][j], tot);
                }
            }
        }
        
        long long ans = INF;
        for (int i = 1; i < 8; i++) {
            ans = min(ans, dp[n - 1][i]);
        }
        return ans;
    }
};

100108. 收集所有金币可获得的最大积分

节点 0 处现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集所有树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出：11                        
解释：
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 =  11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。

示例 2：

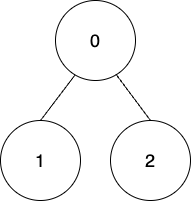
输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出：16
解释：
使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

提示：

n == coins.length
2 <= n <= 105
0 <= coins[i] <= 104
edges.length == n - 1
0 <= edges[i][0], edges[i][1] < n
0 <= k <= 104

地址

https://leetcode.cn/contest/weekly-contest-369/problems/maximum-points-after-collecting-coins-from-all-nodes/

题意

记忆化搜索

思路

题目其实不算很难，关键在于进行第一种操作时，可以使得当前元素减小一半，我们知道数组的元素的范围 $[0,10^4]$，可以知道假设对当前的根节点进行第二种方法操作缩小 $15$ 次以后，则整科树上的所有节点的值都会变为 $0$，此时我们就不需要再继续搜索了，因此每个节点的状态最多也就只有 $16$ 个，因为最多缩小 $15$ 次，设 $memo[root][x]$ 表示将当前以 $root$ 为根节点的子树缩小 $x$ 次后，该子树进行收集金币所能获得的最多得分，对于当前节点 $root$, 假设传递到它时，需要折半 $x$ 次，它有两种选择：
- 要么采用第一种方法，此时该节点收集金币的得分为 $coins[root] >> x - k$, 再加上其孩子节点折半 $x$ 次的最大得分之和；
- 要么采用第二种方法，当前节点进行折半，此时该节点收集金币的得分为 $coins[root] >> (x+1)$, 再加上其孩子节点折半 $x+1$ 次的最大得分之和；
- 通过记忆化搜索，每次记录当前节点经过折半 $x$ 次后的最大得分即可，总的来说，题目还算是比较有意思的题目，不是特别难。
复杂度分析：

时间复杂度：$O(n \log U)$，其中 $n$ 表示节点数目， $U$ 表示当前节点的金币的最大数目，最多有 $n \log U$ 个状态；
空间复杂度：$O(n\log U)$，其中 $n$ 表示节点数目， $U$ 表示当前节点的金币的最大数目；

代码

class Solution:
    def maximumPoints(self, edges: List[List[int]], coins: List[int], k: int) -> int:
        n = len(coins)
        graph = [[] for _ in range(n)]
        for x, y in edges:
            graph[x].append(y)
            graph[y].append(x)
        
        @cache
        def dfs(root, parent, cut):
            nonlocal coins
            nonlocal graph
            if cut >= 15:
                return 0
            now = coins[root] >> cut
            
            # no cut
            tot0 = now - k
            for v in graph[root]:
                if v == parent:
                    continue
                tot0 += dfs(v, root, cut)
            
            # cut one time
            tot1 = now >> 1
            for v in graph[root]:
                if v == parent:
                    continue
                tot1 += dfs(v, root, cut + 1)
            return max(tot0, tot1)
        
        return dfs(0, -1, 0)

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 题解力扣周赛赛

← leetcode biweekly contes 116 leetcode weekly contes 371 →

扫描二维码，分享此文章