leetcode biweekly contes 365
算是最近质量比较高的周赛比赛了,因为残酷刷题群的需求,以后就在美服打比赛了,国服打比赛暂时不再进行。暂时开始打比赛用C++ ,写题解用 ptyhon,感觉 python 写起来非常舒服。
2873. 有序三元组中的最大值 I
给你一个下标从 0 开始的整数数组 nums 。
请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。
下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。
示例 1:
输入:nums = [12,6,1,2,7] |
示例 2:
输入:nums = [1,10,3,4,19] |
示例 3:
输入:nums = [1,2,3] |
提示:
3 <= nums.length <= 1001 <= nums[i] <= 106
地址
https://leetcode.cn/contest/biweekly-contest-114/problems/minimum-operations-to-collect-elements/
题意
贪心策略 + 枚举
思路
- 找到最大的三元组,满足 $i < j < k$, 使得 $(nums[i] - nums[j]) * nums[k]$ 的值最大,此时我们可以枚举 $i,j,k$ 接口,此时时间复杂度为 $O(n^3)$, 当然我们还可以进一步优化,枚举中间的位置 $j$,此时只要找到 $j$ 左边的最大值 $nums[i]$,和 $j$ 右边的最大值 $k$ 即可使得上述值最大,此时枚举 $j$ 即可,同时更新 $j$ 左边与右边的最大值即可。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示数组的长度,。
- 空间复杂度:$O(1)$。
代码
class Solution: |
2874. 有序三元组中的最大值 II
给你一个下标从 0 开始的整数数组 nums 。
请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。
下标三元组 (i, j, k) 的值等于 (nums[i] - nums[j]) * nums[k] 。
示例 1:
输入:nums = [12,6,1,2,7] |
示例 2:
输入:nums = [1,10,3,4,19] |
示例 3:
输入:nums = [1,2,3] |
提示:
3 <= nums.length <= 1051 <= nums[i] <= 106
地址
https://leetcode.cn/contest/weekly-contest-365/problems/maximum-value-of-an-ordered-triplet-ii/
题意
贪心 + 枚举
思路
- 与第一题一模一样的题目,就是数量级有所变化,处理起来还是非常简单。如果还是跟第一题一样的解法,即枚举 $j$ ,且遍历时保存 $j$ 左右两遍的最大值,此时枚举 $j$ 时,当前的最大值为 $(max(nums[0,\cdots,j-1]) - nums[j]) * max(nums[j + 1, \cdots, n-1])$,我们按照上述枚举即可,我们可以通过提前计算存储所有子序列的最大值。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 为数组的长度。
代码
class Solution: |
2875. 无限数组的最短子数组
给你一个下标从 0 开始的数组 nums 和一个整数 target 。
下标从 0 开始的数组 infinite_nums 是通过无限地将 nums 的元素追加到自己之后生成的。
请你从 infinite_nums 中找出满足 元素和 等于 target 的 最短 子数组,并返回该子数组的长度。如果不存在满足条件的子数组,返回 -1 。
示例 1:
输入:nums = [1,2,3], target = 5 |
示例 2:
输入:nums = [1,1,1,2,3], target = 4 |
示例 3:
输入:nums = [2,4,6,8], target = 3 |
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1051 <= target <= 109
地址
https://leetcode.cn/contest/weekly-contest-365/problems/minimum-size-subarray-in-infinite-array/
题意
数学
思路
- 这个题目还挺有意思,其实本质还是一个思考题目,看到循环数组的样式我们就应该想到将两个重复数组合并并遍历,根据我们分析如下:
- 首先计算出数组 $nums$ 的和为 $tot$, 此时我们就需要分情况讨论:
- 如果 $target > tot$, 说明此时该数组至少会完整出现一次,此时我们只需要求数组 $nums$ 中是否存在连续子数组满足子数组的和为 $target \bmod tot$, 这就转换为了求是否存在最短的连续子数组的和等于某个特定的值,类似的题目已经出现过很多次了,可以用哈希或者双指针求即可,题目就非常简单了;假设求出最短的子数组的长度为 $l$, 则此时需要最短的长度为 $l + \lfloor\dfrac{target}{tot}\rfloor \times n$;
- 如果 $target \le tot$,此时我们只需要求数组 $nums$ 中是否存在连续子数组满足子数组的和为 $target$, 这就转换为了求是否存在最短的连续子数组的和等于某个特定的值, 找到类似的解法求出最短的长度 $l$ 即可。
- 首先计算出数组 $nums$ 的和为 $tot$, 此时我们就需要分情况讨论:
- 复杂度分析:
- 时间复杂度:$O(n)$,其中$n$ 表示数组的长度;
- 空间复杂度:$O(1)$;
代码
class Solution: |
2876. 有向图访问计数
现有一个有向图,其中包含 n 个节点,节点编号从 0 到 n - 1 。此外,该图还包含了 n 条有向边。
给你一个下标从 0 开始的数组 edges ,其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的边。
想象在图上发生以下过程:
- 你从节点
x开始,通过边访问其他节点,直到你在 此过程 中再次访问到之前已经访问过的节点。
返回数组 answer 作为答案,其中 answer[i] 表示如果从节点 i 开始执行该过程,你可以访问到的不同节点数。
示例 1:
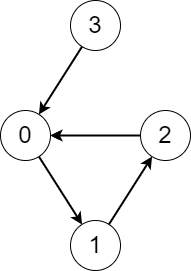
输入:edges = [1,2,0,0] |
示例 2:
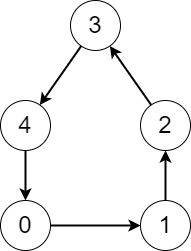
输入:edges = [1,2,3,4,0] |
提示:
n == edges.length2 <= n <= 1050 <= edges[i] <= n - 1edges[i] != i
地址
https://leetcode.cn/contest/weekly-contest-365/problems/count-visited-nodes-in-a-directed-graph/
题意
拓扑排序 + DFS
思路
- 题目为典型的 内向基环树 ,可以参考灵神的模板即可: 内向基环树处理,基本的思路是先通过拓扑排序找到不在环上的节点,剩余的节点都在环上,此时即可分开处理在环上的节点和不在环上的节点,知道上述处理思路后本题则不是特别难的题目,具体问题我们具体分析如下:
- 首先如果在环上的节点,则其从环上最多可以遍历的节点数目即等于环上节点的数目,此时非常简单,我们求出所有环的大小,并遍历换上所有的节点,此时由于从环上任意一点出发一定可以到达起点,我们直接可以求出环的大小;
- 其次如果不在环上的节点,则如何求呢,当然我们可以先求出该点到环上的距离,然后再加上环的大小即等于该节点最多可以遍历的节点数目,但是这种方法非常复杂,我们可以换种求法,我们可以从环上开始反向遍历图,此时我们反向建图即可,从图中反向开始利用
BFS或者DFS均可完成反向图的遍历。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示节点的数目;
- 空间复杂度:$O(n)$,其中 $n$ 表示节点的数目;
代码
class Solution: |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
