且听疯吟

leetcode biweekly contes 114

2023-10-05

leetcode biweekly contes 114

最近算是很水的题目了，T4 几乎是某次的原题目，确实比较简单，T3 构造题目不需要任何算法，感觉就是技巧。

8038. 收集元素的最少操作次数

给你一个正整数数组 nums 和一个整数 k 。

一次操作中，你可以将数组的最后一个元素删除，将该元素添加到一个集合中。

请你返回收集元素 1, 2, ..., k 需要的 最少操作次数 。

示例 1：

输入：nums = [3,1,5,4,2], k = 2
输出：4
解释：4 次操作后，集合中的元素依次添加了 2 ，4 ，5 和 1 。此时集合中包含元素 1 和 2 ，所以答案为 4 。

示例 2：

输入：nums = [3,1,5,4,2], k = 5
输出：5
解释：5 次操作后，集合中的元素依次添加了 2 ，4 ，5 ，1 和 3 。此时集合中包含元素 1 到 5 ，所以答案为 5 。

示例 3：

输入：nums = [3,2,5,3,1], k = 3
输出：4
解释：4 次操作后，集合中的元素依次添加了 1 ，3 ，5 和 2 。此时集合中包含元素 1 到 3  ，所以答案为 4 。

提示：

  • 1 <= nums.length <= 50
  • 1 <= nums[i] <= nums.length
  • 1 <= k <= nums.length
  • 输入保证你可以收集到元素 1, 2, ..., k 。

地址

https://leetcode.cn/contest/biweekly-contest-114/problems/minimum-operations-to-collect-elements/

题意

模拟 + 哈希

思路

  1. 直接倒序遍历，并用哈希表统计 $[1,k]$ 中出现的数字，如果全部出现则返回当前已经遍历的元素个数即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 表示数组的长度,。
  • 空间复杂度：$O(k)$，其中 $k$ 表示给定的元素,。

代码

[sol1-C++]
class Solution {
public:
    int minOperations(vector<int>& nums, int k) {
        int n = nums.size();
        unordered_set<int> cnt;
        int res = 0;
        for (int i = nums.size() - 1; i >= 0; i--) {
            if (nums[i] <= k) {
                cnt.emplace(nums[i]);
            }
            if (cnt.size() == k) {
                return n - i;
            }
        }
        return -1;
    }
};

100032. 使数组为空的最少操作次数

给你一个下标从 0 开始的正整数数组 nums 。

你可以对数组执行以下两种操作 任意次 ：

  • 从数组中选择 两个 值 相等 的元素，并将它们从数组中 删除 。
  • 从数组中选择 三个 值 相等 的元素，并将它们从数组中 删除 。

请你返回使数组为空的 最少 操作次数，如果无法达成，请返回 -1 。

示例 1：

输入：nums = [2,3,3,2,2,4,2,3,4]
输出：4
解释：我们可以执行以下操作使数组为空：
- 对下标为 0 和 3 的元素执行第一种操作，得到 nums = [3,3,2,4,2,3,4] 。
- 对下标为 2 和 4 的元素执行第一种操作，得到 nums = [3,3,4,3,4] 。
- 对下标为 0 ，1 和 3 的元素执行第二种操作，得到 nums = [4,4] 。
- 对下标为 0 和 1 的元素执行第一种操作，得到 nums = [] 。
至少需要 4 步操作使数组为空。

示例 2：

输入：nums = [2,1,2,2,3,3]
输出：-1
解释：无法使数组为空。

提示：

  • 2 <= nums.length <= 105
  • 1 <= nums[i] <= 106

地址

https://leetcode.cn/contest/biweekly-contest-114/problems/minimum-number-of-operations-to-make-array-empty/

题意

数学

思路

  1. 题目每次直接消除相同的 $2$ 或者 $3$ 个元素，因此我们可以分几种讨论：
    • 如果当前元素 $x$ 出现的次数为 $1$, 则此时无论如何都无法消除；
    • 如果当前元素 $x$ 出现的次数大于 $1$:
      • 如果当前 $x$ 出现的次数 $cnt[x]$ 刚好能被 $3$ 整除，则删除 $x$ 需要的最少此时为 $\dfrac{cnt[x]}{3}$;
      • 如果当前 $x$ 出现的次数 $cnt[x]$ 被 $3$ 整除余数为 $2$，则删除 $x$ 需要的最少此时为 $\dfrac{cnt[x] - 2}{3} + 1$, 其中有 $2$ 个元素被一起删除;
      • 如果当前 $x$ 出现的次数 $cnt[x]$ 被 $3$ 整除余数为 $1$，则删除 $x$ 需要的最少此时为 $\dfrac{cnt[x] - 4}{3} + 2$，其中有 $4$ 个元素被删除 $2$ 次；
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 为数组的长度。
  • 空间复杂度：$O(n)$，其中 $n$ 为数组的长度。

代码

class Solution {
public:
    int minOperations(vector<int>& nums) {
        int ans = 0;
        unordered_map<int, int> cnt;
        for (auto v : nums) {
            cnt[v]++;
        }
        for (auto [_, v] : cnt) {
            if (v == 1) return -1;
            if (v % 3 == 0) {
                ans += v / 3;
            } else if (v % 3 == 1) {
                ans += (v - 4) / 3 + 2;
            } else if (v % 3 == 2) {
                ans += (v - 2) / 3 + 1;
            }
        }
        return ans;
    }
};

100019. 将数组分割成最多数目的子数组

给你一个只包含 非负 整数的数组 nums 。

我们定义满足 l <= r 的子数组 nums[l..r] 的分数为 nums[l] AND nums[l + 1] AND ... AND nums[r] ，其中 AND 是按位与运算。

请你将数组分割成一个或者更多子数组，满足：

  • 每个 元素都 只 属于一个子数组。
  • 子数组分数之和尽可能 小 。

请你在满足以上要求的条件下，返回 最多 可以得到多少个子数组。

一个 子数组 是一个数组中一段连续的元素。

示例 1：

输入：nums = [1,0,2,0,1,2]
输出：3
解释：我们可以将数组分割成以下子数组：
- [1,0] 。子数组分数为 1 AND 0 = 0 。
- [2,0] 。子数组分数为 2 AND 0 = 0 。
- [1,2] 。子数组分数为 1 AND 2 = 0 。
分数之和为 0 + 0 + 0 = 0 ，是我们可以得到的最小分数之和。
在分数之和为 0 的前提下，最多可以将数组分割成 3 个子数组。所以返回 3 。

示例 2：

输入：nums = [5,7,1,3]
输出：1
解释：我们可以将数组分割成一个子数组：[5,7,1,3] ，分数为 1 ，这是可以得到的最小总分数。
在总分数为 1 的前提下，最多可以将数组分割成 1 个子数组。所以返回 1 。

提示：

  • 1 <= nums.length <= 105
  • 0 <= nums[i] <= 106

地址

https://leetcode.cn/contest/weekly-contest-364/problems/beautiful-towers-ii/

题意

贪心

思路

  1. 题目要求使得所有分组的得分之和最小，根据 与 操作的性质可以知道，所有分组之和的最小得分一定是所有元素的 AND 操作的结果，原因如下：
    • 由于 AND 的性质可以知道 $A & B \le A, A & B \le B$, 即两个数进行与操作的结果一定小于等于任何一个元素，因此我们可以知道一定是分组为 $1$ 时，所有元素进行与操作后的结果最小；
    • 需要注意的时，如果所有元素进行与操作的结果为 $0$ 时，由于 $0 + 0 = 0$ ，在这种情况下我们可以尝试将数组进行分组，使得每组元素与操作的结果都为 $0$, 因此本题目就转换成了找到连续分组元素中与操作为 $0$ 的分组数目；
    • 此时操作就比较简单了，我们只需要每次计算连续分组元素进行与操作，计算结果为 $0$ 的次数即可；
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中$n$ 表示数组的长度；
  • 空间复杂度：$O(1)$；

代码

class Solution {
public:
    int maxSubarrays(vector<int>& nums) {
        int n = nums.size();
        int tot = nums[0];
        for (auto v : nums) {
            tot = tot & v;
        }
        if (tot != 0) {
            return 1;
        }
        int ans = 0;
        int curr = 0xffffffff;
        for (int i = 0; i < n; i++) {
            curr &= nums[i];
            if (curr == 0) {
                ans++;
                curr = 0xffffffff;
            }
        }
        return ans;
    }
};

8051. 可以被 K 整除连通块的最大数目

给你一棵 n 个节点的无向树，节点编号为 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。

同时给你一个下标从 0 开始长度为 n 的整数数组 values ，其中 values[i] 是第 i 个节点的 值 。再给你一个整数 k 。

你可以从树中删除一些边，也可以一条边也不删，得到若干连通块。一个 连通块的值 定义为连通块中所有节点值之和。如果所有连通块的值都可以被 k 整除，那么我们说这是一个 合法分割 。

请你返回所有合法分割中，连通块数目的最大值 。

示例 1：

img

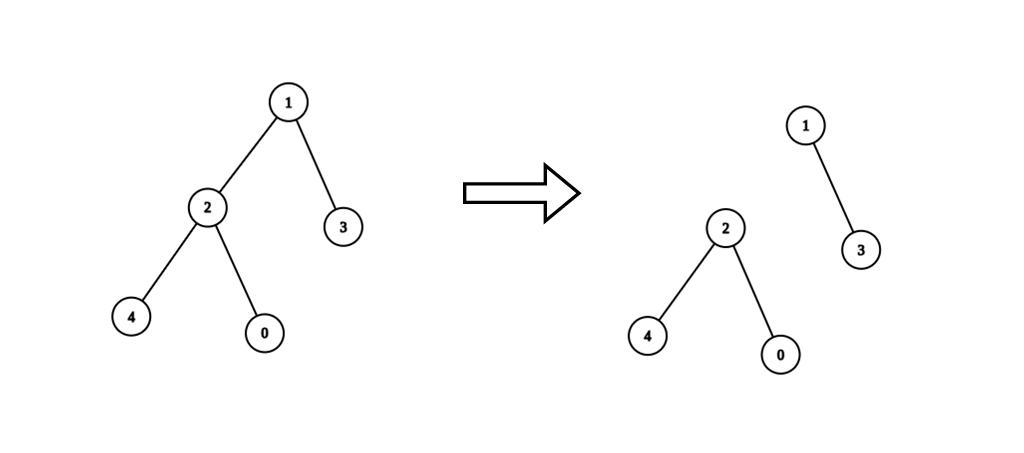
输入：n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6
输出：2
解释：我们删除节点 1 和 2 之间的边。这是一个合法分割，因为：
- 节点 1 和 3 所在连通块的值为 values[1] + values[3] = 12 。
- 节点 0 ，2 和 4 所在连通块的值为 values[0] + values[2] + values[4] = 6 。
最多可以得到 2 个连通块的合法分割。

示例 2：

img

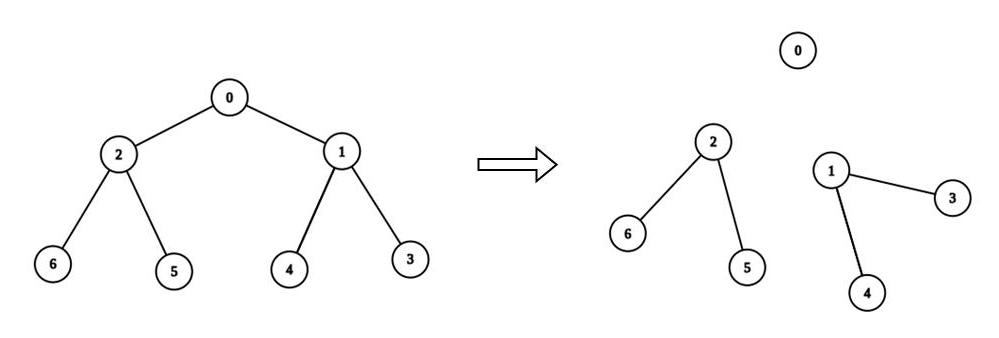
输入：n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3
输出：3
解释：我们删除节点 0 和 2 ，以及节点 0 和 1 之间的边。这是一个合法分割，因为：
- 节点 0 的连通块的值为 values[0] = 3 。
- 节点 2 ，5 和 6 所在连通块的值为 values[2] + values[5] + values[6] = 9 。
- 节点 1 ，3 和 4 的连通块的值为 values[1] + values[3] + values[4] = 6 。
最多可以得到 3 个连通块的合法分割。

提示：

  • 1 <= n <= 3 * 104
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • values.length == n
  • 0 <= values[i] <= 109
  • 1 <= k <= 109
  • values 之和可以被 k 整除。
  • 输入保证 edges 是一棵无向树。

地址

https://leetcode.cn/contest/biweekly-contest-114/problems/maximum-number-of-k-divisible-components/

题意

DFS

思路

  1. 本题与某个题目应该是一模一样的题目，感觉基本上不用思考的题目了，每次计算以当前节点为根节点且构造能被 $k$ 整除的连通单元之和被 $k$ 整除之后的余数，假设当前节点的和加上其叶子节点的分割后的剩余的返回值之和，如果构成的连通单元可以被 $k$ 整除则计算加 $1$, 否则返回被 $k$ 整除后的余数；
  2. 复杂度分析：
  • 时间复杂度：$O(E + V)$，其中 $V$ 表示树中节点的数目， $E$ 表示树中边的数目。
  • 空间复杂度：$O(E + V)$，其中 $V$ 表示树中节点的数目， $E$ 表示树中边的数目。

代码

class Solution {
public:
    int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
        vector<vector<int>> graph(n);
        long long tot = accumulate(values.begin(), values.end(), 0LL);
        for (auto e : edges) {
            graph[e[0]].emplace_back(e[1]);
            graph[e[1]].emplace_back(e[0]);
        }
        
        int res = 0;
        function<int(int, int)> dfs = [&](int root, int parent)-> int {
            long long sum = values[root];
            for (auto v : graph[root]) {
                if (v == parent) continue;
                int curr = dfs(v, root);
                sum += curr;
            }
            if (sum % k == 0) {
                res++;
            } 
            return sum % k;
        };
        dfs(0, -1);
        return res;
    }
};

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode biweekly contes 364 leetcode weekly contes 365 →

扫描二维码，分享此文章