leetcode biweekly contes 113
这次的双周赛题目还算不错,确实不太难的题目,比拼的还是手速场。
8039. 使数组成为递增数组的最少右移次数
给你一个长度为 n 下标从 0 开始的数组 nums ,数组中的元素为 互不相同 的正整数。请你返回让 nums 成为递增数组的 最少右移 次数,如果无法得到递增数组,返回 -1 。
一次 右移 指的是同时对所有下标进行操作,将下标为 i 的元素移动到下标 (i + 1) % n 处。
示例 1:
输入:nums = [3,4,5,1,2] |
示例 2:
输入:nums = [1,3,5] |
示例 3:
输入:nums = [2,1,4] |
提示:
1 <= nums.length <= 1001 <= nums[i] <= 100nums中的整数互不相同。
地址
https://leetcode.cn/contest/weekly-contest-363/problems/sum-of-values-at-indices-with-k-set-bits/
题意
直接模拟
思路
- 检测数组是否为循环递增数组,假设数组的长度为 $n$,即找到是否存在索引 $i$ 满足:
- $[0,i-1]$ 之间数组为递增,$[i,n-1]$ 之间数组递增,且满足 $nums[n-1] < nums[0]$;
- 是否满足将数组 $nums$ 循环移动 $x$ 位置后数组变为递增;
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(1)$。
代码
class Solution { |
2856. 删除数对后的最小数组长度
给你一个下标从 0 开始的 非递减 整数数组 nums 。
你可以执行以下操作任意次:
- 选择 两个 下标
i和j,满足i < j且nums[i] < nums[j]。 - 将
nums中下标在i和j处的元素删除。剩余元素按照原来的顺序组成新的数组,下标也重新从 0 开始编号。
请你返回一个整数,表示执行以上操作任意次后(可以执行 0 次),nums 数组的 最小 数组长度。
示例 1:
输入:nums = [1,3,4,9] |
示例 2:
输入:nums = [2,3,6,9] |
示例 3:
输入:nums = [1,1,2] |
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109nums是 非递减 数组。
地址
https://leetcode.cn/contest/biweekly-contest-113/problems/minimum-array-length-after-pair-removals/
题意
数学题目
思路
- 最简单的做法每次选取频次最高的两个数进行配对,最后知道剩下的即可,另一种数学方法,假设当前数组的长度为 $n$,此时出现次数最多的元素为 $nums[i]$, 出现的次数为 $x$,
- 如果 $2x > n$, 即 $x$ 出现的次数超过数组的长度的一半,此时超出 $n -x$ 的部分无法配对,此时可以配对的次数为 $n - x$ 次, 剩余 $n - 2(n-x) = 2x - n$;
- 如果 $2x \le n$:
- 如果 $n$ 为偶数则一定可以完成配对;
- 如果 $n$ 为奇数则一定存在一个元素无法完成配对;
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 为数组的长度。
代码
class Solution { |
6988. 统计距离为 k 的点对
给你一个 二维 整数数组 coordinates 和一个整数 k ,其中 coordinates[i] = [xi, yi] 是第 i 个点在二维平面里的坐标。
我们定义两个点 (x1, y1) 和 (x2, y2) 的 距离 为 (x1 XOR x2) + (y1 XOR y2) ,XOR 指的是按位异或运算。
请你返回满足 i < j 且点 i 和点 j之间距离为 k 的点对数目。
示例 1:
输入:coordinates = [[1,2],[4,2],[1,3],[5,2]], k = 5 |
示例 2:
输入:coordinates = [[1,3],[1,3],[1,3],[1,3],[1,3]], k = 0 |
提示:
2 <= coordinates.length <= 500000 <= xi, yi <= 1060 <= k <= 100
地址
https://leetcode.cn/contest/biweekly-contest-113/problems/count-pairs-of-points-with-distance-k/
题意
枚举
思路
题目初看起来貌似很难,但是关键在于 $k \in[0,100]$, $k$ 的取值范围非常小,所以导致题目就不是很难了。根据公式可以知道:
$$k = a \oplus x + b \oplus y$$,当然我们直接求 $a,b$ 比较困难,但是我们知道 $k= 100$,则此时假设 $a\oplus x = c$,则 $b \oplus y = 100 -c$,由于 $k$ 的范围非常小我们直接枚举 $c$ 的取值,则此时 $a = c \oplus x, b = y \oplus (100 - c)$, 此时我们即可知道另一个点的取值,此时我们利用哈希统计当前值为 $(a,b)$ 的点的数量,依次统计即可。
复杂度分析:
- 时间复杂度:$O(nk)$,其中 $n$ 表示数组的长度,$k$ 表示给定的元素;
- 空间复杂度:$O(n)$,其中 $n$ 表示数组的长度;
代码
class Solution { |
100041. 可以到达每一个节点的最少边反转次数
给你一个 n 个点的 简单有向图 (没有重复边的有向图),节点编号为 0 到 n - 1 。如果这些边是双向边,那么这个图形成一棵 树 。
给你一个整数 n 和一个 二维 整数数组 edges ,其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条 有向边 。
边反转 指的是将一条边的方向反转,也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。
对于范围 [0, n - 1] 中的每一个节点 i ,你的任务是分别 独立 计算 最少 需要多少次 边反转 ,从节点 i 出发经过 一系列有向边 ,可以到达所有的节点。
请你返回一个长度为 n 的整数数组 answer ,其中 answer[i]表示从节点 i 出发,可以到达所有节点的 最少边反转 次数。
示例 1:
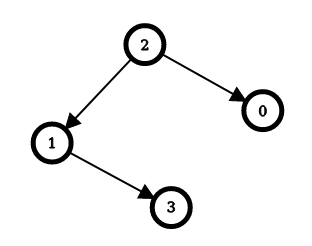
输入:n = 4, edges = [[2,0],[2,1],[1,3]] |
示例 2:
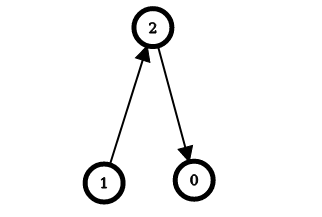
输入:n = 3, edges = [[1,2],[2,0]] |
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ui == edges[i][0] < n0 <= vi == edges[i][1] < nui != vi- 输入保证如果边是双向边,可以得到一棵树。
地址
题意
换根 dp
思路
题目还是经典的题目变形,跟「834. 树中距离之和」基本类似的题目,
首先我们统计以 $0$ 点为根时需要反转的次数,这个就用简单的 $dfs$ 即可,即统计当前从孩子节点指向父亲节点的边的数目,总的数目为 $tot$;
其次我们从 $0$ 点开始依次遍历每个节点 $x$,此时我们只需要反装从 $0$ 到 $x$ 这条路径上的边即可,其余的边保证不再反转即可,
- 此时如果当前的边是孩子节点指向父亲节点的边,则此时反转的边的数目减 $1$, 即 $tot-1$;
- 此时如果当前的边是父亲节点指向孩子节点的边,则此时反转的边的数目加 $1$, 即 $tot+1$;
复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示节点的数目。
- 空间复杂度:$O(n)$,其中 $n$ 表示节点的数目。
代码
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
