leetcode biweekly contes 110
$T4$ 应该是最近几次周赛最难的难度了,通过率创新低。
6990. 取整购买后的账户余额
一开始,你的银行账户里有 100 块钱。
给你一个整数purchaseAmount ,它表示你在一次购买中愿意支出的金额。
在一个商店里,你进行一次购买,实际支出的金额会向 最近 的 10 的 倍数 取整。换句话说,你实际会支付一个 非负 金额 roundedAmount ,满足 roundedAmount 是 10 的倍数且 abs(roundedAmount - purchaseAmount) 的值 最小 。
如果存在多于一个最接近的 10 的倍数,较大的倍数 是你的实际支出金额。
请你返回一个整数,表示你在愿意支出金额为 purchaseAmount 块钱的前提下,购买之后剩下的余额。
注意: 0 也是 10 的倍数。
示例 1:
输入:purchaseAmount = 9 |
示例 2:
输入:purchaseAmount = 15 |
提示:
0 <= purchaseAmount <= 100
地址
https://leetcode.cn/contest/biweekly-contest-110/problems/account-balance-after-rounded-purchase/
题意
直接模拟
思路
- 主要是个位数上的数字,如果个数数字小于 $5$ 则取较低下届,如果个数数字大于等于 $5$ 则取上届。
- 复杂度分析:
- 时间复杂度:$O(1)$。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6940. 在链表中插入最大公约数
给你一个链表的头 head ,每个结点包含一个整数值。
在相邻结点之间,请你插入一个新的结点,结点值为这两个相邻结点值的 最大公约数 。
请你返回插入之后的链表。
两个数的 最大公约数 是可以被两个数字整除的最大正整数。
示例 1:
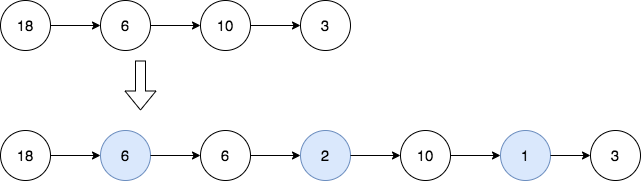
输入:head = [18,6,10,3] |
示例 2:
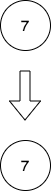
输入:head = [7] |
提示:
- 链表中结点数目在
[1, 5000]之间。 1 <= Node.val <= 1000
地址
题意
直接模拟
思路
题目本身比较简单,直接模拟即可,依次在相邻的两个节点之间插入他们的最大公约数即可。
复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为链表的长度。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6956. 使循环数组所有元素相等的最少秒数
给你一个下标从 0 开始长度为 n 的数组 nums 。
每一秒,你可以对数组执行以下操作:
- 对于范围在
[0, n - 1]内的每一个下标i,将nums[i]替换成nums[i],nums[(i - 1 + n) % n]或者nums[(i + 1) % n]三者之一。
注意,所有元素会被同时替换。
请你返回将数组 nums 中所有元素变成相等元素所需要的 最少 秒数。
示例 1:
输入:nums = [1,2,1,2] |
示例 2:
输入:nums = [2,1,3,3,2] |
示例 3:
输入:nums = [5,5,5,5] |
提示:
1 <= n == nums.length <= 1051 <= nums[i] <= 109
地址
https://leetcode.cn/contest/weekly-contest-356/problems/shortest-string-that-contains-three-strings/
题意
枚举
思路
- 非常好的题目,虽然不是很难,但是还是挺有思考的味道在里面,适合做面试。首先思考一个问题,对于数组中的每个元素,假设需要将元素 $nums[i]$ 变为目标值 $x$ ,最少需要多少次操作:
- 由于题目中可以看到,一次变换时会将 $nums[i]$ 的前后相邻的元素变为 $nums[i]$,即可将 $[i-1,i,i+1]$ 范围内的元素全部变为 $nums[i]$;
- 两次操作时,可以将 $[i-2,i-1,i,i+1,i+2]$ 等元素进行替换,此时假设元素 $nums[j]$ 距离最近的 $nums[i]$ 的循环距离为 $\min(|i-j|, n - |i - j|)$,此时我们只需要找距离 $nums[i]$ 的最小距离即可;
- 我们可以知道假设 $x$ 在数组中出现的位置从小到大为 $(d_0,d_1, \cdots,d_k)$, 则将数组中的所有元素变为 $x$ 的最大操作次数取决于 $\frac{|d_i - d_{i+1}|}{2}$ 的最大值,这是因为每个元素在变换时的最小操作数取决于它与目标值 $x$ 的最小距离;
- 由于数组为循环数组,因此我们还需要再末尾添加一个循环的索引位置 $d_0 + n$, 即此时依次相邻的位置为 $(d_0,d_1, \cdots,d_k,d_0 + n)$, 我们依次枚举数组中的每个元素,并计算将数组中的所有元素变换为当前元素的最小操作步数即可。我们可以用哈希存储每个元素出现的索引位置,然后依次计算相邻索引之间的最大距离。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示给定数组的数目。
- 空间复杂度:$O(n)$,其中 $n$ 表示给定数组的数目。
代码
class Solution { |
6987. 使数组和小于等于 x 的最少时间
给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 <= i < nums1.length ,nums1[i] 的值都增加 nums2[i] 。操作 完成后 ,你可以进行如下操作:
- 选择任一满足
0 <= i < nums1.length的下标i,并使nums1[i] = 0。
同时给你一个整数 x 。
请你返回使 nums1 中所有元素之和 小于等于 x 所需要的 最少 时间,如果无法实现,那么返回 -1 。
示例 1:
输入:nums1 = [1,2,3], nums2 = [1,2,3], x = 4 |
示例 2:
输入:nums1 = [1,2,3], nums2 = [3,3,3], x = 4 |
提示:
1 <= nums1.length <= 1031 <= nums1[i] <= 1030 <= nums2[i] <= 103nums1.length == nums2.length0 <= x <= 106
地址
https://leetcode.cn/contest/biweekly-contest-110/problems/minimum-time-to-make-array-sum-at-most-x/
题意
动态规划 + 构造
思路
- 题目还是非常难的题目,首先我们需要思考一个问题,数组需要经过多少次操作一定可以找到最小值:
- 经过仔细分析一下,我们发现 $nums_1$ 中的每个元素实际只需要一次操作,为什么只需要一次操作即可,因为每个元素操作两次会出现多余。我们可以假设 $nums1[i]$ 分别在第 $j$ 秒与第 $k$ 秒进行了两次操作,假设 $j < k$ ,即都进行了操作使得 $nums1[i] = 0$, 实际思考发现我们不需要进行第 $j$ 秒的操作,只需要进行较晚的哪一次操作第 $k$ 秒即可,此时对于数组 $nums1$ 的和不会有任何影响,即 $sum(nums1) = sum(nums1^{‘})$。
- 根据以上分析,假设数组的长度为 $n$ ,则此时我们可以想到数组一定会在 $n$ 秒内出现最小值,此时我们依次从 $1$ 到 $n$ 枚举即可,比赛的时候想到了这一步枚举,但是确实没有想到如何计算最小值。
- 如何计算上述的最小值,这就需要用到动态规划。假设我们进行了 $m$ 次操作,操作的位置分别为 $p_1,p_2,p_3, \cdots,p_m$,由于每个元素只会被操作依一次,则这些位置均不相等,此时我们可以知道:
- 第一次操作时 $nums_1[p1] + nums_2[p1]$ 变为了 $0$, 此时数组的总和减少了 $nums_1[p1] + nums_2[p1]$ ;
- 第二次操作时 $nums_1[p_2] + 2nums_2[p_2]$ 变为了 $0$, 此时数组的总和减少了 $nums_1[p_2] + 2nums_2[p_2]$ ;
- 第三次操作时 $nums_1[p_3] + 3nums_2[p_3]$ 变为了 $0$, 此时数组的总和减少了 $nums_1[p_3] + 3nums_2[p_3]$ ;
- 以上的总减少数量为即为 $sum_{i=1}^{m}(nums1[p_i] + i * nums2[p_i])$, 我们的目标是让以上减少的 $sum$ 尽可能的大;
- 根据 $1$ 的分析,我们采用动态规划找到最大的 $sum$ 即可,假设最终目标是要对操作的位置分别为 $p_1,p_2,p_3, \cdots,p_m$,那么可以确定的一定要会减少$sum_1 = \sum_{i=1}^{m}nums1[p_i]$,无论按照何种顺序操作 $sum_1$ 部分始终保持不变,剩余需要减少的部分为 $sum2 = sum_{i=1}^{m}i * nums2[p_i]$,经过分析可以知道此时一定是将最大的 $i$ 分配给最大的 $nums_2[p_i]$,因此按照 $num_2$ 的降序升序列才会使得 $sum_2$ 部分最大。
- 设 $dp[i][j]$ 表示前 $i$ 个元素中经过 $j$ 秒,此时需要选 $j$ 个元素进行操作时的最大值,则此时根据递推关系可以知道一共有两种选择:
- 对于第 $j$ 个元素选择不操作,即前 $i-1$ 个元素已经选择了 $j$ 个元素操作, 此时最大值为 $dp[i-1][j]$;
- 对于第 $j$ 个元素选择操作,此时操后后最大值增加了 $nums1[i] + j \times nums2[i]$,此时的最大值为 $dp[i][j - 1] + nums1[i] + j \times nums2[i]$;
- 增上所述可以得到 $dp[i][j] = \max(dp[i-1][j], dp[i][j -1] + nums1[i] + j \times nums2[i])$;
- 根据以上动态规划,我们可以得到前 $n$ 个元素经过 $j$ 秒后可以得到的最小值,此时即为 $sum(num1) + j \times sum(num2) - dp[n][j]$,我们依次检测最小值即可。
- 复杂度分析:
- 时间复杂度:$O(n^2)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(n^2)$,其中 $n$ 表示数组的长度。
代码
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
