且听疯吟

leetcode weekly contes 351

2023-06-26

leetcode weekly contes 351

第二题时个比较好的题目，其余的题目太一般，第二题确实是比较好的题目，也非常有难度，其余的题目太一般。

6466. 美丽下标对的数目

给你一个下标从 0 开始的整数数组 nums 。如果下标对 i、j 满足 0 ≤ i < j < nums.length ，如果 nums[i] 的 第一个数字 和 nums[j] 的 最后一个数字 互质 ，则认为 nums[i] 和 nums[j] 是一组 美丽下标对 。

返回 nums 中 美丽下标对 的总数目。

对于两个整数 x 和 y ，如果不存在大于 1 的整数可以整除它们，则认为 x 和 y 互质 。换而言之，如果 gcd(x, y) == 1 ，则认为 x 和 y 互质，其中 gcd(x, y) 是 x 和 k 最大公因数 。

示例 1：

输入：nums = [2,5,1,4]
输出：5
解释：nums 中共有 5 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 5 。2 和 5 互质，因此 gcd(2,5) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 2 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(2,1) == 1 。
i = 1 和 j = 2 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 1 。2 和 5 互质，因此 gcd(5,1) == 1 。
i = 1 和 j = 3 ：nums[0] 的第一个数字是 5 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(5,4) == 1 。
i = 2 和 j = 3 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 4 。2 和 5 互质，因此 gcd(1,4) == 1 。
因此，返回 5 。

示例 2：

输入：nums = [11,21,12]
输出：2
解释：共有 2 组美丽下标对：
i = 0 和 j = 1 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 1 。gcd(1,1) == 1 。
i = 0 和 j = 2 ：nums[0] 的第一个数字是 1 ，nums[1] 的最后一个数字是 2 。gcd(1,2) == 1 。
因此，返回 2 。

提示：

  • 2 <= nums.length <= 100
  • 1 <= nums[i] <= 9999
  • nums[i] % 10 != 0

地址

https://leetcode.cn/contest/weekly-contest-351/problems/number-of-beautiful-pairs/

题意

直接模拟

思路

  1. 找到 $(i,j)$, 检测 $nums[i]$ 的第一个数字是否与 $nums[j]$ 的最后一个数字相等即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 表示数组的长度。
  • 空间复杂度：$O(\log U)$，其中 $U$ 表示数组中的最大元素。

代码

class Solution {
public:
    int countBeautifulPairs(vector<int>& nums) {
        int n = nums.size();
        int res = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                string s1 = to_string(nums[i]);
                string s2 = to_string(nums[j]);
                int x = s1.front() - '0';
                int y = s2.back() - '0';
                if (__gcd(x, y) == 1) {
                    res++;
                }
            }
        }
        return res;
    }
};

6471. 得到整数零需要执行的最少操作数

给你两个整数：num1 和 num2 。

在一步操作中，你需要从范围 [0, 60] 中选出一个整数 i ，并从 num1 减去 2i + num2 。

请你计算，要想使 num1 等于 0 需要执行的最少操作数，并以整数形式返回。

如果无法使 num1 等于 0 ，返回 -1 。

示例 1：

输入：num1 = 3, num2 = -2
输出：3
解释：可以执行下述步骤使 3 等于 0 ：
- 选择 i = 2 ，并从 3 减去 22 + (-2) ，num1 = 3 - (4 + (-2)) = 1 。
- 选择 i = 2 ，并从 1 减去 22 + (-2) ，num1 = 1 - (4 + (-2)) = -1 。
- 选择 i = 0 ，并从 -1 减去 20 + (-2) ，num1 = (-1) - (1 + (-2)) = 0 。
可以证明 3 是需要执行的最少操作数。

示例 2：

输入：num1 = 5, num2 = 7
输出：-1
解释：可以证明，执行操作无法使 5 等于 0 。

提示：

  • 1 <= num1 <= 109
  • -109 <= num2 <= 109

地址

https://leetcode.cn/contest/weekly-contest-351/problems/minimum-operations-to-make-the-integer-zero/

题意

数学问题

思路

  1. 先思考一下，对于一个数来 $x$ 说，假设 $x$ 的数位上的 $1$ 的数目为 $n$ 最少可以分解为 $2^i$ 的和，最少需要 $x$ 次操作，假设当前的最小操作次数为 $k$，需要进行累加的数为 $t = num1 - k * num2$
  • $t \ge k$，因为此时 $t$ 最多可以被分为 $t$ 个 $1$，因此一定要满足 $num1 - k * num2 \ge k$，否则不可再分；
  • $ k \ge bitcount(t)$，因此此时 $t$ 最少能被分解为幂次和的最小此次数为 $bitcount(t)$，如果 $k < bitcount(t)$，则分解一定不能成立；
  • 满足上述两个条件下则一定成立，由于 $bitcount(t)$ 的最大值为 $40$，所以我们可以依次从最小到最大尝试即可，我们可以知道 $k$ 的上限制

  1. 根据等式 $t = num1 - k * num2$ 可以知道，$k$ 一定存在上限的，即在小于等于 $60$ 的范围内，一定可以出现匹配的 $k$；

    • $bitcount(t) \le k \le num1 - k * num2$;

  2. 复杂度分析：

  • 时间复杂度：$O(\log (num1 - num2))$。
  • 空间复杂度：$O(1)$。

代码

class Solution {
public:
    int makeTheIntegerZero(int num1, int num2) {
        if (num2 >= num1) return -1;
        for (int i = 1; i <= 60; i++) {
            long long x = (long long)num1 - (long long)i * num2;
            if (x <= 0) {
                break;
            }
            if (x >= i && __builtin_popcountll(x) <= i) {
                return i;
            }
        }
        return -1;
    }
};

2750. 将数组划分成若干好子数组的方式

给你一个二元数组 nums 。

如果数组中的某个子数组 恰好 只存在 一 个值为 1 的元素，则认为该子数组是一个 好子数组 。

请你统计将数组 nums 划分成若干 好子数组 的方法数，并以整数形式返回。由于数字可能很大，返回其对 109 + 7 取余 之后的结果。

子数组是数组中的一个连续 非空 元素序列。

示例 1：

输入：nums = [0,1,0,0,1]
输出：3
解释：存在 3 种可以将 nums 划分成若干好子数组的方式：
- [0,1] [0,0,1]
- [0,1,0] [0,1]
- [0,1,0,0] [1]

示例 2：

输入：nums = [0,1,0]
输出：1
解释：存在 1 种可以将 nums 划分成若干好子数组的方式：
- [0,1,0]

提示：

  • 1 <= nums.length <= 105
  • 0 <= nums[i] <= 1

地址

https://leetcode.cn/contest/weekly-contest-351/problems/ways-to-split-array-into-good-subarrays/

题意

组合数组

思路

  1. 感觉就是组合数学，假设一共有 $x$ 个 $1$ ，任意两个 $1$ 之间可以放置隔板的方法数为相邻的两个 $1$ 之间的距离之差，我们依次统计相邻的两个$1$ 之间的距离之差，然后求 $\prod$ 即可。

  2. 复杂度分析：

  • 时间复杂度：$O(n)$，其中 $n$ 为给定字符串的大小；
  • 空间复杂度：$O(1)$；

代码

class Solution {
public:
    int numberOfGoodSubarraySplits(vector<int>& nums) {
        int n = nums.size();
        long long mod = 1e9 + 7;
        int pre = -1;
        long long res = 1;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                if (pre >= 0) {
                    res = res * (i - pre) % mod;
                }
                pre = i;
            }
        }
        if (pre < 0) {
            return 0;
        } 
        return res;
    }
};

2751. 机器人碰撞

现有 n 个机器人，编号从 1 开始，每个机器人包含在路线上的位置、健康度和移动方向。

给你下标从 0 开始的两个整数数组 positions、healths 和一个字符串 directions（directions[i] 为 ‘L’ 表示 向左 或 ‘R’ 表示 向右）。 positions 中的所有整数 互不相同 。

所有机器人以 相同速度 同时 沿给定方向在路线上移动。如果两个机器人移动到相同位置，则会发生 碰撞 。

如果两个机器人发生碰撞，则将 健康度较低 的机器人从路线中 移除 ，并且另一个机器人的健康度 减少 1 。幸存下来的机器人将会继续沿着与之前 相同 的方向前进。如果两个机器人的健康度相同，则将二者都从路线中移除。

请你确定全部碰撞后幸存下的所有机器人的 健康度 ，并按照原来机器人编号的顺序排列。即机器人 1 （如果幸存）的最终健康度，机器人 2 （如果幸存）的最终健康度等。 如果不存在幸存的机器人，则返回空数组。

在不再发生任何碰撞后，请你以数组形式，返回所有剩余机器人的健康度（按机器人输入中的编号顺序）。

注意：位置 positions 可能是乱序的。

示例 1：

img

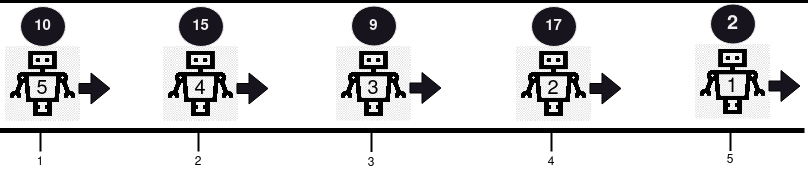
输入：positions = [5,4,3,2,1], healths = [2,17,9,15,10], directions = "RRRRR"
输出：[2,17,9,15,10]
解释：在本例中不存在碰撞，因为所有机器人向同一方向移动。所以，从第一个机器人开始依序返回健康度，[2, 17, 9, 15, 10] 。

示例 2：

img

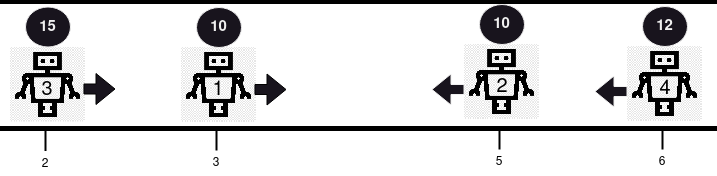
输入：positions = [3,5,2,6], healths = [10,10,15,12], directions = "RLRL"
输出：[14]
解释：本例中发生 2 次碰撞。首先，机器人 1 和机器人 2 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。接下来，机器人 3 和机器人 4 将会发生碰撞，由于机器人 4 的健康度更小，则它会被移除，而机器人 3 的健康度变为 15 - 1 = 14 。仅剩机器人 3 ，所以返回 [14] 。

示例 3：

img

输入：positions = [1,2,5,6], healths = [10,10,11,11], directions = "RLRL"
输出：[]
解释：机器人 1 和机器人 2 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。机器人 3 和机器人 4 将会碰撞，因为二者健康度相同，二者都将被从路线中移除。所以返回空数组 [] 。

提示：

  • 1 <= positions.length == healths.length == directions.length == n <= 105
  • 1 <= positions[i], healths[i] <= 109
  • directions[i] == 'L' 或 directions[i] == 'R'
  • positions 中的所有值互不相同

地址

https://leetcode.cn/contest/weekly-contest-351/problems/robot-collisions/

题意

栈 + 模拟

思路

  1. 比较简单的题目，首先我们应该将所有的机器人按照位置进行排序，然后从左到右进行排序，依次访问即可：
  • 由于两个不同方向的机器人相遇时必定至少会有一个方向的机器人被移除，因此我们可以用栈保存当前相反方向的机器人编号；
    • 从左到右依次访问时，假如遇到向左行走的机器人，此时栈中保留的是向右行走的机器人，依次从栈中取出机器人，比较二者的健康度，然后移除即可；
  • 如果遇到向右行走的机器人，则将其压入栈中；
  1. 复杂度分析：
  • 时间复杂度：$O(n \log n)$，其中 $n$ 表示机器人的数目。
  • 空间复杂度：$O(n)$，其中 $n$ 表示机器人的数目。

代码

class Solution {
public:
    vector<int> survivedRobotsHealths(vector<int>& positions, vector<int>& healths, string directions) {
        int n = positions.size();
        vector<tuple<int, int, int>> arr;
        for (int i = 0; i < n; i++) {
            arr.emplace_back(positions[i], healths[i], i);
        }
        sort(arr.begin(), arr.end());
        stack<int> st;
        for (int i = 0; i < n; i++) {
            auto [p, h, idx] = arr[i];
            if (directions[idx] == 'L') {
                if (!st.empty()) {
                    while (healths[idx] > 0 && !st.empty()) {
                        if (healths[st.top()] < healths[idx]) {
                            healths[idx]--;
                            healths[st.top()] = 0;
                            st.pop();
                        } else if (healths[st.top()] == healths[idx]) {
                            healths[idx] = 0;
                            healths[st.top()] = 0;
                            st.pop();
                        } else {
                            healths[st.top()]--;
                            healths[idx] = 0;
                        }
                    }
                }
            } else {
                st.emplace(idx);
            }
        }
        vector<int> res;
        for (int i = 0; i < n; i++) {
            if (healths[i] > 0) {
                res.emplace_back(healths[i]);
            }
        }
        return res;
    }
};

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← 【CMU 15-445/645】lec6 leetcode biweekly contes 107 →

扫描二维码，分享此文章