leetcode weekly contes 348

周赛的题目质量还是不错的题目，四个题目比较中规中矩，也没有特别难的超纲题目，但都不是特别水的题目。

6462. 最小化字符串长度

给你一个下标从 0 开始的字符串 s ，重复执行下述操作任意次：

在字符串中选出一个下标 i ，并使 c 为字符串下标 i 处的字符。并在 i 左侧（如果有）和右侧（如果有）各删除一个距离 i 最近的字符 c 。

请你通过执行上述操作任意次，使 s 的长度 最小化 。

返回一个表示 最小化 字符串的长度的整数。

示例 1：

输入：s = "aaabc"
输出：3
解释：在这个示例中，s 等于 "aaabc" 。我们可以选择位于下标 1 处的字符 'a' 开始。接着删除下标 1 左侧最近的那个 'a'（位于下标 0）以及下标 1 右侧最近的那个 'a'（位于下标 2）。执行操作后，字符串变为 "abc" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 3 。

示例 2：

输入：s = "cbbd"
输出：3
解释：我们可以选择位于下标 1 处的字符 'b' 开始。下标 1 左侧不存在字符 'b' ，但右侧存在一个字符 'b'（位于下标 2），所以会删除位于下标 2 的字符 'b' 。执行操作后，字符串变为 "cbd" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 3 。

示例 3：

输入：s = "dddaaa"
输出：2
解释：我们可以选择位于下标 1 处的字符 'd' 开始。接着删除下标 1 左侧最近的那个 'd'（位于下标 0）以及下标 1 右侧最近的那个 'd'（位于下标 2）。执行操作后，字符串变为 "daaa" 。继续对新字符串执行操作，可以选择位于下标 2 的字符 'a' 。接着删除下标 2 左侧最近的那个 'a'（位于下标 1）以及下标 2 右侧最近的那个 'a'（位于下标 3）。执行操作后，字符串变为 "da" 。继续对字符串执行任何操作都不会改变其长度。因此，最小化字符串的长度是 2 。

提示：

1 <= s.length <= 100
s 仅由小写英文字母组成

地址

https://leetcode.cn/contest/weekly-contest-348/problems/minimize-string-length/

题意

模拟

思路

根据题目可以知道，每次去除时，只要存在相同的字符则可以进行删除操作，直到某种字符只剩下一个时则无法删除，因此最终的字符的长度也即等于字符串中不同字符的数目，因为每种不同的字符最终删除后都只剩下一个字符。
复杂度分析：

时间复杂度：$O(n)$，$n$ 表示字符串的长度。
空间复杂度：$O(|\Sigma|)$, 其中 $|\Sigma|$ 表示字符集的数目。

代码

class Solution {
public:
    int minimizedStringLength(string s) {
        unordered_set<char> cnt;
        for (char c : s) {
            cnt.emplace(c);
        }
        return cnt.size();
    }
};

6424. 半有序排列

给你一个下标从 0 开始、长度为 n 的整数排列 nums 。

如果排列的第一个数字等于 1 且最后一个数字等于 n ，则称其为 半有序排列 。你可以执行多次下述操作，直到将 nums 变成一个 半有序排列 ：

选择 nums 中相邻的两个元素，然后交换它们。

返回使 nums 变成 半有序排列 所需的最小操作次数。

排列是一个长度为 n 的整数序列，其中包含从 1 到 n 的每个数字恰好一次。

示例 1：

输入：nums = [2,1,4,3]
输出：2
解释：可以依次执行下述操作得到半有序排列：
1 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
2 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 2 次的方案。

示例 2：

输入：nums = [2,4,1,3]
输出：3
解释：
可以依次执行下述操作得到半有序排列：
1 - 交换下标 1 和下标 2 对应元素。排列变为 [2,1,4,3] 。
2 - 交换下标 0 和下标 1 对应元素。排列变为 [1,2,4,3] 。
3 - 交换下标 2 和下标 3 对应元素。排列变为 [1,2,3,4] 。
可以证明，要让 nums 成为半有序排列，不存在执行操作少于 3 次的方案。

示例 3：

输入：nums = [1,3,4,2,5]
输出：0
解释：这个排列已经是一个半有序排列，无需执行任何操作。

提示：

2 <= nums.length == n <= 50
1 <= nums[i] <= 50
nums 是一个排列

地址

https://leetcode.cn/contest/weekly-contest-348/problems/semi-ordered-permutation/

题意

模拟

思路

根据题意分析可以知道假设 $1$ 出现的位置为 $\text{first}$, $n$ 出现的位置为 $\text{second}$，则分为以下两种情形来分析：
- 如果满足 $\text{first} < \text{second}$，则可以知道需要将 $1$ 依次相邻移动 $\text{first}$ 个位置，$\text{second}$ 需要向右移动 $n - 1 - \text{second}$ 步，总共需要移动 $first + n - 1 - second$ 次；
- 如果满足 $\text{first} > \text{second}$，则可以知道需要将 $1$ 依次相邻移动 $\text{first}$ 个位置，此时 $n$ 会向右移动一步，移动到 $\text{second} + 1$ ，此时 $n$ 还需要向右移动 $n - 2 - \text{second}$ 步，总共需要移动 $first + n - 2 - second$ 次；
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 表示数组的长度。
空间复杂度：$O(1)$。

代码

class Solution {
public:
    int semiOrderedPermutation(vector<int>& nums) {
        int first = 0, last = 0;
        int n = nums.size();
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                first = i;
            }
            if (nums[i] == n) {
                last = i;
            }
        }
        int ans = first + n - 1 - last;
        return first < last ? ans : (ans - 1);
    }
};

6472. 查询后矩阵的和

给你一个整数 n 和一个下标从 0 开始的 二维数组 queries ，其中 queries[i] = [typei, indexi, vali] 。

一开始，给你一个下标从 0 开始的 n x n 矩阵，所有元素均为 0 。每一个查询，你需要执行以下操作之一：

如果 typei == 0 ，将第 indexi 行的元素全部修改为 vali ，覆盖任何之前的值。
如果 typei == 1 ，将第 indexi 列的元素全部修改为 vali ，覆盖任何之前的值。

请你执行完所有查询以后，返回矩阵中所有整数的和。

示例 1：

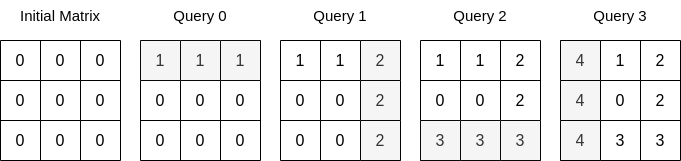
输入：n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]
输出：23
解释：上图展示了每个查询以后矩阵的值。所有操作执行完以后，矩阵元素之和为 23 。

示例 2：

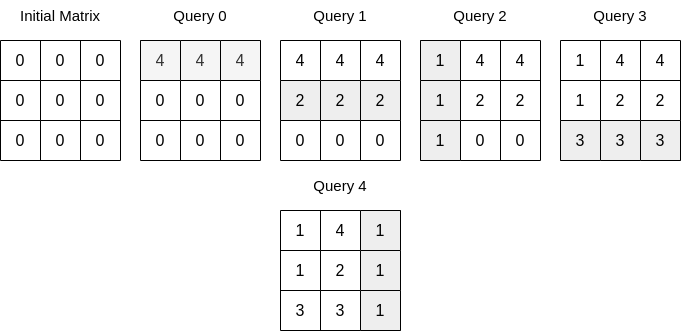
输入：n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]
输出：17
解释：上图展示了每一个查询操作之后的矩阵。所有操作执行完以后，矩阵元素之和为 17 。

提示：

1 <= n <= 104
1 <= queries.length <= 5 * 104
queries[i].length == 3
0 <= typei <= 1
0 <= indexi < n
0 <= vali <= 105

地址

https://leetcode.cn/contest/weekly-contest-348/problems/sum-of-matrix-after-queries/

题意

排序、二分查找、双指针、前缀和

思路

首先我们可以记录下每一行最后的被修改后的值，此时用 $row[i]$ 表示第 $i$ 行的值，同时记录 $time[i]$ 表示在第 $time[i]$ 次操作时，会将第 $i$ 的值全部修改为 $row[i]$, 此时如果我们知道 $time[i]$ 之后哪些列被修改即可，假设这些修改的列的和为 $modify$，则此时可以知道第 $i$ 行的和为：
$$
sum[i] = n * val[i] - modify
$$
根据 $1$ 的分析可以知道，我们只需要找到 $time[i]$ 之后被修改的列的和之和即可，此时我们可以利用如下操作，用 $col[i]$ 表示第 $i$ 列的值，同时记录 $timeCol[i]$ 表示在第 $timeCol[i]$ 次操作时，会将第 $i$ 列的值全部修改为 $col[i]$, 此时我们自然而然想到了排序操作，我们可以将所有列的修改的值按照修改时间的先后进行排序，此时我们可以用二分查找查找所有大于 $time[i]$ 且被修改过的列的值之和，此时我们可以利用前缀和即可在 $O(\log n)$ 的时间复杂度内求出所有在 $time[i]$ 以后被修改的列的值之和，同时加上该行中未被修改的列的值即可。
上述的同样的二分查找的思路我们还可以用双指针的解法即可。
同样还有一种倒序遍历的思路，倒序遍历时，每次查找已经被修改的值则保持不变，否则只统计当前查询可以修改的值之和即可。
复杂度分析：

时间复杂度：$O(q + n \log n)$，其中 $n$ 为矩阵的行数；
空间复杂度：$O(n)$，其中 $n$ 为矩阵的行数；

代码

class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& queries) {
        vector<pair<int, int>> row(n, {-1, 0});
        vector<pair<int, int>> col(n, {-1, 0});
        int m = queries.size();
        for (int i = 0; i < m; i++) {
            int type = queries[i][0];
            int index = queries[i][1];
            int val = queries[i][2];
            if (type == 0) {
                row[index] = make_pair(i, val);
            } else {
                col[index] = make_pair(i, val);
            }
        }
        sort(col.begin(), col.end());
        sort(row.begin(), row.end());
        vector<long long> sum(n + 1);
        for (int i = 0; i < n; i++) {
            sum[i + 1] = sum[i] + col[i].second;
        }
        long long res = 0;
        for (int i = 0, j = 0; i < n; i++) {
            auto [time, val] = row[i];
            while (j < n && col[j].first < time) {
                j++;
            }
            res += (long long) val * j;
            res += sum[n] - sum[j];
        }
        return res;
    }
};

class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& queries) {
        vector<pair<int, int>> row(n, {-1, 0});
        vector<pair<int, int>> col(n, {-1, 0});
        int m = queries.size();
        for (int i = 0; i < m; i++) {
            int type = queries[i][0];
            int index = queries[i][1];
            int val = queries[i][2];
            if (type == 0) {
                row[index] = make_pair(i, val);
            } else {
                col[index] = make_pair(i, val);
            }
        }
        sort(col.begin(), col.end());
        vector<long long> sum(n + 1);
        for (int i = 0; i < n; i++) {
            sum[i + 1] = sum[i] + col[i].second;
        }
        long long res = 0;
        for (int i = 0; i < n; i++) {
            auto [time, val] = row[i];
            int x = upper_bound(col.begin(), col.end(), make_pair(time, 0)) - col.begin();
            res += (long long) x * val;
            res += sum[n] - sum[x];
        }
        return res;
    }
};

class Solution {
public:
    long long matrixSumQueries(int n, vector<vector<int>>& queries) {
        vector<unordered_set<int>> cnt(2);
        long long res = 0;
        for (int i = queries.size() - 1; i >= 0; i--) {
            int type = queries[i][0];
            int index = queries[i][1];
            int val = queries[i][2];
            if (cnt[type].count(index)) continue;
            res += (long long)(n - cnt[type ^ 1].size()) * val;
            cnt[type].emplace(index);
        }
        return res;
    }
};

6396. 统计整数数目

给你两个数字字符串 num1 和 num2 ，以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件，我们称它是一个好整数：

num1 <= x <= num2
min_sum <= digit_sum(x) <= max_sum.

请你返回好整数的数目。答案可能很大，请返回答案对 109 + 7 取余后的结果。

注意，digit_sum(x) 表示 x 各位数字之和。

示例 1：

输入：num1 = "1", num2 = "12", min_num = 1, max_num = 8
输出：11
解释：总共有 11 个整数的数位和在 1 到 8 之间，分别是 1,2,3,4,5,6,7,8,10,11 和 12 。所以我们返回 11 。

示例 2：

输入：num1 = "1", num2 = "5", min_num = 1, max_num = 5
输出：5
解释：数位和在 1 到 5 之间的 5 个整数分别为 1,2,3,4 和 5 。所以我们返回 5 。

提示：

1 <= num1 <= num2 <= 1022
1 <= min_sum <= max_sum <= 400

地址

https://leetcode.cn/contest/weekly-contest-347/problems/maximum-strictly-increasing-cells-in-a-matrix/

题意

数位 dp

思路

拿到这个题目很容易想到数位 $dp$ 的思路，题目初看起来很难，实际上可以进行分解即可，如果直接求的话会非常麻烦，但是实际上可以将其分为几个子问题即可。设 $f(x, val) $ 表示小于等于 $x$ 且所有数字之和不超过 $val$ 的字符串的种类数目，则题目所求可以转换为如下:

所有小于等于 $num1$ 且数字之和大于等于 $min_num$ 且小于等于 $max_num$ 的整数数目为 $f(num1, max_num) - f(num1, min_num - 1)$；
所有小于等于 $num2$ 且数字之和大于等于 $min_num$ 且小于等于 $max_num$ 的整数数目为 $f(num2, max_num) - f(num2, min_num - 1)$；
根据题意可知 $num1 \le num2$，则可以知道所有小于等于 $num2$ 且数字之和大于等于 $min_num$ 且小于等于 $max_num$ 的整数数目一定包含所有小于等于 $num1$ 且数字之和大于等于 $min_num$ 且小于等于 $max_num$ 的整数，我们利用容斥原理将部重复的数据减去即可，此时则题目的答案则变为了如下：
$$
f(num2, max_num) - f(num2, min_num - 1) - (f(num1, max_num) - f(num1, min_num - 1))
$$

根据 $1$ 的分析可以知道题目就变得简单多了，我们只需要利用数位 $dp$ 求出所有小于等于给定的数字 $x$ 且数字之和小于等于 $val$ 的数字数目即可，此时就可以利用数位 $dp$ 的模板即可
复杂度分析：

时间复杂度：$O(n\times \min(n,m))$，其中 $n$ 表示字符串的长度，$m$ 表示给定的数字；
空间复杂度：$O(n\times \min(n,m))$，其中 $n$ 表示字符串的长度，$m$ 表示给定的数字；

代码

class Solution {
public: 
    const int MOD = 1e9 + 7;

    int f(const string &s, int max_sum) {
        int n = s.size();
        int m = min(n * 9, max_sum);
        vector<vector<int>> memo(n, vector<int>(m + 1, -1));

        function<int(int, int, bool)> dfs = [&](int pos, int sum, bool is_limit) -> int {
            if (sum > max_sum) {
                return 0;
            }
            if (pos == n) {
                return 1;
            }
            if (!is_limit && memo[pos][sum] != -1) {
                return memo[pos][sum];
            }
            int res = 0;
            int up = is_limit ? s[pos] - '0' : 9;
            for (int i = 0; i < up; i++) {
                res = (res + dfs(pos + 1, sum + i, false)) % MOD;
            }
            if (is_limit) {
                res = (res + dfs(pos + 1, sum + up, true)) % MOD;
            } else {
                res = (res + dfs(pos + 1, sum + up, false)) % MOD;
                memo[pos][sum] = res;
            }
            return res;
        };
        return dfs(0, 0, true);
    } 

    int count(string num1, string num2, int min_sum, int max_sum) {
        long long sum1 = (f(num1, max_sum) - f(num1, min_sum - 1) + MOD) % MOD;
        long long sum2 = (f(num2, max_sum) - f(num2, min_sum - 1) + MOD) % MOD;
        int res = 0;
        int tot = accumulate(num1.begin(), num1.end(), 0) - static_cast<int>('0') * num1.size();
        if (tot >= min_sum && tot <= max_sum) {
            res++;
        }
        return (res + sum2 - sum1 + MOD) % MOD;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

← leetcode weekly contes 350 leetcode weekly contes 349 →

扫描二维码，分享此文章