leetcode weekly contes 347

周赛的题目还算不错，质量挺高，T3 比较有意思的思考题目。

6457. 移除字符串中的尾随零

给你一个用字符串表示的正整数 num ，请你以字符串形式返回不含尾随零的整数 num 。

示例 1：

输入：num = "51230100"
输出："512301"
解释：整数 "51230100" 有 2 个尾随零，移除并返回整数 "512301" 。

示例 2：

输入：num = "123"
输出："123"
解释：整数 "123" 不含尾随零，返回整数 "123" 。

提示：

1 <= num.length <= 1000
num 仅由数字 0 到 9 组成
num 不含前导零

地址

https://leetcode.cn/contest/weekly-contest-347/problems/remove-trailing-zeros-from-a-string/

题意

模拟

思路

直接模拟即可，直接移除末尾的 $0$ 即可。
复杂度分析：

时间复杂度：$O(n)$，$n$ 表示字符串的长度。
空间复杂度：$O(1)$。

代码

class Solution {
public:
    string removeTrailingZeros(string num) {
        for (int i = num.size() - 1; i >= 0; i--) {
            if (num[i] == '0') {
                num.pop_back();
            } else {
                break;
            }
        }
        return num;
    }
};

2711. 对角线上不同值的数量差

给你一个下标从 0 开始、大小为 m x n 的二维矩阵 grid ，请你求解大小同样为 m x n 的答案矩阵 answer 。

矩阵 answer 中每个单元格 (r, c) 的值可以按下述方式进行计算：

令 topLeft[r][c] 为矩阵 grid 中单元格 (r, c) 左上角对角线上 不同值 的数量。
令 bottomRight[r][c] 为矩阵 grid 中单元格 (r, c) 右下角对角线上 不同值 的数量。

然后 answer[r][c] = |topLeft[r][c] - bottomRight[r][c]| 。

返回矩阵 answer 。

矩阵对角线 是从最顶行或最左列的某个单元格开始，向右下方向走到矩阵末尾的对角线。

如果单元格 (r1, c1) 和单元格 (r, c) 属于同一条对角线且 r1 < r ，则单元格 (r1, c1) 属于单元格 (r, c) 的左上对角线。类似地，可以定义右下对角线。

示例 1：

输入：grid = [[1,2,3],[3,1,5],[3,2,1]]
输出：[[1,1,0],[1,0,1],[0,1,1]]
解释：第 1 个图表示最初的矩阵 grid 。 
第 2 个图表示对单元格 (0,0) 计算，其中蓝色单元格是位于右下对角线的单元格。
第 3 个图表示对单元格 (1,2) 计算，其中红色单元格是位于左上对角线的单元格。
第 4 个图表示对单元格 (1,1) 计算，其中蓝色单元格是位于右下对角线的单元格，红色单元格是位于左上对角线的单元格。
- 单元格 (0,0) 的右下对角线包含 [1,1] ，而左上对角线包含 [] 。对应答案是 |1 - 0| = 1 。
- 单元格 (1,2) 的右下对角线包含 [] ，而左上对角线包含 [2] 。对应答案是 |0 - 1| = 1 。
- 单元格 (1,1) 的右下对角线包含 [1] ，而左上对角线包含 [1] 。对应答案是 |1 - 1| = 0 。
其他单元格的对应答案也可以按照这样的流程进行计算。

示例 2：

输入：grid = [[1]]
输出：[[0]]
解释：- 单元格 (0,0) 的右下对角线包含 [] ，左上对角线包含 [] 。对应答案是 |0 - 0| = 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n, grid[i][j] <= 50

地址

https://leetcode.cn/contest/weekly-contest-347/problems/difference-of-number-of-distinct-values-on-diagonals/

题意

模拟 + 哈希

思路

题目太长，过于啰嗦，本身题目比较简单，每次统计 $(i,j)$ 的左上对角线中的元素个数与右下对角线中的元素个数即可，此时可以用哈希统计即可，每次填充二者的差的绝对值即可。
复杂度分析：

时间复杂度：$O(m \times n \times \min(m, n))$，其中 $m,n$ 分别为矩阵的行数与列数。
空间复杂度：$O(\min(m, n))$, 其中 $m,n$ 分别为矩阵的行数与列数。

代码

class Solution {
public:
    vector<vector<int>> differenceOfDistinctValues(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> res(m, vector<int>(n));
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                /* top left */
                unordered_set<int> cnt1, cnt2;
                for (int x = i - 1, y = j - 1; x >= 0 && y >= 0; x--, y--) {
                    cnt1.emplace(grid[x][y]);
                }
                /* buttom right */
                for (int x = i + 1, y = j + 1; x < m && y < n; x++, y++) {
                    cnt2.emplace(grid[x][y]);
                }
                res[i][j] = abs(static_cast<int>(cnt1.size() - cnt2.size()));
            }
        }
        
        return res;
    }
};

6455. 使所有字符相等的最小成本

给你一个下标从 0 开始、长度为 n 的二进制字符串 s ，你可以对其执行两种操作：

选中一个下标 i 并且反转从下标 0 到下标 i（包括下标 0 和下标 i ）的所有字符，成本为 i + 1 。
选中一个下标 i 并且反转从下标 i 到下标 n - 1（包括下标 i 和下标 n - 1 ）的所有字符，成本为 n - i 。

返回使字符串内所有字符相等需要的 最小成本 。

反转字符意味着：如果原来的值是 ‘0’ ，则反转后值变为 ‘1’ ，反之亦然。

示例 1：

输入：s = "0011"
输出：2
解释：执行第二种操作，选中下标 i = 2 ，可以得到 s = "0000" ，成本为 2 。可以证明 2 是使所有字符相等的最小成本。

示例 2：

输入：s = "010101"
输出：9
解释：执行第一种操作，选中下标 i = 2 ，可以得到 s = "101101" ，成本为 3 。
执行第一种操作，选中下标 i = 1 ，可以得到 s = "011101" ，成本为 2 。
执行第一种操作，选中下标 i = 0 ，可以得到 s = "111101" ，成本为 1 。
执行第二种操作，选中下标 i = 4 ，可以得到 s = "111110" ，成本为 2 。
执行第一种操作，选中下标 i = 5 ，可以得到 s = "111111" ，成本为 1 。
使所有字符相等的总成本等于 9 。可以证明 9 是使所有字符相等的最小成本。

提示：

1 <= s.length == n <= 105
s[i] 为 '0' 或 '1'

地址

https://leetcode.cn/contest/weekly-contest-347/problems/minimum-cost-to-make-all-characters-equal/

题意

贪心或者动态规划

思路

首先我们想到的前后缀分离，最优解一定是要么全部变为 $0$，要么全部变为 $1$,可能以下三种情况之一:
- 全部采用第一种操作变为相同的字符；
- 全部采用第二种操作变为相同的字符；
- 前 $i$ 个采用第一种操作，后 $n-i$ 个字符采用第二种操作；
设 $dpl[i][0],dpl[i][1]$ 表示将前 $i$ 个字符全部变为 $0,1$ 的最少代价，设 $dpr[i][0],dpr[i][1]$ 表示将从 $i$ 开始后面的字符全部变为 $0,1$ 的最少代价，此时可以得到递推公式如下：
- 如果当前字符 $s[i] = \text{`0’}$:
  - 如果前 $i$ 个字符全部转化为 $0$：
    - 如果前 $i-1$ 个字符全为 $\text{`0’}$，此时可以知道不需要反转即可 $dpl[i][0] = \min(dpl[i][0], dpl[i-1][0])$；
    - 如果前 $i-1$ 个字符全为 $\text{`1’}$，此时需要将前 $i-1$ 个字符翻转，此时 $dpl[i][0] = \min(dpl[i][0], dpl[i-1][1] + i)$；
  - 如果前 $i$ 个字符全部转化为 $1$：
    - 如果前 $i-1$ 个字符全为 $\text{`0’}$，此时可以知道前 $i$ 个字符全部需要反转 $dpl[i][1] = \min(dpl[i][1], dpl[i-1][0] + i + 1)$；
    - 如果前 $i-1$ 个字符全为 $\text{`1’}$，此时需要将前 $i$ 个字符翻转，再翻转前 $i-1$ 个字符，此时 $dpl[i][1] = \min(dpl[i][1], dpl[i-1][1] + i * 2 - 1)$；
- 同样的推理过程我们也可以得到 $s[i] = \text{`1’}$ 的解法，第二种操作下的递推公式与原理，在此不再描述该过程。
贪心解法：该解法思考过程还是较难出现前后不同的地方一定会进行一次翻转，要么采用第一种翻转方式要么采用第二种翻转方式，因此我们每次只取最小的翻转即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 为字符串的长度；
空间复杂度：$O(n)$，其中 $n$ 为字符串的长度；

代码

class Solution {
public:
    long long minimumCost(string s) {
        int n = s.size();
        vector<vector<long long>> dpl(n, vector<long long>(2, INT_MAX));
        vector<vector<long long>> dpr(n, vector<long long>(2, INT_MAX));
        for (int i = 0; i < n; i++) {
            if (s[i] == '0') {
                if (i == 0) {
                    dpl[i][0] = 0;
                    dpl[i][1] = 1;
                } else {
                    dpl[i][0] = min(dpl[i - 1][0], dpl[i - 1][1] + i);
                    dpl[i][1] = min(dpl[i - 1][0] + i + 1, dpl[i - 1][1] + 2 * i + 1);
                }
            } else {
                if (i == 0) {
                    dpl[i][0] = 1;
                    dpl[i][1] = 0;
                } else {
                    dpl[i][1] = min(dpl[i - 1][1], dpl[i - 1][0] + i);
                    dpl[i][0] = min(dpl[i - 1][1] + i + 1, dpl[i - 1][0] + 2 * i + 1);
                }
            }
        }
        for (int i = n - 1; i >= 0; i--) {
            if (s[i] == '0') {
                if (i == n - 1) {
                    dpr[i][0] = 0;
                    dpr[i][1] = 1;
                } else {
                    dpr[i][0] = min(dpr[i + 1][0], dpr[i + 1][1] + n - i - 1);
                    dpr[i][1] = min(dpr[i + 1][0] + n - i, dpr[i + 1][1] + 2 * (n - i) - 1);
                }
            } else {
                if (i == n - 1) {
                    dpr[i][0] = 1;
                    dpr[i][1] = 0;
                } else {
                    dpr[i][1] = min(dpr[i + 1][1], dpr[i + 1][0] + n - i - 1);
                    dpr[i][0] = min(dpr[i + 1][1] + n - i, dpr[i + 1][0] + 2 * (n - i) - 1);
                }
            }
        }
        
        long long res = INT_MAX;
        for (int i = 0; i < n; i++) {
            if (i == 0) {
                res = min(dpr[i][0], dpr[i][1]);
            } else if (i == n - 1) {
                res = min({res, dpl[i][0], dpl[i][1]});
            } else {
                res = min(res, dpl[i][0] + dpr[i + 1][0]);
                res = min(res, dpl[i][1] + dpr[i + 1][1]);
            }
        }
        return res;
    }
};

class Solution {
public:
    long long minimumCost(string s) {
        long long ans = 0;
        int n = s.length();
        for (int i = 1; i < n; i++)
            if (s[i - 1] != s[i])
                ans += min(i, n - i);
        return ans;
    }
};

6456. 矩阵中严格递增的单元格数

给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为 起始单元格 。

从起始单元格出发，你可以移动到 同一行或同一列 中的任何其他单元格，但前提是目标单元格的值 严格大于 当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。

返回一个表示可访问单元格最大数量的整数。

示例 1：

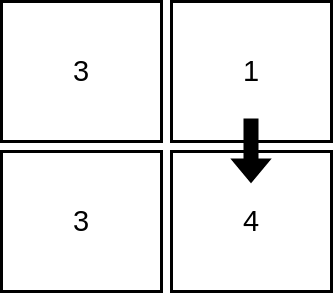
输入：mat = [[3,1],[3,4]]
输出：2
解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。

示例 2：

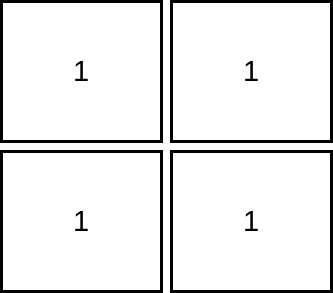
输入：mat = [[1,1],[1,1]]
输出：1
解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。

示例 3：

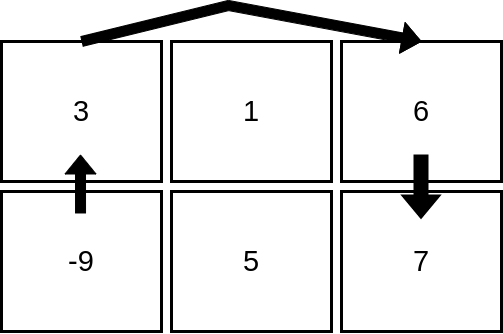
输入：mat = [[3,1,6],[-9,5,7]]
输出：4
解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 105
1 <= m * n <= 105
-105 <= mat[i][j] <= 105

地址

https://leetcode.cn/contest/weekly-contest-347/problems/maximum-strictly-increasing-cells-in-a-matrix/

题意

排序 + 动态规划

思路

拿到题目刚开始想到的就是跳跃游戏的变种而已，由于跳跃时要求数字严格递增，因此我们很容易写出 $O(mn\times(m + n))$ 的解法，将整个矩阵的元素按照从小到大进行排序后，此时我们很容易想到每个元素只能在同一行或者同一列中跳跃，因此很容易的写出如下解法：
- 设 $dp[x][y]$ 表示当前到达 $(x,y)$ 时可以跳跃的最大步数，此时可以找到如下递推关系：
  - 我们可以检测当前第 $x$ 行中的元素大于 $mat[x][y]$, 即满足 $mat[x][k] > mat[x][y]$, 此时 $dp[x][k] = \max(dp[x][k], dp[x][y] + 1)$;
  - 我们可以检测当前第 $y$ 行中的元素大于 $mat[x][y]$, 即满足 $mat[k][y] > mat[x][y]$, 此时 $dp[x][k] = \max(dp[k][y], dp[x][y] + 1)$;
  - 上述方法是最容易想到的动态规划的解法，但是非常不幸的是会超时，因此我们还需要进一步优化；
- 假设我们将所有的元素严格按照大小进行排列，设当前 $row[x]$ 表示当前 $x$ 行中的最大跳跃步数，$row[y]$ 表示当前 $y$ 列中的最大跳跃步数，假设当前我们遍历当元素 $mat[x][y]$ 时，此时我们知道 $mat[x][y]$ 一定满足严格大于所有 $x$ 行中已经遍历过的元素，同时也严格大于 $y$ 列中已经遍历过的元素，因此我们只需要知道当前 $x$ 行或者 $y$ 列的最大值即可，此时可以得到递推关系：
  - $dp[x][y] = \max(row[x], col[y]) + 1$;
  - 当我们更新所有与 $dp[x][y]$ 相等的元素后，再次需要更新 $row[x], col[y]$ 即可；
复杂度分析：

时间复杂度：$O(mn\log (mn)$，其中 $m,n$ 为给定的矩阵的长与宽；
空间复杂度：$O(mn)$，其中 $m,n$ 为给定的矩阵的长与宽；

代码

class Solution {
public:
    int maxIncreasingCells(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        map<int, vector<pair<int, int>>> cnt;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                cnt[mat[i][j]].emplace_back(i, j);
            }
        }
        vector<vector<int>> dp(m, vector<int>(n, 1));
        vector<int> row(m);
        vector<int> col(n);
        for (auto [_, vec] : cnt) {
            for (auto [x, y] : vec) {
                dp[x][y] = max(row[x], col[y]) + 1;
            }
            for (auto [x, y] : vec) {
                row[x] = max(row[x], dp[x][y]);
                col[y] = max(col[y], dp[x][y]);
            }
        }
        return max(*max_element(row.begin(), row.end()), *max_element(col.begin(), col.end()));
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 题解力扣周赛赛

← leetcode biweekly contes 105 【CMU 15-445/645】lec3 →

扫描二维码，分享此文章