leetcode weekly contes 346
难得见到难度较高的第四题了,还是非常好的题目了。
6439. 删除子串后的字符串最小长度
给你一个仅由 大写 英文字符组成的字符串 s 。
你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 任一个 "AB" 或 "CD" 子字符串。
通过执行操作,删除所有 "AB" 和 "CD" 子串,返回可获得的最终字符串的 最小 可能长度。
注意,删除子串后,重新连接出的字符串可能会产生新的 "AB" 或 "CD" 子串。
示例 1:
输入:s = "ABFCACDB" |
示例 2:
输入:s = "ACBBD" |
提示:
1 <= s.length <= 100s仅由大写英文字母组成
地址
题意
栈模拟
思路
- 常规题目,与括号匹配的题目原理基本一样,碰到连续的字母进行出栈即可;
- 复杂度分析:
- 时间复杂度:$O(n)$,$n$ 表示字符的长度。
- 空间复杂度:$O(n)$, $n$ 表示字符串的长度。
代码
class Solution { |
6454. 字典序最小回文串
给你一个由 小写英文字母 组成的字符串 s ,你可以对其执行一些操作。在一步操作中,你可以用其他小写英文字母 替换 s 中的一个字符。
请你执行 尽可能少的操作 ,使 s 变成一个 回文串 。如果执行 最少 操作次数的方案不止一种,则只需选取 字典序最小 的方案。
对于两个长度相同的字符串 a 和 b ,在 a 和 b 出现不同的第一个位置,如果该位置上 a 中对应字母比 b 中对应字母在字母表中出现顺序更早,则认为 a 的字典序比 b 的字典序要小。
返回最终的回文字符串。
示例 1:
输入:s = "egcfe" |
示例 2:
输入:s = "abcd" |
示例 3:
输入:s = "seven" |
提示:
1 <= s.length <= 1000s仅由小写英文字母组成
地址
https://leetcode.cn/contest/weekly-contest-346/problems/lexicographically-smallest-palindrome/
题意
贪心算法
思路
- 题目首先要求替换次数最少,然后要求字典序最小,我们依次比较 $s[i]$ 与 $s[n-1-i]$ 的两个字符是否相等:
- 如果两个字符相等则跳过;
- 如果不相等,则将两个字符中较大的字符替换为较小的字符即可;
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为字符串的长度。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6441. 求一个整数的惩罚数
给你一个正整数 n ,请你返回 n 的 惩罚数 。
n 的 惩罚数 定义为所有满足以下条件 i 的数的平方和:
1 <= i <= ni * i的十进制表示的字符串可以分割成若干连续子字符串,且这些子字符串对应的整数值之和等于i。
示例 1:
输入:n = 10 |
示例 2:
输入:n = 37 |
提示:
1 <= n <= 1000
地址
https://leetcode.cn/contest/weekly-contest-346/problems/find-the-punishment-number-of-an-integer/
题意
回溯
思路
- 题目比较简单了,由于给定的 $n$ 的范围为 $[1,1000]$,所以我们依次检测 $i \in [1,n]$ 是否属于惩罚数即可。
- 检测惩罚数时我们可以采取深度优先搜索加减枝即可,比较简单的题目了;
- 复杂度分析:
- 时间复杂度:$O(n \times 2 ^{\log_{10}^{U}})$,其中 $n$ 为给定的元素
- 空间复杂度:$O(U)$.
代码
class Solution { |
6442. 修改图中的边权
给你一个 n 个节点的 无向带权连通 图,节点编号为 0 到 n - 1 ,再给你一个整数数组 edges ,其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。
部分边的边权为 -1(wi = -1),其他边的边权都为 正 数(wi > 0)。
你需要将所有边权为 -1 的边都修改为范围 [1, 2 * 109] 中的 正整数 ,使得从节点 source 到节点 destination 的 最短距离 为整数 target 。如果有 多种 修改方案可以使 source 和 destination 之间的最短距离等于 target ,你可以返回任意一种方案。
如果存在使 source 到 destination 最短距离为 target 的方案,请你按任意顺序返回包含所有边的数组(包括未修改边权的边)。如果不存在这样的方案,请你返回一个 空数组 。
注意:你不能修改一开始边权为正数的边。
示例 1:
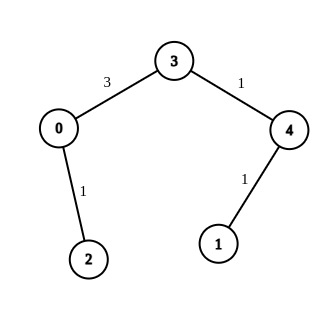
输入:n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5 |
示例 2:
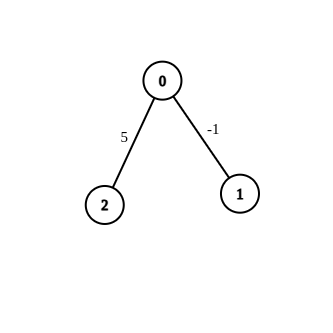
输入:n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6 |
示例 3:
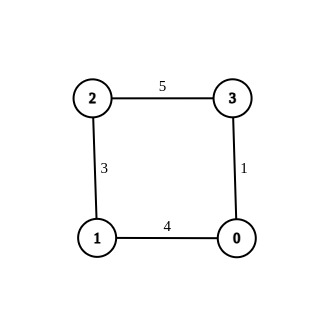
输入:n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6 |
提示:
1 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= ai, bi < nwi = -1或者1 <= wi <= 107ai != bi0 <= source, destination < nsource != destination1 <= target <= 109- 输入的图是连通图,且没有自环和重边。
地址
https://leetcode.cn/contest/weekly-contest-346/problems/modify-graph-edge-weights/
题意
dijkstra算法
思路
- 首先我们需要检测什么样的图可以通过改变边的权重从而使得起点到终点的最小值刚好等于 $target$;
- 假设当前图中从起点且不通过权为 $-1$ 的边到达终点的最小路径 $mindist < target$,在这种情况下,由于该路径无法更改,因此一定存在最小路径的值小于 $target$, 此时直接返回;
- 我们将图中权为 $-1$ 的边的权重全部设置为最小值 $1$,则此时我们找到起点到终点的最小路径和 $mindist > target$,在这种情况下,由于最小的权重下,最短路径的值都大于 $target$,因此一定不存在最小路径的值等于 $target$, 此时直接返回;
- 排查上述两种非法情况后,我们尝试如何来调整边的权重,此时我们首先将所有为负的边均设置为 $\infin$ ,此时我们可以知道此时求的 $source$ 到 $target$ 的最短路径一定是大于 $target$ 的,此时我们需要进行不断尝试:
- 每次尝试将一条边 $\infin$ 设为 $1$, 此时再利用 $dijkstra$ 跑一遍最短路径,如果求得当前起点到终点的最短路径仍然大于 $target$ 则继续;
- 一直尝试到此时出现次数最短距离小于等于 $target$ 为止,此时设 $diff = target - dist$ ,即最短距离与 $target$ 的差值,此时说明当前的边一定在最短路径的关键路径上,因此我们可以将该条边再加上 $diff$ ,此时最短路径就一定为 $target$, 然后返回即可;
- 另外一种解法是反过来,将所有的边全部设为 $1$,每次求最短路径,如果最小距离小于 $target$ ,则将最短路径上的一条权值为负的边加上 $diff$, 一直循环下去,直到最短路径为 $target$ 为止;
- 复杂度分析:
- 时间复杂度:$O(m \times n\log n)$,其中 $n$ 为给定的节点的数目,$m$ 表示边的数目;
- 空间复杂度:$O(n)$,其中 $n$ 为给定的节点的数目;
代码
const int INF = 2 * 1e9; |
class Solution: |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
