且听疯吟

leetcode weekly contes 345

2023-05-21

leetcode weekly contes 345

连续三场均为手速场的题目，看来确实水平有待提高。

2682. 找出转圈游戏输家

n 个朋友在玩游戏。这些朋友坐成一个圈，按 顺时针方向 从 1 到 n 编号。从第 i 个朋友的位置开始顺时针移动 1 步会到达第 (i + 1) 个朋友的位置（1 <= i < n），而从第 n 个朋友的位置开始顺时针移动 1 步会回到第 1 个朋友的位置。

游戏规则如下：

第 1 个朋友接球。

  • 接着，第 1 个朋友将球传给距离他顺时针方向 k 步的朋友。
  • 然后，接球的朋友应该把球传给距离他顺时针方向 2 * k 步的朋友。
  • 接着，接球的朋友应该把球传给距离他顺时针方向 3 * k 步的朋友，以此类推。

换句话说，在第 i 轮中持有球的那位朋友需要将球传递给距离他顺时针方向 i * k 步的朋友。

当某个朋友第 2 次接到球时，游戏结束。

在整场游戏中没有接到过球的朋友是 输家 。

给你参与游戏的朋友数量 n 和一个整数 k ，请按升序排列返回包含所有输家编号的数组 answer 作为答案。

示例 1：

输入：n = 5, k = 2
输出：[4,5]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 2 步的玩家 —— 第 3 个朋友。
2）第 3 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 2 个朋友。
3）第 2 个朋友将球传给距离他顺时针方向 6 步的玩家 —— 第 3 个朋友。
4）第 3 个朋友接到两次球，游戏结束。

示例 2：

输入：n = 4, k = 4
输出：[2,3,4]
解释：以下为游戏进行情况：
1）第 1 个朋友接球，第 1 个朋友将球传给距离他顺时针方向 4 步的玩家 —— 第 1 个朋友。
2）第 1 个朋友接到两次球，游戏结束。

提示：

  • 1 <= k <= n <= 50

地址

https://leetcode.cn/contest/weekly-contest-345/problems/find-the-losers-of-the-circular-game/

题意

直接模拟

思路

  1. 直接按照题目要求模拟即可，第 $i$ 次取出 $x$, 则下一个元素为 $x + i * k$;
  2. 复杂度分析：
  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(n)$。

代码

class Solution {
public:
    vector<int> circularGameLosers(int n, int k) {
        vector<int> ans;
        vector<bool> visit(n);
        queue<int> qu;
        qu.emplace(0);
        visit[0] = true;
        int i = 1;
        while (!qu.empty()) {
            int curr = qu.front();
            qu.pop();
            int next = (curr + k * i) % n;
            i++;
            if (visit[next]) {
                break;
            }
            visit[next] = true;
            qu.emplace(next);
        }
        for (int j = 0; j < n; j++) {
            if (!visit[j]) {
                ans.emplace_back(j + 1);
            }
        }
        return ans;
    }
};

2683. 相邻值的按位异或

下标从 0 开始、长度为 n 的数组 derived 是由同样长度为 n 的原始 二进制数组 original 通过计算相邻值的 按位异或（⊕）派生而来。

特别地，对于范围 [0, n - 1] 内的每个下标 i ：

  • 如果 i = n - 1 ，那么 derived[i] = original[i] ⊕ original[0]
  • 否则 derived[i] = original[i] ⊕ original[i + 1]

给你一个数组 derived ，请判断是否存在一个能够派生得到 derived 的 有效原始二进制数组 original 。

如果存在满足要求的原始二进制数组，返回 true ；否则，返回 false 。

  • 二进制数组是仅由 0 和 1 组成的数组。

示例 1：

输入：derived = [1,1,0]
输出：true
解释：能够派生得到 [1,1,0] 的有效原始二进制数组是 [0,1,0] ：
derived[0] = original[0] ⊕ original[1] = 0 ⊕ 1 = 1 
derived[1] = original[1] ⊕ original[2] = 1 ⊕ 0 = 1
derived[2] = original[2] ⊕ original[0] = 0 ⊕ 0 = 0

示例 2：

输入：derived = [1,1]
输出：true
解释：能够派生得到 [1,1] 的有效原始二进制数组是 [0,1] ：
derived[0] = original[0] ⊕ original[1] = 1
derived[1] = original[1] ⊕ original[0] = 1

示例 3：

输入：derived = [1,0]
输出：false
解释：不存在能够派生得到 [1,0] 的有效原始二进制数组。

提示：

  • n == derived.length
  • 1 <= n <= 105
  • derived 中的值不是 0 就是 1 。

地址

https://leetcode.cn/contest/biweekly-contest-104/problems/sum-in-a-matrix/

题意

直接模拟

思路

  1. 由于每个数字只能为 $0$ 或 $1$,按照题目给定的数字，我们依次尝试 $nums[0] = 0$ 与 $nums[0] = 1$ 两种情况是否符合题目要求即可。
  2. 我们将 $derived$ 数组中的所有的元素进行异或，最终可以得到结果为 $nums[0] \oplus nums[0] = 0$ ，此时两个相同元素异或的结果一定为 $0$，否则为非法数组。
  3. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 为数组的长度。
  • 空间复杂度：$O(n)$，其中 $n$ 为数组的长度。

代码

class Solution {
public:
    bool doesValidArrayExist(vector<int>& derived) {
        return std::accumulate(derived.begin(), derived.end(), 0, std::bit_xor<int>()) == 0;
    }
};

2684. 矩阵中移动的最大次数

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

  • 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

img

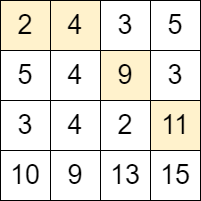
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 105
  • 1 <= grid[i][j] <= 106

地址

https://leetcode.cn/contest/weekly-contest-345/problems/maximum-number-of-moves-in-a-grid/

题意

动态规划或者广度优先搜索

思路

  1. 我们需要观察一下移动规律如下：

    • `(row, col)` 可以移动到 `(row - 1, col + 1)`、`(row, col + 1)` 和 `(row + 1, col + 1)`


         + 我们可以观察到每次移动元素都只会往右边移动一列，因此我们只需要求出当前元素可以移动的最右边列的数目接口知道最多可以移动的步数

      2. 我们采用广度优先搜索即可，每次发现右边相邻的列存在比当前元素大时，则向右移动，最终找到最多移动的列即可；

      3. 复杂度分析：

      + 时间复杂度：$O(mn)$，其中 $mn$ 为给给定的矩阵的行数与列数。
      + 空间复杂度：$O(mn)$，其中 $mn$ 为给定的矩阵的行数与列数。

      #### 代码

      ```C++
      class Solution {
      public:
          int maxMoves(vector<vector<int>>& grid) {
              int dir[3][2] = {{0, 1}, {1, 1}, {-1, 1}};
              int m = grid.size();
              int n = grid[0].size();
              int res = 0;
              vector<vector<bool>> visit(m, vector<bool>(n, false));
              queue<pair<int, int>> qu;
              for (int i = 0; i < m; i++) {
                  qu.emplace(i, 0);
                  visit[i][0] = true;
              }
              while (!qu.empty()) {
                  auto [x, y] = qu.front();
                  qu.pop();
                  res = max(res, y);
                  for (int i = 0; i < 3; i++) {
                      int nx = x + dir[i][0];
                      int ny = y + dir[i][1];
                      if (nx >= 0 && ny >= 0 && nx < m && ny < n && !visit[nx][ny]) {
                          if (grid[nx][ny] > grid[x][y]) {
                              visit[nx][ny] = true;
                              qu.emplace(nx, ny);
                          }
                      }
                  }
              }
              return res;
          }
      };

2685. 统计完全连通分量的数量

给你一个整数 n 。现有一个包含 n 个顶点的 无向 图，顶点按从 0 到 n - 1 编号。给你一个二维整数数组 edges 其中 edges[i] = [ai, bi] 表示顶点 ai 和 bi 之间存在一条 无向 边。

返回图中 完全连通分量 的数量。

如果在子图中任意两个顶点之间都存在路径，并且子图中没有任何一个顶点与子图外部的顶点共享边，则称其为 连通分量 。

如果连通分量中每对节点之间都存在一条边，则称其为 完全连通分量 。

示例 1：

img

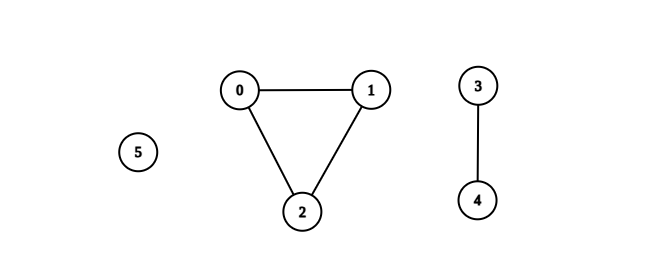
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
输出：3
解释：如上图所示，可以看到此图所有分量都是完全连通分量。

示例 2：

img

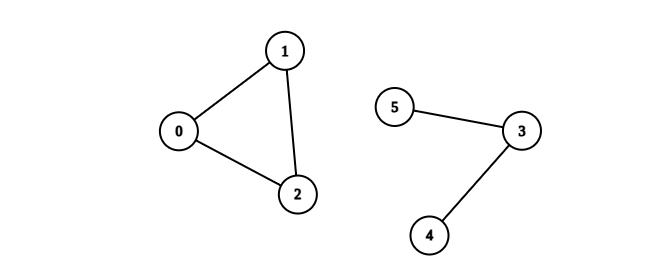
输入：n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
输出：1
解释：包含节点 0、1 和 2 的分量是完全连通分量，因为每对节点之间都存在一条边。
包含节点 3 、4 和 5 的分量不是完全连通分量，因为节点 4 和 5 之间不存在边。
因此，在图中完全连接分量的数量是 1 。

提示：

  • 1 <= n <= 50
  • 0 <= edges.length <= n * (n - 1) / 2
  • edges[i].length == 2
  • 0 <= ai, bi <= n - 1
  • ai != bi
  • 不存在重复的边

地址

https://leetcode.cn/contest/weekly-contest-345/problems/count-the-number-of-complete-components/

题意

简单题目

思路

  1. 题目本身比较简单了，给定的数量又非常小，求完全连通分量实际可以分为以下两个步骤：
    • 求连通分量：我们可以用并查集或者广度优先搜索或者深度优先搜索均可，求出图中的连通分量；
    • 检查完全连通：这个方法就有很多了，由于图中不存在重复的边，假设当前连通分量中存在 $m$ 个节点，则这 $m$ 个节点都含有 $m-1$ 条边即可，这是由于完全连通分量中的每个节点与其他节点都存在一条连接的边；
  2. 复杂度分析：
  • 时间复杂度：$O(n + m)$，其中 $n$ 为给定的节点的数目，$m$ 表示边的数目；
  • 空间复杂度：$O(n)$，其中 $n$ 为给定的节点的数目；

代码

emplace_back

欢迎关注和打赏，感谢支持！

Tags: 题解 力扣周赛赛
← leetcode biweekly contes 104 leetcode weekly contes 346 →

扫描二维码，分享此文章