leetcode weekly contes 344
手速场的题目,可惜的是每次手速场排名都不咋读,也许是年纪大了,思维不够快。非手速场,成绩还好一些。
6416. 找出不同元素数目差数组
给你一个下标从 0 开始的数组 nums ,数组长度为 n 。
nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示,其中 diff[i] 等于前缀 nums[0, ..., i] 中不同元素的数目 减去 后缀 nums[i + 1, ..., n - 1] 中不同元素的数目。
返回 nums 的 不同元素数目差 数组。
注意 nums[i, ..., j] 表示 nums 的一个从下标 i 开始到下标 j 结束的子数组(包含下标 i 和 j 对应元素)。特别需要说明的是,如果 i > j ,则 nums[i, ..., j] 表示一个空子数组。
示例 1:
输入:nums = [1,2,3,4,5]
输出:[-3,-1,1,3,5]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 4 个不同的元素。因此,diff[0] = 1 - 4 = -3 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 3 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 3 - 2 = 1 。
对于 i = 3,前缀中有 4 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 4 - 1 = 3 。
对于 i = 4,前缀中有 5 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 5 - 0 = 5 。
|
示例 2:
输入:nums = [3,2,3,4,2]
输出:[-2,-1,0,2,3]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[0] = 1 - 3 = -2 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 2 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 2 - 2 = 0 。
对于 i = 3,前缀中有 3 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 3 - 1 = 2 。
对于 i = 4,前缀中有 3 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 3 - 0 = 3 。
|
提示:
1 <= n == nums.length <= 501 <= nums[i] <= 50
地址
https://leetcode.cn/contest/weekly-contest-343/problems/determine-the-winner-of-a-bowling-game/
题意
直接模拟
思路
- 直接统计数组前缀与后缀中不同元素的数目即可。
- 复杂度分析:
- 时间复杂度:$O(n)$。
- 空间复杂度:$O(n)$。
代码
class Solution {
public:
vector<int> distinctDifferenceArray(vector<int>& nums) {
int n = nums.size();
unordered_map<int, int> cnt;
unordered_map<int, int> pre;
vector<int> diff;
for (auto v : nums) {
cnt[v]++;
}
for (auto v : nums) {
pre[v]++;
cnt[v]--;
if (cnt[v] == 0) {
cnt.erase(v);
}
diff.emplace_back(pre.size() - cnt.size());
}
return diff;
}
};
|
6417. 频率跟踪器
请你设计并实现一个能够对其中的值进行跟踪的数据结构,并支持对频率相关查询进行应答。
实现 FrequencyTracker 类:
FrequencyTracker():使用一个空数组初始化 FrequencyTracker 对象。void add(int number):添加一个 number 到数据结构中。void deleteOne(int number):从数据结构中删除一个 number 。数据结构 可能不包含 number ,在这种情况下不删除任何内容。bool hasFrequency(int frequency): 如果数据结构中存在出现 frequency 次的数字,则返回 true,否则返回 false。
示例 1:
输入
["FrequencyTracker", "add", "add", "hasFrequency"]
[[], [3], [3], [2]]
输出
[null, null, null, true]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.add(3); // 数据结构现在包含 [3, 3]
frequencyTracker.hasFrequency(2); // 返回 true ,因为 3 出现 2 次
|
示例 2:
输入
["FrequencyTracker", "add", "deleteOne", "hasFrequency"]
[[], [1], [1], [1]]
输出
[null, null, null, false]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.add(1); // 数据结构现在包含 [1]
frequencyTracker.deleteOne(1); // 数据结构现在为空 []
frequencyTracker.hasFrequency(1); // 返回 false ,因为数据结构为空
|
示例 3:
输入
["FrequencyTracker", "hasFrequency", "add", "hasFrequency"]
[[], [2], [3], [1]]
输出
[null, false, null, true]
解释
FrequencyTracker frequencyTracker = new FrequencyTracker();
frequencyTracker.hasFrequency(2); // 返回 false ,因为数据结构为空
frequencyTracker.add(3); // 数据结构现在包含 [3]
frequencyTracker.hasFrequency(1); // 返回 true ,因为 3 出现 1 次
|
提示:
1 <= number <= 1051 <= frequency <= 105- 最多调用
add、deleteOne 和 hasFrequency 共计 2 * 105 次
地址
https://leetcode.cn/contest/weekly-contest-343/problems/first-completely-painted-row-or-column/
题意
模拟
思路
- 直接利用哈希表统计元素的出现次数,并统计元素出现的次数。
- $\texttt{add}$ 操作:直接更新统计次数即可;
- $delete$: 更新统计次数;
- 复杂度分析:
- 时间复杂度:$O(mn)$,其中 $m,n$ 为矩阵的行数与列数。
- 空间复杂度:$O(mn)$,其中 $m,n$ 为矩阵的行数与列数。
代码
class FrequencyTracker {
public:
FrequencyTracker() {
}
void add(int number) {
if (cnt.count(number)) {
int x = cnt[number];
freq[x]--;
if (freq[x] == 0) {
freq.erase(x);
}
cnt[number]++;
freq[x + 1]++;
} else {
cnt[number] = 1;
freq[1]++;
}
}
void deleteOne(int number) {
if (cnt.count(number)) {
int x = cnt[number];
freq[x]--;
if (freq[x] == 0) {
freq.erase(x);
}
cnt[number]--;
if (cnt[number] == 0) {
cnt.erase(number);
}
if (x - 1 > 0) {
freq[x - 1]++;
}
}
}
bool hasFrequency(int frequency) {
return freq.count(frequency);
}
private:
unordered_map<int, int> cnt;
unordered_map<int, int> freq;
};
|
2672. 有相同颜色的相邻元素数目
给你一个下标从 0 开始、长度为 n 的数组 nums 。一开始,所有元素都是 未染色 (值为 0 )的。
给你一个二维整数数组 queries ,其中 queries[i] = [indexi, colori] 。
对于每个操作,你需要将数组 nums 中下标为 indexi 的格子染色为 colori 。
请你返回一个长度与 queries 相等的数组 answer ,其中 answer[i]是前 i 个操作 之后 ,相邻元素颜色相同的数目。
更正式的,answer[i] 是执行完前 i 个操作后,0 <= j < n - 1 的下标 j 中,满足 nums[j] == nums[j + 1] 且 nums[j] != 0 的数目。
示例 1:
输入:n = 4, queries = [[0,2],[1,2],[3,1],[1,1],[2,1]]
输出:[0,1,1,0,2]
解释:一开始数组 nums = [0,0,0,0] ,0 表示数组中还没染色的元素。
- 第 1 个操作后,nums = [2,0,0,0] 。相邻元素颜色相同的数目为 0 。
- 第 2 个操作后,nums = [2,2,0,0] 。相邻元素颜色相同的数目为 1 。
- 第 3 个操作后,nums = [2,2,0,1] 。相邻元素颜色相同的数目为 1 。
- 第 4 个操作后,nums = [2,1,0,1] 。相邻元素颜色相同的数目为 0 。
- 第 5 个操作后,nums = [2,1,1,1] 。相邻元素颜色相同的数目为 2 。
|
示例 2:
输入:n = 1, queries = [[0,100000]]
输出:[0]
解释:一开始数组 nums = [0] ,0 表示数组中还没染色的元素。
- 第 1 个操作后,nums = [100000] 。相邻元素颜色相同的数目为 0 。
|
提示:
1 <= n <= 1051 <= queries.length <= 105queries[i].length == 20 <= indexi <= n - 11 <= colori <= 105
地址
https://leetcode.cn/contest/weekly-contest-344/problems/number-of-adjacent-elements-with-the-same-color/
题意
直接模拟
思路
- 由于每次改变第 $i$ 个元素,此时只会改变 $(i - 1, i),(i, i + 1)$ 这两个数对,我们直接计算前后变换后的数对关系即可,直接模拟即可。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为给定的数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 为给定的数组的长度。
代码
class Solution {
public:
vector<int> colorTheArray(int n, vector<vector<int>>& queries) {
int m = queries.size();
int tot = 0;
vector<int> ans(m);
vector<int> nums(n + 2);
for (int i = 0; i < m; i++) {
int x = queries[i][0] + 1;
int c = queries[i][1];
if (nums[x]) {
tot -= (nums[x - 1] == nums[x]) + (nums[x + 1] == nums[x]);
}
nums[x] = c;
tot += (nums[x - 1] == nums[x]) + (nums[x + 1] == nums[x]);
ans[i] = tot;
}
return ans;
}
};
|
2673. 使二叉树所有路径值相等的最小代价
给你一个整数 n 表示一棵 满二叉树 里面节点的数目,节点编号从 1 到 n 。根节点编号为 1 ,树中每个非叶子节点 i 都有两个孩子,分别是左孩子 2 * i 和右孩子 2 * i + 1 。
树中每个节点都有一个值,用下标从 0 开始、长度为 n 的整数数组 cost 表示,其中 cost[i] 是第 i + 1 个节点的值。每次操作,你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。
你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。
注意:
- 满二叉树 指的是一棵树,它满足树中除了叶子节点外每个节点都恰好有 2 个节点,且所有叶子节点距离根节点距离相同。
- 路径值 指的是路径上所有节点的值之和。
示例 1:
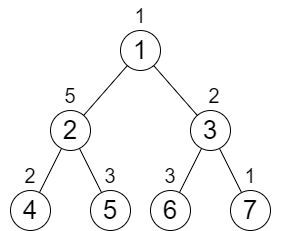
输入:n = 7, cost = [1,5,2,2,3,3,1]
输出:6
解释:我们执行以下的增加操作:
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。
|
示例 2:
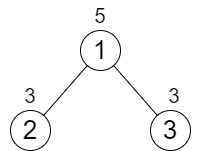
输入:n = 3, cost = [5,3,3]
输出:0
解释:两条路径已经有相等的路径值,所以不需要执行任何增加操作。
|
提示:
3 <= n <= 105n + 1 是 2 的幂cost.length == n1 <= cost[i] <= 104
地址
https://leetcode.cn/contest/weekly-contest-344/problems/make-costs-of-paths-equal-in-a-binary-tree/
题意
贪心
思路
- 题目要求从根节点到所有叶子节点的路径和相等,首先我们可以知道路径和越小,则执行的加法操作肯定越少,首先我们观察一下最小的路径和为多少,此时我们求出所有当前树中从根节点到所有叶子节点的路径和,此时假设最大的路径和为 $distmax$,则此时我们应该在子树中对部分节点执行操作是的从根节点到所有叶子节点的路径和都为 $distmax$;
- 接下来我们需要求出最小操作步数,此时我们可以知道最大步数肯定是在每个叶子节点上执行加法操作即可,但是我们如何贪心的最小操作呢?
- 假设根节点到左子树的叶子节点最大距离为 $distleft$,到右子树的叶子节点的最大距离为 $distright$,则此时根据贪心原则,我们应该在根节点的左孩子上增加 $distmax - distleft$,在根节点的右孩子上增加 $distmax - distright$,这样可以保证所有经过左孩子的路径和全部都会增加 $distmax - distleft$, 所有经过右孩子的路径和全部都会增加 $distmax - distright$,这样即可满足贪心;
- 我们依次将经过当前节点的最大路径和往下传递即可,即可依次计算出该节点增加的值;
- 同时可以参考更为简洁的解法,自底向上的求解,DFS
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为节点的数目;
- 空间复杂度:$O(n)$,其中 $n$ 为节点的数目;
代码
class Solution {
public:
int dfs1(int root, int n, vector<int>& cost, vector<int> &sum) {
sum[root - 1] = cost[root - 1];
if (root * 2 > n) {
return sum[root - 1];
}
sum[root - 1] += max(dfs1(root * 2, n, cost, sum), dfs1(root * 2 + 1, n, cost, sum));
return sum[root - 1];
}
void dfs2(int root, int n, int curr, vector<int> &cost, vector<int> &sum, vector<int> &add) {
int res = 0;
if (root * 2 > n) {
add[root - 1] = curr - sum[root - 1];
return;
}
int left = root * 2;
int right = root * 2 + 1;
add[root - 1] = curr - sum[root - 1];
int tot = curr - add[root - 1] - cost[root - 1];
dfs2(left, n, tot, cost, sum, add);
dfs2(right, n, tot, cost, sum, add);
}
int minIncrements(int n, vector<int>& cost) {
vector<int> sum(n);
vector<int> add(n);
int maxVal = dfs1(1, n, cost, sum);
dfs2(1, n, maxVal, cost, sum, add);
return accumulate(add.begin(), add.end(), 0);
}
};
class Solution {
public:
int minIncrements(int n, vector<int>& cost) {
long long ans = 0;
function<long long(int)> f = [&](int x) {
int L = x * 2, R = x * 2 + 1;
if (L > n) return 1LL * cost[x - 1];
long long a = f(L), b = f(R);
ans += max(a, b) - min(a, b);
return max(a, b) + cost[x - 1];
};
f(1);
return ans;
}
};
|
欢迎关注和打赏,感谢支持!




