leetcode weekly contes 343

题目出的不太好，T3 这个题目出的确实不咋的，虽然没做出来，但是感觉这个题目出的确实不咋的。

2660. 保龄球游戏的获胜者

给你两个下标从 0 开始的整数数组 player1 和 player2 ，分别表示玩家 1 和玩家 2 击中的瓶数。

保龄球比赛由 n 轮组成，每轮的瓶数恰好为 10 。

假设玩家在第 i 轮中击中 xi 个瓶子。玩家第 i 轮的价值为：

如果玩家在前两轮中击中了 10 个瓶子，则为 2xi 。
否则，为 xi 。

玩家的得分是其 n 轮价值的总和。

如果玩家 1 的得分高于玩家 2 的得分，则为 1 ；
如果玩家 2 的得分高于玩家 1 的得分，则为 2 ；
如果平局，则为 0 。

示例 1：

输入：player1 = [4,10,7,9], player2 = [6,5,2,3]
输出：1
解释：player1 的得分是 4 + 10 + 2*7 + 2*9 = 46 。
player2 的得分是 6 + 5 + 2 + 3 = 16 。
player1 的得分高于 player2 的得分，所以 play1 在比赛中获胜，答案为 1 。

示例 2：

输入：player1 = [3,5,7,6], player2 = [8,10,10,2]
输出：2
解释：player1 的得分是 3 + 5 + 7 + 6 = 21 。
player2 的得分是 8 + 10 + 2*10 + 2*2 = 42 。
player2 的得分高于 player1 的得分，所以 play2 在比赛中获胜，答案为 2 。

示例 3：

输入：player1 = [2,3], player2 = [4,1]
输出：0
解释：player1 的得分是 2 + 3 = 5 。
player2 的得分是 4 + 1 = 5 。
player1 的得分等于 player2 的得分，所以这一场比赛平局，答案为 0 。

提示：

n == player1.length == player2.length
1 <= n <= 1000
0 <= player1[i], player2[i] <= 10

地址

https://leetcode.cn/contest/weekly-contest-343/problems/determine-the-winner-of-a-bowling-game/

题意

直接模拟

思路

题目翻译的有问题，应该是前两轮的任意一轮得10分即当前轮的得分翻倍，我们直接模拟即可，判断当前轮的前两轮是否有 10 即可。
复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

代码

class Solution {
public:
    int isWinner(vector<int>& player1, vector<int>& player2) {
        int n = player1.size();
        int s1 = 0, s2 = 0;
        for (int i = 0; i < n; i++) {
            if ((i > 0 && player1[i - 1] == 10) || (i > 1 && player1[i - 2] == 10)) {
                s1 += 2 * player1[i];
            } else {
                s1 += player1[i];
            }
            if ((i > 0 && player2[i - 1] == 10) || (i > 1 && player2[i - 2] == 10)) {
                s2 += 2 * player2[i];
            } else {
                s2 += player2[i];
            }
        }
        if (s1 > s2) {
            return 1;
        } else if (s1 < s2) {
            return 2;
        } else {
            return 0;
        }
    }
};

2661. 找出叠涂元素

给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数矩阵 mat 。arr 和 mat 都包含范围 [1，m * n] 内的所有整数。

从下标 0 开始遍历 arr 中的每个下标 i ，并将包含整数 arr[i] 的 mat 单元格涂色。

请你找出 arr 中在 mat 的某一行或某一列上都被涂色且下标最小的元素，并返回其下标 i 。

示例 1：

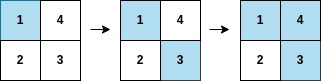
image explanation for example 1

输入：arr = [1,3,4,2], mat = [[1,4],[2,3]]
输出：2
解释：遍历如上图所示，arr[2] 在矩阵中的第一行或第二列上都被涂色。

示例 2：

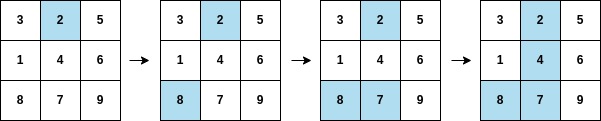
image explanation for example 2

输入：arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
输出：3
解释：遍历如上图所示，arr[3] 在矩阵中的第二列上都被涂色。

提示：

m == mat.length
n = mat[i].length
arr.length == m * n
1 <= m, n <= 105
1 <= m * n <= 105
1 <= arr[i], mat[r][c] <= m * n
arr 中的所有整数 互不相同
mat 中的所有整数 互不相同

地址

https://leetcode.cn/contest/weekly-contest-343/problems/first-completely-painted-row-or-column/

题意

模拟

思路

由于题目中每个元素均不相同，此时我们直接记录每个元素在矩阵中出现的位置 $(x,y)$，每次遍历当前元素 $arr[i]$ 时，我们将其所在的行 $r$ 中的元素数目减 $1$,将其所在的列 $r$ 中的元素数目减 $1$,如果当前行的数目或者列的数目变为 $0$,则返回当前的索引 $i$ 即可。
复杂度分析：

时间复杂度：$O(mn)$，其中 $m,n$ 为矩阵的行数与列数。
空间复杂度：$O(mn)$，其中 $m,n$ 为矩阵的行数与列数。

代码

class Solution {
public:
    int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
        int row = mat.size();
        int col = mat[0].size();
        vector<int> rowCnt(row, col);
        vector<int> colCnt(col, row);
        vector<int> cnt(arr.size() + 1);
        
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                cnt[mat[i][j]] = i * col + j;
            }
        }
        for (int i = 0; i < arr.size(); i++) {
            int r = cnt[arr[i]] / col;
            int c = cnt[arr[i]] % col;
            rowCnt[r]--;
            colCnt[c]--;
            if (rowCnt[r] == 0 || colCnt[c] == 0) {
                return i;
            }
        }
        return 0;
    }
};

2662. 前往目标的最小代价

给你一个数组 start ，其中 start = [startX, startY] 表示你的初始位置位于二维空间上的 (startX, startY) 。另给你一个数组 target ，其中 target = [targetX, targetY] 表示你的目标位置 (targetX, targetY) 。

从位置 (x1, y1) 到空间中任一其他位置 (x2, y2) 的代价是 |x2 - x1| + |y2 - y1| 。

给你一个二维数组 specialRoads ，表示空间中存在的一些特殊路径。其中 specialRoads[i] = [x1i, y1i, x2i, y2i, costi] 表示第 i 条特殊路径可以从 (x1i, y1i) 到 (x2i, y2i) ，但成本等于 costi 。你可以使用每条特殊路径任意次数。

返回从 (startX, startY) 到 (targetX, targetY) 所需的最小代价。

示例 1：

输入：start = [1,1], target = [4,5], specialRoads = [[1,2,3,3,2],[3,4,4,5,1]]
输出：5
解释：从 (1,1) 到 (4,5) 的最优路径如下：
- (1,1) -> (1,2) ，移动的代价是 |1 - 1| + |2 - 1| = 1 。
- (1,2) -> (3,3) ，移动使用第一条特殊路径，代价是 2 。
- (3,3) -> (3,4) ，移动的代价是 |3 - 3| + |4 - 3| = 1.
- (3,4) -> (4,5) ，移动使用第二条特殊路径，代价是 1 。
总代价是 1 + 2 + 1 + 1 = 5 。
可以证明无法以小于 5 的代价完成从 (1,1) 到 (4,5) 。

示例 2：

输入：start = [3,2], target = [5,7], specialRoads = [[3,2,3,4,4],[3,3,5,5,5],[3,4,5,6,6]]
输出：7
解释：最优路径是不使用任何特殊路径，直接以 |5 - 3| + |7 - 2| = 7 的代价从初始位置到达目标位置。

提示：

start.length == target.length == 2
1 <= startX <= targetX <= 105
1 <= startY <= targetY <= 105
1 <= specialRoads.length <= 200
specialRoads[i].length == 5
startX <= x1i, x2i <= targetX
startY <= y1i, y2i <= targetY
1 <= costi <= 105

地址

https://leetcode.cn/contest/weekly-contest-343/problems/minimum-cost-of-a-path-with-special-roads/

题意

dijistra

思路

题目感觉出的不太好，不过解题方法还是比较简单，我们将题目中给定的 $specialRoads$ 中给定的特殊路径看做为特使的有向边 $\overrightarrow{pq}$,其中 $\overrightarrow{pq}$ 的边长为 $specialRoads[i][4]$，我们建立一个完全图，从起点 $start$ 指向所有的端点的有向边，从每个有向边的终点指向所有的所有有向边的起点，建立一个完全图，然后利用含有堆的 $dijistra$ 算法求起点到终点的最短路径即可。
复杂度分析：

时间复杂度：$O(n^2 \log n)$，其中 $n$ 为给定的特殊路径的数目。
空间复杂度：$O(n^2)$，其中 $n$ 为给定的特殊路径的数目。

代码

class Solution {
public:
    int minimumCost(vector<int>& start, vector<int>& target, vector<vector<int>>& specialRoads) {
        int n = specialRoads.size();
        int m = 2 * n + 2;
        vector<vector<pair<int, int>>> graph(m);
        vector<int> dist(m, INT_MAX);
        dist[2 * n] = 0;
        dist[2 * n + 1] = abs(start[0] - target[0]) + abs(start[1] - target[1]);
        graph[2 * n].emplace_back(2 * n + 1, abs(start[0] - target[0]) + abs(start[1] - target[1]));

        for (int i = 0; i < n; i++) {
            int cost = abs(specialRoads[i][0] - specialRoads[i][2]) + \
                       abs(specialRoads[i][1] - specialRoads[i][3]);
            graph[2 * i].emplace_back(2 * i + 1, min(cost, specialRoads[i][4]));
            for (int j = 0; j < n; j++) {
                if (i == j) continue;
                graph[2 * i + 1].emplace_back(2 * j, abs(specialRoads[i][2] - specialRoads[j][0]) + \
                                                     abs(specialRoads[i][3] - specialRoads[j][1]));
            }
            graph[2 * n].emplace_back(2 * i, abs(start[0] - specialRoads[i][0]) + \
                                             abs(start[1] - specialRoads[i][1]));
            graph[2 * n].emplace_back(2 * i + 1, abs(start[0] - specialRoads[i][2]) + \
                                                 abs(start[1] - specialRoads[i][3]));
            graph[2 * i + 1].emplace_back(2 * n + 1, abs(target[0] - specialRoads[i][2]) + \
                                                     abs(target[1] - specialRoads[i][3]));
        }

        
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.emplace(2 * n, 0);
        while (!pq.empty()) {
            auto [curr, cost] = pq.top();
            pq.pop();
            if (curr == 2 * n + 1) {
                return cost;
            }
            for (auto & [next, weight] : graph[curr]) {
                if (cost + weight < dist[next]) {
                    dist[next] = cost + weight;
                    pq.emplace(next, cost + weight);
                }
            }
        }
        return dist[2 * n + 1];
    }
};

2663. 字典序最小的美丽字符串

如果一个字符串满足以下条件，则称其为 美丽字符串 ：

它由英语小写字母表的前 k 个字母组成。
它不包含任何长度为 2 或更长的回文子字符串。

给你一个长度为 n 的美丽字符串 s 和一个正整数 k 。

请你找出并返回一个长度为 n 的美丽字符串，该字符串还满足：在字典序大于 s 的所有美丽字符串中字典序最小。如果不存在这样的字符串，则返回一个空字符串。

对于长度相同的两个字符串 a 和 b ，如果字符串 a 在与字符串 b 不同的第一个位置上的字符字典序更大，则字符串 a 的字典序大于字符串 b 。

例如，"abcd" 的字典序比 "abcc" 更大，因为在不同的第一个位置（第四个字符）上 d 的字典序大于 c 。

示例 1：

输入：s = "abcz", k = 26
输出："abda"
解释：字符串 "abda" 既是美丽字符串，又满足字典序大于 "abcz" 。
可以证明不存在字符串同时满足字典序大于 "abcz"、美丽字符串、字典序小于 "abda" 这三个条件。

示例 2：

输入：s = "dc", k = 4
输出：""
解释：可以证明，不存在既是美丽字符串，又字典序大于 "dc" 的字符串。

提示：

1 <= n == s.length <= 105
4 <= k <= 26
s 是一个美丽字符串

地址

https://leetcode.cn/contest/weekly-contest-343/problems/lexicographically-smallest-beautiful-string/

题意

贪心模拟

思路

题目看似很难，实际仔细分析一下就可以看到非常简单，我们仔细分析一下可以看到一下几点：
- 由于美丽字符的定义可以知道 $s[i] \neq s[i - 1], s[i] \neq s[i - 2]$；
- 组成长度大于 $3$ 的美丽字符串最少需要 $3$ 个字符即可，实际我们只用 $a,b,c$ 三个字符即可组成字典序最小的美丽字符串；
由于题目要求求出大于当前字符串的且字典序最小的字符串，此时根据最小字符串的定义，我们尝试从 $n-1$ 个字符依次向前遍历，并将当前的字符 $s[i]$ 替换为比当前字符 $s[i]$ 大的字符且比小于等于最大字符的字符 $a$,
- 此时 $a \in [s[i] + 1, \texttt{`a’} + k - 1]$ ，假设当前 $s[i]$ 进行了替换，且满足 $a \neq s[i-1], a \neq s[i - 2]$;
- 此时我们还需要尝试填充最小的 $s[i + 1]$,假设当前填充的字符为 $b$，此时 $b \in [\texttt{a'}, \texttt{a’} + k - 1]$，此时 $b \neq a, b \neq s[i-1]$；
- 如果我们找到合适的 $a,b$ 进行填充后，此时我们还需要用最小的字典序填充 $s[i+2, \cdots, n - 1]$, 此时根据上述的描述剩余的字符我们直接用最小的三个字符 $\texttt{a',b’,`c’}$ 依次填充即可，但是此时仍然需要满足 $s[j] \neq s[j - 1], s[j] \neq s[j - 2]$;
- 为什么 $s[i], s[i + 1]$ 不能直接用 $\texttt{a',b’,`c’}$ 填充，这是因为此时的填充关系与 $s[i -1], s[i-2]$ 有关；
复杂度分析：

时间复杂度：$O(n\times k^2)$，其中 $n$ 为字符串的长度, $k$ 为给定的数字；
空间复杂度：$O(n)$，其中 $n$ 为字符串的长度；

代码

class Solution {
public:
    string smallestBeautifulString(string s, int k) {
        int n = s.size();        
        string res;
        int replace = -1;
        for (int i = n - 1; i >= 0; i--) {
            /* 检查当前字符 */
            if (s[i] >= 'a' + k - 1) continue;
            for (int j = s[i] - 'a' + 1; j < k && replace < 0; j++) {
                /* 前一个字符相等 */
                if (i > 0 && s[i - 1] - 'a' == j) continue;
                /* 前两个字符相等 */
                if (i > 1 && s[i - 2] - 'a' == j) continue;
                if (i == n - 1) {
                    s[i] = 'a' + j;
                    return s;
                }
                for (int t = 0; t < k && replace < 0; t++) {
                    if (t == j) continue;
                    if (i > 0 && s[i - 1] == t + 'a') continue;
                    s[i] = 'a' + j;
                    s[i + 1] = 'a' + t;
                    replace = i + 1;
                }
            }
        }
        if (replace < 0) {
            return "";
        }
        for (int i = replace + 1; i < n; i++) {
            for (int j = 0; j < 3; j++) {
                if (i > 0 && s[i - 1] == 'a' + j) continue;
                if (i > 1 && s[i - 2] == 'a' + j) continue;
                s[i] = 'a' + j;
                break;
            }
        }
        return s;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 题解力扣季度赛

← leetcode biweekly contes 103 leetcode weekly contes 344 →

扫描二维码，分享此文章