leetcode biweekly contes 103
难得进入一次前 100 ,现在周赛太卷了。前三题不知道题目在出什么,数据给的太简单了,全部就是暴力即可。
6406. K 个元素的最大和
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。你需要执行以下操作 恰好 k 次,最大化你的得分:
- 从
nums中选择一个元素m。 - 将选中的元素
m从数组中删除。 - 将新元素
m + 1添加到数组中。 - 你的得分增加
m。
请你返回执行以上操作恰好 k 次后的最大得分。
示例 1:
输入:nums = [1,2,3,4,5], k = 3 |
示例 2:
输入:nums = [5,5,5], k = 2 |
提示:
1 <= nums.length <= 1001 <= nums[i] <= 1001 <= k <= 100
地址
https://leetcode.cn/contest/biweekly-contest-103/problems/maximum-sum-with-exactly-k-elements/
题意
直接模拟
思路
- 感觉太简单了,直接挑选数组中最大数字一直替换下去即可,假设原数组的最大值为 $x$,则我们将 $x$ 一直替换下去即可,显然 $x$ 替换为 $x + 1$,$x + 1$ 替换为 $x+ 2$,直到 $x + k - 1$,因此最大得分即等于 $k$ 项等差数列的和,即为 $\dfrac{k \times (2x + k - 1)}{2}$。
- 复杂度分析:
- 时间复杂度:$O(n)$。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6405. 找到两个数组的前缀公共数组
给你两个下标从 0 开始长度为 n 的整数排列 A 和 B 。
A 和 B 的 前缀公共数组 定义为数组 C ,其中 C[i] 是数组 A 和 B 到下标为 i 之前公共元素的数目。
请你返回 A 和 B 的 前缀公共数组 。
如果一个长度为 n 的数组包含 1 到 n 的元素恰好一次,我们称这个数组是一个长度为 n 的 排列 。
示例 1:
输入:A = [1,3,2,4], B = [3,1,2,4] |
示例 2:
输入:A = [2,3,1], B = [3,1,2] |
提示:
1 <= A.length == B.length == n <= 501 <= A[i], B[i] <= n- 题目保证
A和B两个数组都是n个元素的排列
地址
题意
哈希表
思路
- 简单的哈希统计即可,题目给定的数据范围只有 $50$, 让这个题目变的太简单了,明明可以做到 $10^5$ 次方数量级的数组。假设当前两个数组的前 $i-1$ 项中含有相同元素的数目为 $x$,此时 $A$ 新增了 元素 $A[i]$, 此时 $B$ 新增了 元素 $B[i]$, 此时要么相同元素的数目加 $2$ ,要么加 $1$, 要么加 $0$, 分别讨论如下:
- 假设此时 $A[i] = B[i]$, 则此时两个数组的相同元素一定增加一个为 $A[i]$;
- 假设此时 $A[i] \neq B[i]$, 则:
- 此时如果 $A[0\cdots i -1]$ 中出现过 $B[i]$, 此时相同元素的个数增加 $1$;
- 此时如果 $B[0\cdots i -1]$ 中出现过 $A[i]$, 此时相同元素的个数增加 $1$;
- 对于数组中已经出现的元素我们全部用哈希表存储,此时即可在 $O(1)$ 的时间复杂度内检测元素是否出现。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 为给定数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 为给定数组的长度。
代码
class Solution { |
6403. 网格图中鱼的最大数目
给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ,其中下标在 (r, c) 处的整数表示:
- 如果
grid[r][c] = 0,那么它是一块 陆地 。 - 如果
grid[r][c] > 0,那么它是一块 水域 ,且包含grid[r][c]条鱼。
一位渔夫可以从任意 水域 格子 (r, c) 出发,然后执行以下操作任意次:
- 捕捞格子
(r, c)处所有的鱼,或者 - 移动到相邻的 水域 格子。
请你返回渔夫最优策略下, 最多 可以捕捞多少条鱼。如果没有水域格子,请你返回 0 。
格子 (r, c) 相邻 的格子为 (r, c + 1) ,(r, c - 1) ,(r + 1, c) 和 (r - 1, c) ,前提是相邻格子在网格图内。
示例 1:
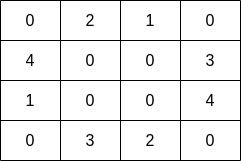
输入:grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]] |
示例 2:
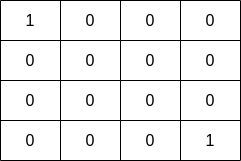
输入:grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]] |
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 100 <= grid[i][j] <= 10
地址
https://leetcode.cn/contest/biweekly-contest-103/problems/maximum-number-of-fish-in-a-grid/
题意
DFS BFS
思路
- 不晓得这个题目为啥标记为 $hard$, 本来是非常简单的题目,数据量又给的非常少,不晓得到底是怎么出题的。
- 直接遍历值大于 $0$ 的位置,并向四周扩展,即求矩阵中每个连通区域的和最大值即可,简单的 $DFS$ 或者 $BFS$ 均可。
- 复杂度分析:
- 时间复杂度:$O(mn)$,其中 $m$ 为矩阵的行数,$n$ 为矩阵的列数。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6404. 将数组清空
给你一个包含若干 互不相同 整数的数组 nums ,你需要执行以下操作 直到****数组为空 :
- 如果数组中第一个元素是当前数组中的 最小值 ,则删除它。
- 否则,将第一个元素移动到数组的 末尾 。
请你返回需要多少个操作使 nums 为空。
示例 1:
输入:nums = [3,4,-1] |
| Operation | Array |
|---|---|
| 1 | [4, -1, 3] |
| 2 | [-1, 3, 4] |
| 3 | [3, 4] |
| 4 | [4] |
| 5 | [] |
示例 2:
输入:nums = [1,2,4,3] |
| Operation | Array |
|---|---|
| 1 | [2, 4, 3] |
| 2 | [4, 3] |
| 3 | [3, 4] |
| 4 | [4] |
| 5 | [] |
示例 3:
输入:nums = [1,2,3] |
| Operation | Array |
|---|---|
| 1 | [2, 3] |
| 2 | [3] |
| 3 | [] |
提示:
1 <= nums.length <= 105-109 <= nums[i] <= 109nums中的元素 互不相同 。
地址
https://leetcode.cn/contest/biweekly-contest-103/problems/make-array-empty/
题意
线段树或者树状数组
思路
- 题目比较有意思一些,当然我们直接求肯定比较难求,但是我们可以求出每次选择最小的数并移动的步骤,然后将每次移动的步数求和即可;
- 根据题意分析,由于每个元素的值均不相同,因此我们应该按照元素的大小将所有的元素从小到大进行排序即可。假设当前的被删除的数字为原始数组中的 $nums[i]$, 下一个即将删除的元素为原始数组中 $nums[j]$, 根据题意可以知道假设当前 $nums[i]$ 移动到数组的头部,此时我们思考一下,从 $nums[i]$ 移动到 $nums[j]$ 需要多少步?实际分为下面两种情况讨论:
- 假设 $i < j$, 则此时很明显假设 $nums[i \cdots j]$ 之间没有元素被移除,则此无论数组如何变换,则从 $nums[i]$ 移动到 $nums[j]$ 需要 $j - i + 1$ 步,如果我们知道 $nums[i \cdots j]$ 之间已经被移除元素的数目为 $x$, 则此时我们可以知道从 $nums[i]$ 移动到 $nums[j]$ 需要 $j - i + 1 - x$ 步,这是因为在二者之间的 $x$ 个元素已经移除,此时我们自然想到可以用线段树或者树状数组来标记数组中每个索引位置的元素是否已经被删除,从而可以在 $O(\log n)$ 的时间复杂度内统计区间 $[i,j]$ 被删除的元素的数目。
- 假设 $i \ge j$, 则此时情况要稍微复杂一些,明显假设 $nums[j \cdots n-1],nums[0 \cdots i]$ 之间没有元素被移除,则此无论数组如何变换,则从 $nums[i]$ 移动到 $nums[j]$ 需要 $n - i + j$ 步,如果我们知道 之间已经$nums[j \cdots n-1],nums[0 \cdots i]$被移除元素的数目为 $x$, 则此时我们可以知道从 $nums[i]$ 移动到 $nums[j]$ 需要 $n - i + j - x$ 步,这是因为在二者之间的 $x$ 个元素已经移除,此时我们自然想到可以用线段树或者树状数组来标记数组中每个索引位置的元素是否已经被删除,从而可以在 $O(\log n)$ 的时间复杂度内统计两个区间 $[i,n - 1], [0,j]$ 被删除的元素的数目。
- 根据以上分析,首先我们对数组进行排序,然后按照要求对齐统计即可。
- 复杂度分析:
- 时间复杂度:$O(n \log n)$,其中 $n$ 为数组的长度;
- 空间复杂度:$O(n)$,其中 $n$ 为数组的长度;
代码
const int N = 1e5; |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
