leetcode contest 340

最近遇到难度最大的一场周赛题目了，还是比较难的题目，不过越是难的题目越是有挑战。

2614. 对角线上的质数

给你一个下标从 0 开始的二维整数数组 nums 。

返回位于 nums 至少一条 对角线 上的最大质数。如果任一对角线上均不存在质数，返回 0 。

注意：

如果某个整数大于 1 ，且不存在除 1 和自身之外的正整数因子，则认为该整数是一个质数。
如果存在整数 i ，使得 nums[i][i] = val 或者 nums[i][nums.length - i - 1]= val ，则认为整数 val 位于 nums 的一条对角线上。

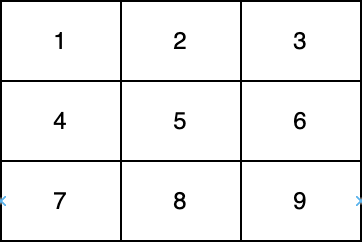
在上图中，一条对角线是 [1,5,9] ，而另一条对角线是 [3,5,7] 。

示例 1：

输入：nums = [[1,2,3],[5,6,7],[9,10,11]]
输出：11
解释：数字 1、3、6、9 和 11 是所有 "位于至少一条对角线上" 的数字。由于 11 是最大的质数，故返回 11 。

示例 2：

输入：nums = [[1,2,3],[5,17,7],[9,11,10]]
输出：17
解释：数字 1、3、9、10 和 17 是所有满足"位于至少一条对角线上"的数字。由于 17 是最大的质数，故返回 17 。

提示：

1 <= nums.length <= 300
nums.length == numsi.length
1 <= nums[i][j] <= 4*106

地址

https://leetcode.cn/contest/weekly-contest-340/problems/prime-in-diagonal/

题意

直接检测

思路

直接检测矩阵中对角线上的每个元素即可。
复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

代码

class Solution {
public:
    bool isprimer(int x) {
        if (x == 1) {
            return false;
        }
        for (int i = 2; i * i <= x; i++) {
            if (x % i == 0) {
                return false;
            }
        }
        return true;
    }
    
    int diagonalPrime(vector<vector<int>>& nums) {
        int n = nums.size();
        int res = 0;
        for (int i = 0; i < n; i++) {
            if (isprimer(nums[i][i])) {
                res = max(res, nums[i][i]);
            }
            if (isprimer(nums[i][n - 1 - i])) {
                res = max(res, nums[i][n - 1 - i]);
            }
        }
        return res;
    }
};

2615. 等值距离和

给你一个下标从 0 开始的整数数组 nums 。现有一个长度等于 nums.length 的数组 arr 。对于满足 nums[j] == nums[i] 且 j != i 的所有 j ，arr[i] 等于所有 |i - j| 之和。如果不存在这样的 j ，则令 arr[i] 等于 0 。

返回数组 arr 。

示例 1：

输入：nums = [1,3,1,1,2]
输出：[5,0,3,4,0]
解释：
i = 0 ，nums[0] == nums[2] 且 nums[0] == nums[3] 。因此，arr[0] = |0 - 2| + |0 - 3| = 5 。 
i = 1 ，arr[1] = 0 因为不存在值等于 3 的其他下标。
i = 2 ，nums[2] == nums[0] 且 nums[2] == nums[3] 。因此，arr[2] = |2 - 0| + |2 - 3| = 3 。
i = 3 ，nums[3] == nums[0] 且 nums[3] == nums[2] 。因此，arr[3] = |3 - 0| + |3 - 2| = 4 。 
i = 4 ，arr[4] = 0 因为不存在值等于 2 的其他下标。

示例 2：

输入：nums = [0,5,3]
输出：[0,0,0]
解释：因为 nums 中的元素互不相同，对于所有 i ，都有 arr[i] = 0 。

提示：

1 <= nums.length <= 105
0 <= nums[i] <= 109

地址

https://leetcode.cn/contest/weekly-contest-340/problems/sum-of-distances/

题意

直接枚举

思路

利用哈希表将相同的元素进行分组，分组完成后直接按照要求分组中所有的元素对某个元素的绝对值差的和即可。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 为数组的长度。
空间复杂度：$O(n)$。其中 $n$ 为数组的长度。

代码

class Solution {
public:
    vector<long long> distance(vector<int>& nums) {
        unordered_map<int, vector<long long>> cnt;
        unordered_map<int, vector<long long>> prefix;
        for (int i = 0; i < nums.size(); i++) {
            cnt[nums[i]].emplace_back(i);
        }
        
        int n = nums.size();
        vector<long long> res(n);
        for (auto [_, vec] : cnt) {
            sort(vec.begin(), vec.end());
            long long tot = accumulate(vec.begin(), vec.end(), 0LL);
            long long prev = 0;
            int m = vec.size();
            for (int i = 0; i < vec.size(); i++) {
                res[vec[i]] = tot - (long long)(m - i) * vec[i] + (long long)i * vec[i] - prev;
                tot -= vec[i];
                prev += vec[i];
            }
        }
        return res;
    }
};

2616. 最小化数对的最大差值

给你一个下标从 0 开始的整数数组 nums 和一个整数 p 。请你从 nums 中找到 p 个下标对，每个下标对对应数值取差值，你需要使得这 p 个差值的 最大值 最小。同时，你需要确保每个下标在这 p 个下标对中最多出现一次。

对于一个下标对 i 和 j ，这一对的差值为 |nums[i] - nums[j]| ，其中 |x| 表示 x 的 绝对值 。

请你返回 p 个下标对对应数值 最大差值 的 最小值 。

示例 1：

输入：nums = [10,1,2,7,1,3], p = 2
输出：1
解释：第一个下标对选择 1 和 4 ，第二个下标对选择 2 和 5 。
最大差值为 max(|nums[1] - nums[4]|, |nums[2] - nums[5]|) = max(0, 1) = 1 。所以我们返回 1 。

示例 2：

输入：nums = [4,2,1,2], p = 1
输出：0
解释：选择下标 1 和 3 构成下标对。差值为 |2 - 2| = 0 ，这是最大差值的最小值。

提示：

1 <= nums.length <= 105
0 <= nums[i] <= 109
0 <= p <= (nums.length)/2

地址

https://leetcode.cn/contest/weekly-contest-340/problems/minimize-the-maximum-difference-of-pairs/

题意

二分查找

思路

根据题目可以知道，一般遇到最大值的最小值，或者最小值的最大值，此时就需要用到二分查找；
我们需要观察一些特征:

如果可以选 $\textit{nums}[0]$ 和 $\textit{nums}[1]$，那么答案等于「n−2 个数的最多数对个数」+1。
如果不选 $\textit{nums}[0]$，那么答案等于「n−1个数的最多数对个数」。
这两种情况取最大值。

复杂度分析：

时间复杂度：$O(n \log U)$，其中 $n$ 为数组的长度。
空间复杂度：$O(1)$。

代码

class Solution {
public:
    int minimizeMax(vector<int>& nums, int p) {
        sort(nums.begin(), nums.end());
        int l = 0;
        int r = 1e9 + 7;
        int res = 0;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            int tot = 0;
            int i = 1;
            while (i < nums.size()) {
                if (nums[i] - nums[i - 1] <= mid) {
                    tot++;
                    i += 2;
                } else {
                    i++;
                }
            }
            if (tot >= p) {
                res = mid;
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
        return res;
    }
};

2617. 网格图中最少访问的格子数

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。

当你在格子 (i, j) 的时候，你可以移动到以下格子之一：

满足 j < k <= grid[i][j] + j 的格子 (i, k) （向右移动），或者
满足 i < k <= grid[i][j] + i 的格子 (k, j) （向下移动）。

请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数，如果无法到达右下角格子，请你返回 -1 。

示例 1：

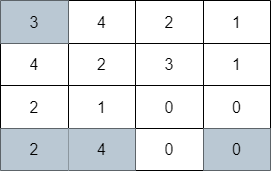
输入：grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
输出：4
解释：上图展示了到达右下角格子经过的 4 个格子。

示例 2：

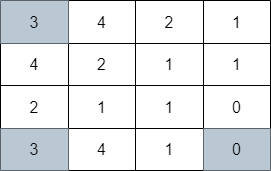
输入：grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
输出：3
解释：上图展示了到达右下角格子经过的 3 个格子。

示例 3：

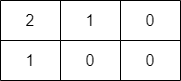
输入：grid = [[2,1,0],[1,0,0]]
输出：-1
解释：无法到达右下角格子。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
0 <= grid[i][j] < m * n
grid[m - 1][n - 1] == 0

地址

https://leetcode.cn/contest/weekly-contest-340/problems/minimum-number-of-visited-cells-in-a-grid/

题意

BFS

思路

本题本质也是一个大号的跳跃游戏，因此我们可以参考 339 周 T4 的题解来做这道题目。用 treeset 存储每行和每列中未访问过的元素，假设当前方位的坐标为 $(x,y)$，此时我们操作如下:

在 $x$ 行中的元素找到属于区间 $[x * col + y, x * col + y + grid[x][y]]$ 的元素，此时我们直接将处于该区间的元素删除即可，同时也要在对应的列中删除未访问的元素；
在 $y$ 列中的元素找到属于区间 $[x * col + y, (x + grid[x][y])* col + y]$ 的元素，此时我们直接将处于该区间的元素删除即可，同时也要在对应的行中删除未访问的元素；
此时我们可以很快的利用二分查找即可找到区间的起点，然后依次从区间的起点开始遍历，边遍历边删除即可；

我们按照层次遍历的方式依次对当前可以访问的元素进行访问，直到到达终点即可。
复杂度分析：

时间复杂度：$O(m \times n \times(\log m + \log n))$，其中 $m$ 为节点的数目,$m$ 表示查询的次数。
空间复杂度：$O(m \times n)$，其中 $m$ 为节点的数目,$m$ 表示查询的次数。

代码

class Solution {
public:
    int minimumVisitedCells(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<set<int>> rowCnt(m);
        vector<set<int>> colCnt(n);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                rowCnt[i].emplace(i * n + j);
                colCnt[j].emplace(i * n + j);
            }
        }

        queue<int> qu;
        qu.emplace(0);
        int step = 0;
        while (!qu.empty()) {
            int sz = qu.size();
            for (int i = 0; i < sz; i++) {
                int curr = qu.front();
                qu.pop();
                if (curr == m * n - 1) {
                    return step + 1;
                }
                int x = curr / n;
                int y = curr % n;
                if (grid[x][y] == 0) {
                    rowCnt[x].erase(curr);
                    colCnt[y].erase(curr);
                    continue;
                }
                /* 向右移动 */
                for (auto it = rowCnt[x].upper_bound(curr); it != rowCnt[x].end() && (*it) - curr <= grid[x][y]; it = rowCnt[x].erase(it)) {
                    qu.emplace(*it);
                    colCnt[y].erase(*it);
                }
                /* 向下移动 */
                for (auto it = colCnt[y].upper_bound(curr); it != colCnt[y].end() && ((*it) - curr) / n <= grid[x][y]; it = colCnt[y].erase(it)) {
                    qu.emplace(*it);
                    rowCnt[x].erase(*it);
                }
            }
            step++;
        }
        return -1;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 力扣周赛题解

← leetcode contest 341 leetcode contest 342 →

扫描二维码，分享此文章