leetcode biweekly contest 101

第四题比较有意思的题目，希望多多来点有意思的题目，模板题目太多了。

6354. K 件物品的最大和

袋子中装有一些物品，每个物品上都标记着数字 1 、0 或 -1 。

给你四个非负整数 numOnes 、numZeros 、numNegOnes 和 k 。

袋子最初包含：

numOnes 件标记为 1 的物品。
numZeroes 件标记为 0 的物品。
numNegOnes 件标记为 -1 的物品。

现计划从这些物品中恰好选出 k 件物品。返回所有可行方案中，物品上所标记数字之和的最大值。

示例 1：

输入：numOnes = 3, numZeros = 2, numNegOnes = 0, k = 2
输出：2
解释：袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 2 件标记为 1 的物品，得到的数字之和为 2 。
可以证明 2 是所有可行方案中的最大值。

示例 2：

输入：numOnes = 3, numZeros = 2, numNegOnes = 0, k = 4
输出：3
解释：袋子中的物品分别标记为 {1, 1, 1, 0, 0} 。取 3 件标记为 1 的物品，1 件标记为 0 的物品，得到的数字之和为 3 。
可以证明 3 是所有可行方案中的最大值。

提示：

0 <= numOnes, numZeros, numNegOnes <= 50
0 <= k <= numOnes + numZeros + numNegOnes

地址

https://leetcode.cn/contest/weekly-contest-338/problems/k-items-with-the-maximum-sum/

题意

直接模拟

思路

直接模拟即可，我们知道最小的数字要么为一位，要么为两位；
- 如果两个数组含有相同的数字，则直接返回相同数字中的最小一位即可；
- 如果两个数组中不含有相同的数字，则此时我们需要从数组 $1$ 中选择最小一位，同时从数组 $2$ 中选择最小的一位，然后二者构成最小的数字即可；
复杂度分析：

时间复杂度：$O(n^2)$。实际可以优化到 $n\log n$。
空间复杂度：$O(n)$。

代码

class Solution {
public:
    int minNumber(vector<int>& nums1, vector<int>& nums2) {
        vector<int> cnt;
        for (auto x : nums1) {
            for (auto y : nums2) {
                if (x == y) {
                    cnt.emplace_back(x);
                }
            }
        }
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        sort(cnt.begin(), cnt.end());
        if (cnt.size() > 0) {
            return cnt[0];
        } else {
            return nums1[0] > nums2[0] ? (nums2[0] * 10 + nums1[0]) : (nums1[0] * 10 + nums2[0]);
        }
    }
};

2606. 找到最大开销的子字符串

给你一个字符串 s ，一个字符 互不相同 的字符串 chars 和一个长度与 chars 相同的整数数组 vals 。

子字符串的开销 是一个子字符串中所有字符对应价值之和。空字符串的开销是 0 。

字符的价值 定义如下：

如果字符不在字符串 chars中，那么它的价值是它在字母表中的位置（下标从1 开始）。
- 比方说，'a' 的价值为 1 ，'b' 的价值为 2 ，以此类推，'z' 的价值为 26 。
否则，如果这个字符在 chars 中的位置为 i ，那么它的价值就是 vals[i] 。

请你返回字符串 s 的所有子字符串中的最大开销。

示例 1：

输入：s = "adaa", chars = "d", vals = [-1000]
输出：2
解释：字符 "a" 和 "d" 的价值分别为 1 和 -1000 。
最大开销子字符串是 "aa" ，它的开销为 1 + 1 = 2 。
2 是最大开销。

示例 2：

输入：s = "abc", chars = "abc", vals = [-1,-1,-1]
输出：0
解释：字符 "a" ，"b" 和 "c" 的价值分别为 -1 ，-1 和 -1 。
最大开销子字符串是 "" ，它的开销为 0 。
0 是最大开销。

提示：

1 <= s.length <= 105
s 只包含小写英文字母。
1 <= chars.length <= 26
chars 只包含小写英文字母，且 互不相同 。
vals.length == chars.length
-1000 <= vals[i] <= 1000

地址

https://leetcode.cn/contest/biweekly-contest-101/problems/find-the-substring-with-maximum-cost/

题意

前缀和

思路

题目为简单的贪心法则，由于只能计算连续的字符串的开销，因此我们计算当前从 $0$ 开始到 $i$ 的开销，即 $s[0\cdots i]$ 的开销，每次找到 $s[0\cdots j],j < k$ 的最小值，用当前值减去最小值即可找到以 $i$ 为结尾的连续子字符串的最大开销；
复杂度分析：

时间复杂度：$O(n \log n)$，其中 $n$ 为字符串的长度。
空间复杂度：$O(n)$，其中 $n$ 为字符串的长度。

代码

class Solution {
public:
    int maximumCostSubstring(string s, string chars, vector<int>& vals) {
        vector<int> cnt(26);
        for (int i = 0; i < 26; i++) {
            cnt[i] = i + 1;
        }
        for (int i = 0; i < chars.size(); i++) {
            cnt[chars[i] - 'a'] = vals[i];
        }
        set<int> sum;
        sum.emplace(0);
        int curr = 0;
        int ans = 0;
        for (auto c : s) {
            curr += cnt[c - 'a'];
            ans = max(ans, curr - *sum.begin());
            sum.emplace(curr);
        }
        return ans;
    }
};

2607. 使子数组元素和相等

给你一个下标从 0 开始的整数数组 arr 和一个整数 k 。数组 arr 是一个循环数组。换句话说，数组中的最后一个元素的下一个元素是数组中的第一个元素，数组中第一个元素的前一个元素是数组中的最后一个元素。

你可以执行下述运算任意次：

选中 arr 中任意一个元素，并使其值加上 1 或减去 1 。

执行运算使每个长度为 k 的 子数组 的元素总和都相等，返回所需要的最少运算次数。

子数组 是数组的一个连续部分。

示例 1：

输入：arr = [1,4,1,3], k = 2
输出：1
解释：在下标为 1 的元素那里执行一次运算，使其等于 3 。
执行运算后，数组变为 [1,3,1,3] 。
- 0 处起始的子数组为 [1, 3] ，元素总和为 4 
- 1 处起始的子数组为 [3, 1] ，元素总和为 4 
- 2 处起始的子数组为 [1, 3] ，元素总和为 4 
- 3 处起始的子数组为 [3, 1] ，元素总和为 4

示例 2：

输入：arr = [2,5,5,7], k = 3
输出：5
解释：在下标为 0 的元素那里执行三次运算，使其等于 5 。在下标为 3 的元素那里执行两次运算，使其等于 5 。
执行运算后，数组变为 [5,5,5,5] 。
- 0 处起始的子数组为 [5, 5, 5] ，元素总和为 15
- 1 处起始的子数组为 [5, 5, 5] ，元素总和为 15
- 2 处起始的子数组为 [5, 5, 5] ，元素总和为 15
- 3 处起始的子数组为 [5, 5, 5] ，元素总和为 15

提示：

1 <= k <= arr.length <= 105
1 <= arr[i] <= 109

地址

https://leetcode.cn/contest/biweekly-contest-101/problems/make-k-subarray-sums-equal/

题意

中位数

思路

首先我们需要将数组进行分类筛选，若使得长度为 $k$ 子数组和相等，根据公式可以知道：

$$ \sum_{j=i}^{j+k-1}arr[j] = \sum_{i=i+1}^{j+k}arr[j]$$

由上述公式可以推出 $arr[i] = arr[(i + k) \mod n]$;
我们只需要满足所有的 $arr[i] = arr[(i + k) \mod n]$，则一定可以使得所有长度为 $k$ 的连续子数组相等，因此题目变成了使得$arr[i] = arr[(i + k) \mod n]$ 相等的最少运算次数，此时题目就变得很简单了。
首先我们按照上述规则对需要相等的元素进行分类，此时我们可以模仿欧拉素数筛选法，很快即可对数组中的元素进行分类；再次思考一个经典问题，如何使得数组中元素相等的最小操作，实际是将数组中的元素全部变为当前数组的中位数时所需的操作数最小，此时我们直接求出所有元素与中位数的差的绝对值之和即可。
复杂度分析：

时间复杂度：$O(n \log n)$，其中 $n$ 为数组的长度。
空间复杂度：$O(n)$，其中 $n$ 为数组的长度。

代码

class Solution {
public:
    long long makeSubKSumEqual(vector<int>& arr, int k) {
        int n = arr.size();
        vector<bool> visit(n, false);
        vector<vector<int>> cnt;
        for (int i = 0; i < n; i++) {
            if (!visit[i]) {
                vector<int> curr;
                for (int j = i; visit[j] != true; j = (j + k) % n) {
                    curr.emplace_back(arr[j]);
                    visit[j] = true;
                }
                sort(curr.begin(), curr.end());
                cnt.emplace_back(curr);
            }
        }
        long long res = 0;
        for (int i = 0; i < cnt.size(); i++) {
            long long sum = accumulate(cnt[i].begin(), cnt[i].end(), 0LL);
            long long mid = 0;
            int m = cnt[i].size();
            if (m % 2 == 0) {
                mid = ((long long)cnt[i][m / 2 - 1] + cnt[i][m / 2]) / 2;
            } else {
                mid = cnt[i][m / 2];
            }
            for (auto v : cnt[i]) {
                res += abs(v - mid);
            }
        }
        return res;
    }
};

2608. 图中的最短环

现有一个含 n 个顶点的双向图，每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接，并且不存在与自身相连的顶点。

返回图中最短环的长度。如果不存在环，则返回 -1 。

环是指以同一节点开始和结束，并且路径中的每条边仅使用一次。

示例 1：

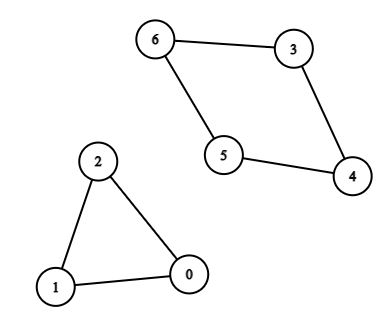
输入：n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
输出：3
解释：长度最小的循环是：0 -> 1 -> 2 -> 0

示例 2：

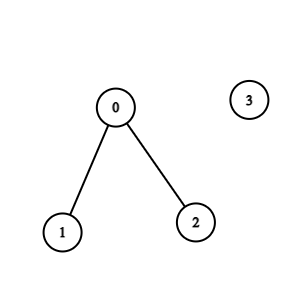
输入：n = 4, edges = [[0,1],[0,2]]
输出：-1
解释：图中不存在循环

提示：

2 <= n <= 1000
1 <= edges.length <= 1000
edges[i].length == 2
0 <= ui, vi < n
ui != vi
不存在重复的边

地址

https://leetcode.cn/contest/biweekly-contest-101/problems/shortest-cycle-in-a-graph/

题意

广度优先搜索

思路

题目比较有意思，一开始我还想着是不是需要弄 tarjan 找连通单元，后来发现不需要，直接枚举每点为起点，找到该点为起点的最小环即可。
找到环需要一点技巧，以 $i$ 为起点找到所有点到达 $i$ 的最小距离，如果发现存在环则记录环的大小即可，即对于同一个点，存在两条不同的路径到达该点时，即存在环，我们使用 bfs 即可，此时可以模仿 dfs 记录父亲节点，放置出现重复。
看到有人还有另外一种做法，即删除边的做法，每次删除边 $(i,j)$ 后，如果任然存在 $i$ 到 $j$ 的路径，则表示 $i$ 到 $j$ 之间一定存在环，这个解法非常容易理解，也比较好写，推荐该解法。
复杂度分析：

时间复杂度：$O(n^2)$，其中$ n$ 表示节点的数目。
空间复杂度：$O(n+m)$，其中$ n$ 表示节点的数目，$m$ 表示边数。

代码

删除点

class Solution {
public:
    int findShortestCycle(int n, vector<vector<int>>& edges) {
        vector<vector<int>> graph(n);
        for (auto e : edges) {
            graph[e[0]].emplace_back(e[1]);
            graph[e[1]].emplace_back(e[0]);
        }
        
        int res = INT_MAX;
        for (int i = 0; i < n; i++) {
            vector<int> dis(n, -1);
            queue<pair<int, int>> qu;
            qu.emplace(-1, i);
            dis[i] = 0;
            int cycleSize = INT_MAX;
            while (!qu.empty()) {
                auto [prev, curr] = qu.front();
                qu.pop();
                for (auto v : graph[curr]) {
                    if (v == prev) continue;
                    if (dis[v] < 0) {
                        qu.emplace(curr, v);
                        dis[v] = dis[curr] + 1;
                    } else {
                        cycleSize = min(cycleSize, dis[curr] + dis[v] + 1);
                    }
                }
            }
            res = min(res, cycleSize);
        }
        return res == INT_MAX ? -1 : res;
    }
};

删除边

class Solution {
public:
    int findShortestCycle(int n, vector<vector<int>>& edges) {
        vector<vector<int>> graph(n);
        for (auto e : edges) {
            graph[e[0]].emplace_back(e[1]);
            graph[e[1]].emplace_back(e[0]);
        }
        
        int res = INT_MAX;
        for (int i = 0; i < n; i++) {
            for (auto j : graph[i]) {
                vector<int>dis(n, -1);
                queue<int> qu;
                qu.emplace(i);
                dis[i] = 0;
                while (!qu.empty()) {
                    int curr = qu.front();
                    qu.pop();
                    for (auto v : graph[curr]) {
                        if (dis[v] >= 0) continue;
                        if (curr == i && v == j) continue;
                        qu.emplace(v);
                        dis[v] = dis[curr] + 1;
                    }
                }
                if (dis[j] >= 0) {
                    res = min(res, dis[j] + 1);
                }
            }
        }
        
        if (res == INT_MAX) return -1;
        return res;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 力扣周赛题解

← leetcode weekly contest 338 leetcode biweekly contest 102 →

扫描二维码，分享此文章