leetcode weekly contest 337

周赛的题目被大家骂了一遍，果真不咋样，特别是第二题，题目坑。

2595. 奇偶位数

给你一个正整数 n 。

用 even 表示在 n 的二进制形式（下标从 0 开始）中值为 1 的偶数下标的个数。

用 odd 表示在 n 的二进制形式（下标从 0 开始）中值为 1 的奇数下标的个数。

返回整数数组 answer ，其中 answer = [even, odd] 。

示例 1：

输入：n = 17
输出：[2,0]
解释：17 的二进制形式是 10001 。 
下标 0 和 下标 4 对应的值为 1 。 
共有 2 个偶数下标，0 个奇数下标。

示例 2：

输入：n = 2
输出：[0,1]
解释：2 的二进制形式是 10 。 
下标 1 对应的值为 1 。 
共有 0 个偶数下标，1 个奇数下标。

提示：

1 <= n <= 1000

地址

https://leetcode.cn/contest/weekly-contest-337/problems/number-of-even-and-odd-bits/

题意

直接模拟

思路

直接模拟即可，统计偶数下标与奇数下标的数目即可。
复杂度分析：

时间复杂度：$O(\log n)$。
空间复杂度：$O(\log n)$。

代码

class Solution {
public:
    vector<int> evenOddBit(int n) {
        vector<int> bits;
        while (n != 0) {
            bits.emplace_back(n & 1);
            n >>= 1;
        }
        vector<int> ans(2);
        for (int i = 0; i < bits.size(); i += 2) {
            ans[0] += bits[i];
        }
        for (int i = 1; i < bits.size(); i += 2) {
            ans[1] += bits[i];
        }
        return ans;
    }
};

2596. 检查骑士巡视方案

骑士在一张 n x n 的棋盘上巡视。在有效的巡视方案中，骑士会从棋盘的 左上角 出发，并且访问棋盘上的每个格子 恰好一次 。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

示例 1：

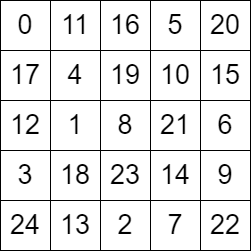
输入：grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
输出：true
解释：grid 如上图所示，可以证明这是一个有效的巡视方案。

示例 2：

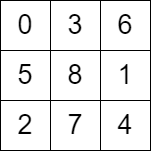
输入：grid = [[0,3,6],[5,8,1],[2,7,4]]
输出：false
解释：grid 如上图所示，考虑到骑士第 7 次行动后的位置，第 8 次行动是无效的。

提示：

n == grid.length == grid[i].length
3 <= n <= 7
0 <= grid[row][col] < n * n
grid 中的所有整数 互不相同

地址

https://leetcode.cn/contest/weekly-contest-336/problems/rearrange-array-to-maximize-prefix-score/

题意

排序 + 模拟

思路

好好的题目被出的太差了，直接按照单元格的大小进行排序，然后依次检测相邻的单元格是否满足要求。
$$
|x_i - x_{i+1} = 2| \And |y_i - y_{i+1} = 1| \tag{1} \
$$
$$
|x_i - x_{i+1} = 1| \And |y_i - y_{i+1} = 2| \tag{2} \
$$
满足上述两种的一种即可满足跳跃条件
复杂度分析：

时间复杂度：$O(n^2 \log n)$，其中 $n$ 为棋盘的长度。
空间复杂度：$O(\log n)$，其中 $n$ 为棋盘的长度。排序需要的空间为 $O(\log n)$。

代码

class Solution {
public:
    bool checkValidGrid(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<pair<int, int>> arr;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                arr.emplace_back(i, j);
            }
        }
        sort(arr.begin(), arr.end(), [&](pair<int, int> &a, pair<int, int> &b) {
            return grid[a.first][a.second] < grid[b.first][b.second];
        });
        if (arr[0].first != 0 || arr[0].second != 0) {
            return false;
        }
        for (int i = 1; i < arr.size(); i++) {
            int dx = abs(arr[i - 1].first - arr[i].first);
            int dy = abs(arr[i - 1].second - arr[i].second);
            if (!((dx == 1 && dy == 2) || (dx == 2 && dy == 1))) {
                return false;
            }
        }
        return true;
    }
};

2597. 美丽子集的数目

给你一个由正整数组成的数组 nums 和一个正整数 k 。

如果 nums 的子集中，任意两个整数的绝对差均不等于 k ，则认为该子数组是一个美丽子集。

返回数组 nums 中非空且美丽的子集数目。

nums 的子集定义为：可以经由 nums 删除某些元素（也可能不删除）得到的一个数组。只有在删除元素时选择的索引不同的情况下，两个子集才会被视作是不同的子集。

示例 1：

输入：nums = [2,4,6], k = 2
输出：4
解释：数组 nums 中的美丽子集有：[2], [4], [6], [2, 6] 。
可以证明数组 [2,4,6] 中只存在 4 个美丽子集。

示例 2：

输入：nums = [1], k = 1
输出：1
解释：数组 nums 中的美丽数组有：[1] 。
可以证明数组 [1] 中只存在 1 个美丽子集。

提示：

1 <= nums.length <= 20
1 <= nums[i], k <= 1000

地址

https://leetcode.cn/contest/weekly-contest-336/problems/count-the-number-of-beautiful-subarrays/

题意

记忆化搜索

思路

看到题目基本上可以直接用状态压缩，但是 $n \times 2^n$ 的时间复杂度会超时，提前预处理然后用记忆化搜索可以优化到 $2^n$ 即可。
- 提前预处理 $nums[i]$ 与哪些数不能在一个子集中，可以用一个二进制掩码 $mask$ 表示；
- 假设当前 $i-1$ 元素中取出的数为 $state$, 如果 $state$ 与 $mask[i]$ 存在交集则说明当前已经取出的子集中不能包含 $nums[i]$, 此时我们需要遍历下一个元素。
更加简介的 $O(n)$ 的做法：我们对所有的数进行分组，仅仅考虑与 $k$ 取模相同的分组，如果两个数对 $k$ 取模的结果不相同，则两个数相减的绝对值一定不等于 $k$，因此我们可以考虑按照取模的结果进行分组，分组之后我们仅仅考虑分组内的数目的互斥原理，此时我们可以参考 198. 打家劫舍的经典的动态规划的做法，题目就变的简单许多。不同的子集之间互为相乘。
复杂度分析：

时间复杂度：$O(n^2 + 2^n)$，其中 $n$ 为数组的长度。
空间复杂度：$O(n)$，其中 $n$ 为数组的长度。

代码

class Solution {
public:
    int beautifulSubsets(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> dp(n);
        for (int i = 0; i < n; i++) {
            int mask = 0;
            for (int j = 0; j < n; j++) {
                if (abs(nums[j] - nums[i]) == k) {
                    mask |= (1 << j);
                }
            }
            dp[i] = mask;
        }
        vector<int> memo(1 << n, -1);
        function<int(int, int)> dfs = [&](int pos, int mask) ->int {
            if (memo[mask] != -1) {
                return memo[mask];
            }
            if (pos == n)  {
                return 1;
            }
            int ret = 0;
            ret = dfs(pos + 1, mask);
            if ((mask & dp[pos]) == 0) {
                ret += dfs(pos + 1, mask | (1 << pos));
            }
            memo[mask] = ret;
            return ret;
        };
        return dfs(0, 0) - 1;
    }
};

class Solution {
public:
    int beautifulSubsets(vector<int>& nums, int k) {
        int n = nums.size();
        vector<map<int, int>> cnt(k);
        for (auto v : nums) {
            cnt[v % k][v]++;
        }
        int ans = 1;
        for (int i = 0; i < k; i++) {
            if (cnt[i].size() == 0) continue;
            int m = cnt[i].size();
            vector<int> dp(m + 1, 1);
            int j = 1;
            for (auto it = cnt[i].begin(); it != cnt[i].end(); it++, j++) {
                if (j == 1) {
                    dp[j] = 1 << it->second;
                } else {
                    if (it->first - prev(it)->first == k) {
                        dp[j] = dp[j - 1] + dp[j - 2] * ((1 << it->second) - 1);
                    } else {
                        dp[j] = dp[j - 1] * (1 << it->second);
                    }
                }
            }
            ans = ans * dp[m];
        }
        return ans - 1;
    }
};

2598. 执行操作后的最大 MEX

给你一个下标从 0 开始的整数数组 nums 和一个整数 value 。

在一步操作中，你可以对 nums 中的任一元素加上或减去 value 。

例如，如果 nums = [1,2,3] 且 value = 2 ，你可以选择 nums[0] 减去 value ，得到 nums = [-1,2,3] 。

数组的 MEX (minimum excluded) 是指其中数组中缺失的最小非负整数。

例如，[-1,2,3] 的 MEX 是 0 ，而 [1,0,3] 的 MEX 是 2 。

返回在执行上述操作 任意次 后，nums 的最大 MEX 。

示例 1：

输入：nums = [1,-10,7,13,6,8], value = 5
输出：4
解释：执行下述操作可以得到这一结果：
- nums[1] 加上 value 两次，nums = [1,0,7,13,6,8]
- nums[2] 减去 value 一次，nums = [1,0,2,13,6,8]
- nums[3] 减去 value 两次，nums = [1,0,2,3,6,8]
nums 的 MEX 是 4 。可以证明 4 是可以取到的最大 MEX 。

示例 2：

输入：nums = [1,-10,7,13,6,8], value = 7
输出：2
解释：执行下述操作可以得到这一结果：
- nums[2] 减去 value 一次，nums = [1,-10,0,13,6,8]
nums 的 MEX 是 2 。可以证明 2 是可以取到的最大 MEX 。

提示：

1 <= nums.length, value <= 105
-109 <= nums[i] <= 109

地址

https://leetcode.cn/contest/weekly-contest-337/problems/smallest-missing-non-negative-integer-after-operations/

题意

贪心

思路

感觉算是简单题目吧，我们知道对于 $x$ 无论如何变化，其只能变换为 $x \mod value + a \times value$ , 由于其只能在该区间中取值，因此我们可以对其取 $value$模，即得到最小的正整数，然后我们依次从小到大排列即可得到最大 $MEX$。从 $0$ 开始试探，直到无法满足题目要求即可。
复杂度分析：

时间复杂度：$O(n)$，其中$ n$ 表示数组的长度。
空间复杂度：$O(value)$。

代码

class Solution {
public:
    int findSmallestInteger(vector<int>& nums, int value) {
        int n = nums.size();
        unordered_map<int, int> cnt;
        for (auto v : nums) {
            cnt[(v % value + value) % value]++;
        }
        for (int i = 0;;i++) {
            int x = i % value;
            if (cnt.count(x)) {
                cnt[x]--;
                if (cnt[x] == 0) {
                    cnt.erase(x);
                }
            } else {
                return i;
            }
        }
        return 0;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 力扣周赛题解

← leetcode biweekly contest 100 【2023】新年计划 →

扫描二维码，分享此文章