且听疯吟

leetcode weekly contest 335

2023-03-05

leetcode weekly contest 335

本场周赛的题目的第三题确实比较好的题目，难得见到高质量的第三题。

6307. 递枕头

n 个人站成一排，按从 1 到 n 编号。

最初，排在队首的第一个人拿着一个枕头。每秒钟，拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾，传递方向就会改变，队伍会继续沿相反方向传递枕头。

  • 例如，当枕头到达第 n 个人时，TA 会将枕头传递给第 n - 1 个人，然后传递给第 n - 2 个人，依此类推。

给你两个正整数 n 和 time ，返回 time 秒后拿着枕头的人的编号。

示例 1：

输入：n = 4, time = 5
输出：2
解释：队伍中枕头的传递情况为：1 -> 2 -> 3 -> 4 -> 3 -> 2 。
5 秒后，枕头传递到第 2 个人手中。

示例 2：

输入：n = 3, time = 2
输出：3
解释：队伍中枕头的传递情况为：1 -> 2 -> 3 。
2 秒后，枕头传递到第 3 个人手中。

提示：

  • 2 <= n <= 1000
  • 1 <= time <= 1000

地址

https://leetcode.cn/contest/weekly-contest-335/problems/pass-the-pillow/

题意

找规律即可

思路

  1. 每次来回需要花费的时间为 $2*(n - 1)$，我们对 $2*(n - 1)$ 进行取模：
  • 如果余数大于 $n - 1$，此时需要的位置为 $2 * n - x - 1$;
  • 如果余数小于等于 $n - 1$，此时需要的位置为 $1 + x$;
  1. 复杂度分析：
  • 时间复杂度：$O(1)$。
  • 空间复杂度：$O(1)$。

代码

class Solution {
public:
    int passThePillow(int n, int time) {
        int x = time % (2 * ( n - 1));
        if (x <= n - 1) {
            return 1 + x;
        } else {
            return 2 * n - x - 1;
        }
    }
};

6308. 二叉树中的第 K 大层和

给你一棵二叉树的根节点 root 和一个正整数 k 。

树中的 层和 是指 同一层 上节点值的总和。

返回树中第 k 大的层和（不一定不同）。如果树少于 k 层，则返回 -1 。

注意，如果两个节点与根节点的距离相同，则认为它们在同一层。

示例 1：

img

输入：root = [5,8,9,2,1,3,7,4,6], k = 2
输出：13
解释：树中每一层的层和分别是：
- Level 1: 5
- Level 2: 8 + 9 = 17
- Level 3: 2 + 1 + 3 + 7 = 13
- Level 4: 4 + 6 = 10
第 2 大的层和等于 13 。

示例 2：

img

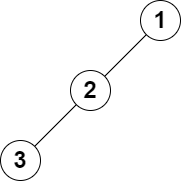
输入：root = [1,2,null,3], k = 1
输出：3
解释：最大的层和是 3 。

提示：

  • 树中的节点数为 n
  • 2 <= n <= 105
  • 1 <= Node.val <= 106
  • 1 <= k <= n

地址

https://leetcode.cn/contest/weekly-contest-335/problems/kth-largest-sum-in-a-binary-tree/

题意

层次遍历

思路

  1. 直接利用 $BFS$ 将二叉树中所有层次的和求出来，然后将其排序取最大的第 $k$ 的数即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 为二叉树节点的数目。
  • 空间复杂度：$O(n)$，其中 $n$ 为二叉树节点的数目。

代码

class Solution {
public:
    long long kthLargestLevelSum(TreeNode* root, int k) {
        vector<long long> arr;
        queue<TreeNode *> qu;
        qu.emplace(root);
        while (!qu.empty()) {
            int sz = qu.size();
            long long curr = 0;
            for (int i = 0; i < sz; i++) {
                TreeNode * node = qu.front();
                qu.pop();
                curr += node->val;
                if (node->left) {
                    qu.emplace(node->left);
                }
                if (node->right) {
                    qu.emplace(node->right);
                }
            }
            arr.emplace_back(curr);
        }
        sort(arr.begin(), arr.end(), [&](long long a, long long b) {
            return a > b;
        });
        if (arr.size() < k) {
            return -1;
        }
        return arr[k - 1];
    }
};

6309. 分割数组使乘积互质

给你一个长度为 n 的整数数组 nums ，下标从 0 开始。

如果在下标 i 处 分割 数组，其中 0 <= i <= n - 2 ，使前 i + 1 个元素的乘积和剩余元素的乘积互质，则认为该分割 有效 。

  • 例如，如果 nums = [2, 3, 3] ，那么在下标 i = 0 处的分割有效，因为 2 和 9 互质，而在下标 i = 1 处的分割无效，因为 6 和 3 不互质。在下标 i = 2 处的分割也无效，因为 i == n - 1 。

返回可以有效分割数组的最小下标 i ，如果不存在有效分割，则返回 -1 。

当且仅当 gcd(val1, val2) == 1 成立时，val1 和 val2 这两个值才是互质的，其中 gcd(val1, val2) 表示 val1 和 val2 的最大公约数。

示例 1：

img

输入：nums = [4,7,8,15,3,5]
输出：2
解释：上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
唯一一个有效分割位于下标 2 。

示例 2：

img

输入：nums = [4,7,15,8,3,5]
输出：-1
解释：上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
不存在有效分割。

提示：

  • n == nums.length
  • 1 <= n <= 104
  • 1 <= nums[i] <= 106

地址

https://leetcode.cn/contest/weekly-contest-335/problems/split-the-array-to-make-coprime-products/

题意

质数区+间合并

思路

  1. 对每个元素的质因子分解，并求出所有的含有质因子 $x$ 覆盖的最大区间为 $[start, end]$，这表示区间 $[start,end]$ 在划分时一定要划分到一起，要么全部划分到左边，要么全部划分到右边，我们在筛选时没有必要筛选 $[2,U]$，实际我们只需要筛选 $[2,\sqrt{U}]$ 即可，将 $[2,\sqrt{U}]$ 筛选完成后，剩下的数必然为质数。
  2. 我们假设质数 $a$ 的覆盖区间为 $[l_1,r_1]$，质数 $b$ 的覆盖区间为 $[l_2,r_2]$，假设二者之间存在交集，则可以推出这两个区间一定需要划分在一个分组中，即这两个区间可以合并为 $[\min(l_1,l_2),\max(r_1,r_2)]$，参考「6313. 统计将重叠区间合并成组的方案数」我们找到左侧第一个不相交的集合并从该处划分开即可。
    假设存在数组 $[2,6,4,3]$，此时我们知道含有质因子 $2$ 必须要划分在一起的区间为 $[0,2]$，含有质因子 $3$ 必须要划分在一起的区间为 $[1,3]$，此时由于二者存在交集，因此 $[0,4]$ 这个区间中所有数必须要划分在同一个分组中，否则不能满足题目要求。
  3. 我们将质因子覆盖的区间从小到大进行排序，并对从左到右进行合并，找到第一个不想交的区间，即可从此处划分开来。
  4. 复杂度分析：
  • 时间复杂度：$O(n \log U )$，其中 $n$ 为数组的长度，$U$ 表示数组中的最大元素。
  • 空间复杂度：$O(\log U)$。

代码

class Solution {
public:
    int findValidSplit(vector<int>& nums) {
        int maxVal = *max_element(nums.begin(), nums.end());
        int n = nums.size();
        int m = sqrt(maxVal) + 3;
        vector<int> primer;
        vector<bool> visit(m + 1, false);
        for (int i = 2; i <= m; i++) {
            if (!visit[i]) {
                primer.emplace_back(i);
                for (int j = i; j <= m; j += i) {
                    visit[i] = true;
                }
            }
        }
        unordered_map<int, vector<int>> cnt;
        for (int i = 0; i < n; i++) {
            int x = nums[i];
            for (auto p : primer) {
                if (p > x) break;
                if (x % p) continue;
                cnt[p].emplace_back(i);
                while (x % p == 0) {
                    x /= p;
                }
            }
            if (x > 1) {
                cnt[x].emplace_back(i);
            }
        }
        if (cnt.size() <= 1) {
            return -1;
        }
        vector<pair<int, int>> arr;
        for (auto [_, v] : cnt) {
            arr.emplace_back(v[0], v.back());
        }
        sort(arr.begin(), arr.end());
        int i = 0;
        int last = arr[0].second;
        while (i < arr.size() && arr[i].first <= last) {
            last = max(last, arr[i].second);
            i++;
        }
        if (i < arr.size()) {
            return last;
        }
        return -1;        
    }
};

6310. 获得分数的方法数

考试中有 n 种类型的题目。给你一个整数 target 和一个下标从 0 开始的二维整数数组 types ，其中 types[i] = [counti, marksi] 表示第 i 种类型的题目有 counti 道，每道题目对应 marksi 分。

返回你在考试中恰好得到 target 分的方法数。由于答案可能很大，结果需要对 109 +7 取余。

注意，同类型题目无法区分。

  • 比如说，如果有 3 道同类型题目，那么解答第 1 和第 2 道题目与解答第 1 和第 3 道题目或者第 2 和第 3 道题目是相同的。

示例 1：

输入：target = 6, types = [[6,1],[3,2],[2,3]]
输出：7
解释：要获得 6 分，你可以选择以下七种方法之一：
- 解决 6 道第 0 种类型的题目：1 + 1 + 1 + 1 + 1 + 1 = 6
- 解决 4 道第 0 种类型的题目和 1 道第 1 种类型的题目：1 + 1 + 1 + 1 + 2 = 6
- 解决 2 道第 0 种类型的题目和 2 道第 1 种类型的题目：1 + 1 + 2 + 2 = 6
- 解决 3 道第 0 种类型的题目和 1 道第 2 种类型的题目：1 + 1 + 1 + 3 = 6
- 解决 1 道第 0 种类型的题目、1 道第 1 种类型的题目和 1 道第 2 种类型的题目：1 + 2 + 3 = 6
- 解决 3 道第 1 种类型的题目：2 + 2 + 2 = 6
- 解决 2 道第 2 种类型的题目：3 + 3 = 6

示例 2：

输入：target = 5, types = [[50,1],[50,2],[50,5]]
输出：4
解释：要获得 5 分，你可以选择以下四种方法之一：
- 解决 5 道第 0 种类型的题目：1 + 1 + 1 + 1 + 1 = 5
- 解决 3 道第 0 种类型的题目和 1 道第 1 种类型的题目：1 + 1 + 1 + 2 = 5
- 解决 1 道第 0 种类型的题目和 2 道第 1 种类型的题目：1 + 2 + 2 = 5
- 解决 1 道第 2 种类型的题目：5

示例 3：

输入：target = 18, types = [[6,1],[3,2],[2,3]]
输出：1
解释：只有回答所有题目才能获得 18 分。

提示：

  • 1 <= target <= 1000
  • n == types.length
  • 1 <= n <= 50
  • types[i].length == 2
  • 1 <= counti, marksi <= 50

地址

https://leetcode.cn/contest/weekly-contest-335/problems/number-of-ways-to-earn-points/

题意

动态规划

思路

  1. 经典的动态规划，设 $dp[i][x]$ 表示在前 $i$ 组中取出分数为 $x$ 的方法数，此时我们可以得到递推公式:
    $$
    dp[i + 1][x] = \sum_{k=0}^{t_{i+1}[1]}dp[i][x - k * t_{i + 1}[0]]
    $$
    即最后一个分组的取值范围为 $k \times marks_i$，其中 $k \in [0, count_i]$，应该是经典的动态规划题目了。

  2. 复杂度分析：

  • 时间复杂度：$O(m \times n \times U)$，其中 $m$ 表示给定的分数，$n$ 表示题目类型的数目，$U$ 表示给定的题目最大数目。
  • 空间复杂度：$O(m \times n)$。其中 $m$ 表示给定的分数，$n$ 表示题目类型的数目。

代码

class Solution {
public:
    
    int waysToReachTarget(int target, vector<vector<int>>& types) {
        int n = types.size();
        long long mod = 1e9 + 7;
        vector<vector<long long>> dp(target + 1, vector<long long>(n + 1));
        dp[0][0] = 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= target; j++) {
                for (int k = 0; k <= types[i][0]; k++) {
                    int x = k * types[i][1] + j;
                    if (x <= target) {
                        dp[x][i + 1] = (dp[x][i + 1] + dp[j][i]) % mod;
                    }
                }
            }
        }
        return  dp[target][n];
    }
};

欢迎关注和打赏，感谢支持！

Tags: 力扣周赛 题解
← leetcode weekly biweekly contest 99 Awesome Courses →

扫描二维码，分享此文章