leetcode biweekly contest 97

本周的周赛题目基本上都偏向于数学问题，难得见到比较好的题目

6337. 统计桌面上的不同数字

给你一个正整数 n ，开始时，它放在桌面上。在 109 天内，每天都要执行下述步骤：

• 对于出现在桌面上的每个数字 x ，找出符合 1 <= i <= n 且满足 x % i == 1 的所有数字 i 。
• 然后，将这些数字放在桌面上。

返回在 109 天之后，出现在桌面上的 不同 整数的数目。

注意：

• 一旦数字放在桌面上，则会一直保留直到结束。
• % 表示取余运算。例如，14 % 3 等于 2 。

示例 1：

输入：n = 5
输出：4
解释：最开始，5 在桌面上。 
第二天，2 和 4 也出现在桌面上，因为 5 % 2 == 1 且 5 % 4 == 1 。 
再过一天 3 也出现在桌面上，因为 4 % 3 == 1 。 
在十亿天结束时，桌面上的不同数字有 2 、3 、4 、5 。

示例 2：

输入：n = 3 
输出：2
解释： 
因为 3 % 2 == 1 ，2 也出现在桌面上。 
在十亿天结束时，桌面上的不同数字只有两个：2 和 3 。 

提示：

• 1 <= n <= 100

地址

https://leetcode.cn/contest/weekly-contest-330/problems/count-distinct-numbers-on-board/

题意

直接模拟

思路

1. 简单题目直接模拟即可;
2. 复杂度分析：

• 时间复杂度：$O(n \log m)$。
• 空间复杂度：$O(m)$。

代码

class Solution {
public:
    vector<int> separateDigits(vector<int>& nums) {
        vector<int> ans;
        for (auto v : nums) {
            string s = to_string(v);
            for (auto c : s) {
                ans.emplace_back(c - '0');
            }
        }
        return ans;
    }
};

2554. 从一个范围内选择最多整数 I

给你一个整数数组 banned 和两个整数 n 和 maxSum 。你需要按照以下规则选择一些整数：

• 被选择整数的范围是 [1, n] 。
• 每个整数 至多 选择 一次 。
• 被选择整数不能在数组 banned 中。
• 被选择整数的和不超过 maxSum 。

请你返回按照上述规则 最多 可以选择的整数数目。

示例 1：

输入：banned = [1,6,5], n = 5, maxSum = 6
输出：2
解释：你可以选择整数 2 和 4 。
2 和 4 在范围 [1, 5] 内，且它们都不在 banned 中，它们的和是 6 ，没有超过 maxSum 。

示例 2：

输入：banned = [1,2,3,4,5,6,7], n = 8, maxSum = 1
输出：0
解释：按照上述规则无法选择任何整数。

示例 3：

输入：banned = [11], n = 7, maxSum = 50
输出：7
解释：你可以选择整数 1, 2, 3, 4, 5, 6 和 7 。
它们都在范围 [1, 7] 中，且都没出现在 banned 中，它们的和是 28 ，没有超过 maxSum 。

提示：

• 1 <= banned.length <= 104
• 1 <= banned[i], n <= 104
• 1 <= maxSum <= 109

地址

https://leetcode.cn/contest/biweekly-contest-97/problems/maximum-number-of-integers-to-choose-from-a-range-i/

题意

直接模拟

思路

1. 由于题目给定的数据 $n$ 太小，导致题目变的太简单了，应该不限制 $n$ 的话，题目就会难一些。我们直接枚举 $[1,n]$ 之间的元素然后进行测试即可求的最大的数目，此时我们直接从最小往最大开始筛选即可。
2. 复杂度分析：

• 时间复杂度：$O(n)$，其中 $n$ 为给定的数。
• 空间复杂度：$O(n)$。

代码

class Solution {
public:
    int maxCount(vector<int>& banned, int n, int maxSum) {
        int maxn = *max_element(banned.begin(), banned.end());
        maxn = max(maxn, n);
        vector<int> flag(maxn + 1);
        for (auto v : banned) {
            flag[v] = 1;
        }
        long long total = 0;
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            if (flag[i]) continue;
            if (total + i <= maxSum) {
                total += i;
                ans++;
            } else {
                break;
            }
        }
        return ans;
    }
};

2555. 两个线段获得的最多奖品

在 X轴 上有一些奖品。给你一个整数数组 prizePositions ，它按照 非递减 顺序排列，其中 prizePositions[i] 是第 i 件奖品的位置。数轴上一个位置可能会有多件奖品。再给你一个整数 k 。

你可以选择两个端点为整数的线段。每个线段的长度都必须是 k 。你可以获得位置在任一线段上的所有奖品（包括线段的两个端点）。注意，两个线段可能会有相交。

• 比方说 k = 2 ，你可以选择线段 [1, 3] 和 [2, 4] ，你可以获得满足 1 <= prizePositions[i] <= 3 或者 2 <= prizePositions[i] <= 4 的所有奖品 i 。

请你返回在选择两个最优线段的前提下，可以获得的 最多 奖品数目。

示例 1：

输入：prizePositions = [1,1,2,2,3,3,5], k = 2
输出：7
解释：这个例子中，你可以选择线段 [1, 3] 和 [3, 5] ，获得 7 个奖品。

示例 2：

输入：prizePositions = [1,2,3,4], k = 0
输出：2
解释：这个例子中，一个选择是选择线段 [3, 3] 和 [4, 4] ，获得 2 个奖品。

提示：

• 1 <= prizePositions.length <= 105
• 1 <= prizePositions[i] <= 109
• 0 <= k <= 109
• prizePositions 有序非递减。

地址

https://leetcode.cn/contest/biweekly-contest-97/problems/maximize-win-from-two-segments/

题意

二分查找或者双指针

思路

1. 首先题目中所有的元素都已经按照从小到大进行排序，我们设 $dp[i]$ 表示所有小于等于 $prizePositions[i]$ 时可以选择的最大值，假设我们当前遍历到第 $i$ 个坐标，此时我们可以选择在区间 $[prizePositions[i] - k, prizePositions[i]]$ 之间的奖品，然后再选择区间 $[0,prizePositions[i] - k]$ 的最大值，此时我们利用二分查找即可，双指针的做法类似的选择原理即可。
2. 复杂度分析

• 时间复杂度：时间复杂度为 $O(n \log n)$，$n$ 表示数组的长度。
• 空间复杂度：时间复杂度为 $O(n)$。

代码

• 二分查找：

  class Solution { public: int maximizeWin(vector<int>& prizePositions, int k) { int n = prizePositions.size(); vector<int> dp(n + 1); int ans = 0; for (int i = 0; i < n; i++) { int x = lower_bound(prizePositions.begin(), prizePositions.end(), prizePositions[i] - k) - prizePositions.begin(); ans = max(ans, i - x + 1 + dp[x]); dp[i + 1] = max(dp[i], i - x + 1); } return ans; } };

• 双指针:

  class Solution { public: int maximizeWin(vector<int>& prizePositions, int k) { int n = prizePositions.size(); vector<int> dp(n + 1); int ans = 0; for (int i = 0, l = 0; i < n; i++) { while (l < n && prizePositions[i] - prizePositions[l] > k) { l++; } ans = max(ans, i - l + 1 + dp[l]); dp[i + 1] = max(dp[i], i - l + 1); } return ans; } };

2556. 二进制矩阵中翻转最多一次使路径不连通

给你一个下标从 0 开始的 m x n 二进制 矩阵 grid 。你可以从一个格子 (row, col) 移动到格子 (row + 1, col) 或者 (row, col + 1) ，前提是前往的格子值为 1 。如果从 (0, 0) 到 (m - 1, n - 1) 没有任何路径，我们称该矩阵是 不连通 的。

你可以翻转 最多一个 格子的值（也可以不翻转）。你 不能翻转 格子 (0, 0) 和 (m - 1, n - 1) 。

如果可以使矩阵不连通，请你返回 true ，否则返回 false 。

注意 ，翻转一个格子的值，可以使它的值从 0 变 1 ，或从 1 变 0 。

示例 1：

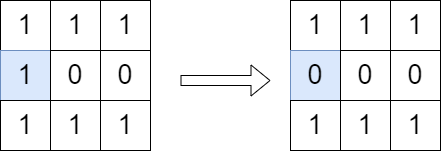
输入：grid = [[1,1,1],[1,0,0],[1,1,1]]
输出：true
解释：按照上图所示我们翻转蓝色格子里的值，翻转后从 (0, 0) 到 (2, 2) 没有路径。

示例 2：

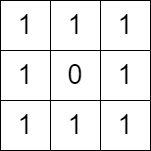
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：false
解释：无法翻转至多一个格子，使 (0, 0) 到 (2, 2) 没有路径。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• grid[0][0] == grid[m - 1][n - 1] == 1

地址

https://leetcode.cn/contest/biweekly-contest-96/problems/check-if-point-is-reachable/

题意

数学逻辑问题

思路

1. 题目很奇怪的问题，关键点在于每一步的走向下或者向右，题目完全变成了思维性的题目。比较有趣的题目，比如假设存在关键点 $x$，使得去掉该点后导致所有的路径都不通，则我们可以知道所有的路径一定都经过点 $x$，因此我们只需要找到一条可达的路径，则该路径一定经过点 $x$，然后我们将路径其中一条可达的路径全部设置为 $0$ 之后，然后再次检测起点到终点是否可达，如果可达则意味着一定存在其他路径，否则则认为修改后一个格子后就变为不可达。非常有意思的思考题目，如果理解透彻的话，则题目非常容易，否则变成了一个难题。
2. 复杂度分析：

• 时间复杂度：$O(mn)$。
• 空间复杂度：$O(1)$。

代码

class Solution {
public:
    bool isPossibleToCutPath(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        function<bool(int, int)> dfs = [&](int x, int y) {
            if (x == m - 1 && y == n - 1) {
                return true;
            }
            if (x >= m || y >= n) {
                return false;
            }
            grid[x][y] = 0;
            if (x + 1 < m && grid[x + 1][y] && dfs(x + 1, y)) {
                return true;
            }
            if (y + 1 < n && grid[x][y + 1] && dfs(x, y + 1)) {
                return true;
            }
            return false;
        };
        if(!dfs(0, 0)) {
            return true;
        }
        return !dfs(0, 0);
    }
};

欢迎关注和打赏，感谢支持！

• 关注我的博客: http://whistle-wind.com/
• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu
• 关注我的微信公众号: 公务程序猿