leetcode contest 329

周赛题目果真放水严重，难度下降很多。

6296. 交替数字和

给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号：

• 最高有效位 上的数字分配到 正 号。
• 剩余每位上数字的符号都与其相邻数字相反。

返回所有数字及其对应符号的和。

示例 1：

输入：n = 521
输出：4
解释：(+5) + (-2) + (+1) = 4

示例 2：

输入：n = 111
输出：1
解释：(+1) + (-1) + (+1) = 1

示例 3：

输入：n = 886996
输出：0
解释：(+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0

提示：

• 1 <= n <= 109

地址

https://leetcode.cn/contest/weekly-contest-329/problems/alternating-digit-sum/

题意

直接遍历

思路

1. 直接求出每一位数字的进行计算即可。
2. 复杂度分析：

• 时间复杂度：$O(n \log \max(nums))$。其中 $n$ 表示数组的长度。
• 空间复杂度：$O(1)$。

代码

class Solution {
public:
    int alternateDigitSum(int n) {
        string s = to_string(n);
        int res = 0, curr = 1;
        for (int i = 0; i < s.size(); i++) {
            res += curr * (s[i] - '0');
            curr *= -1;
        }
        return res;
    }
};

6297. 根据第 K 场考试的分数排序

班里有 m 位学生，共计划组织 n 场考试。给你一个下标从 0 开始、大小为 m x n 的整数矩阵 score ，其中每一行对应一位学生，而 score[i][j] 表示第 i 位学生在第 j 场考试取得的分数。矩阵 score 包含的整数 互不相同 。

另给你一个整数 k 。请你按第 k 场考试分数从高到低完成对这些学生（矩阵中的行）的排序。

返回排序后的矩阵。

示例 1：

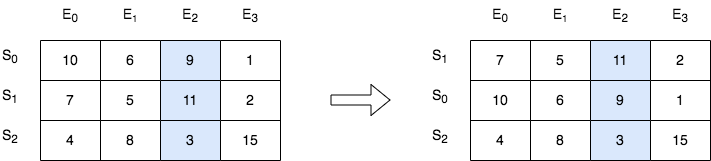
输入：score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
输出：[[7,5,11,2],[10,6,9,1],[4,8,3,15]]
解释：在上图中，S 表示学生，E 表示考试。
- 下标为 1 的学生在第 2 场考试取得的分数为 11 ，这是考试的最高分，所以 TA 需要排在第一。
- 下标为 0 的学生在第 2 场考试取得的分数为 9 ，这是考试的第二高分，所以 TA 需要排在第二。
- 下标为 2 的学生在第 2 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第三。

示例 2：

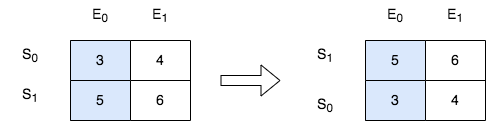
输入：score = [[3,4],[5,6]], k = 0
输出：[[5,6],[3,4]]
解释：在上图中，S 表示学生，E 表示考试。
- 下标为 1 的学生在第 0 场考试取得的分数为 5 ，这是考试的最高分，所以 TA 需要排在第一。
- 下标为 0 的学生在第 0 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第二。

提示：

• m == score.length
• n == score[i].length
• 1 <= m, n <= 250
• 1 <= score[i][j] <= 105
• score 由 不同 的整数组成
• 0 <= k < n

地址

https://leetcode.cn/contest/weekly-contest-329/problems/sort-the-students-by-their-kth-score/

题意

排序

思路

1. 我们直接将二维数组按照数组的第 $k$ 位元素从大到小进行排序即可。我们直接按照大小进行排序即可
2. 复杂度分析：

• 时间复杂度：$O(nm \log n)$，其中 $n$ 为矩阵的行数，$m$ 为矩阵的列数。
• 空间复杂度：$O(m \log n)$。

代码

class Solution {
public:
    vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {
        int m = score.size(), n = score[0].size();
        sort(score.begin(), score.end(), [&](vector<int> &a, vector<int> &b) {
            return a[k] > b[k];
        });
        return score;
    }
};

6299. 拆分数组的最小代价

给你一个整数数组 nums 和一个整数 k 。

将数组拆分成一些非空子数组。拆分的 代价 是每个子数组中的 重要性 之和。

令 trimmed(subarray) 作为子数组的一个特征，其中所有仅出现一次的数字将会被移除。

• 例如，trimmed([3,1,2,4,3,4]) = [3,4,3,4] 。

子数组的 重要性 定义为 k + trimmed(subarray).length 。

• 例如，如果一个子数组是 [1,2,3,3,3,4,4] ，trimmed([1,2,3,3,3,4,4]) = [3,3,3,4,4] 。这个子数组的重要性就是 k + 5 。

找出并返回拆分 nums 的所有可行方案中的最小代价。

子数组 是数组的一个连续 非空 元素序列。

示例 1：

输入：nums = [1,2,1,2,1,3,3], k = 2
输出：8
解释：将 nums 拆分成两个子数组：[1,2], [1,2,1,3,3]
[1,2] 的重要性是 2 + (0) = 2 。
[1,2,1,3,3] 的重要性是 2 + (2 + 2) = 6 。
拆分的代价是 2 + 6 = 8 ，可以证明这是所有可行的拆分方案中的最小代价。

示例 2：

输入：nums = [1,2,1,2,1], k = 2
输出：6
解释：将 nums 拆分成两个子数组：[1,2], [1,2,1] 。
[1,2] 的重要性是 2 + (0) = 2 。
[1,2,1] 的重要性是 2 + (2) = 4 。
拆分的代价是 2 + 4 = 6 ，可以证明这是所有可行的拆分方案中的最小代价。

示例 3：

输入：nums = [1,2,1,2,1], k = 5
输出：10
解释：将 nums 拆分成一个子数组：[1,2,1,2,1].
[1,2,1,2,1] 的重要性是 5 + (3 + 2) = 10 。
拆分的代价是 10 ，可以证明这是所有可行的拆分方案中的最小代价。

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] < nums.length
• 1 <= k <= 109

地址

https://leetcode.cn/problems/minimum-cost-to-split-an-array/

题意

动态规划

思路

1. 非常简单的动态规划，我们设 $dp[i]$ 表示前 $i$ 个元素完成拆分的最小代价，此时我们可以得到递推公式如下:
   $$
   dp[i] = \min(dp[i], dp[k] + cost[k + 1][i] + k) \quad k \in (0, i)
   $$
   即每次我们尝试最后拆分子数组的长度，即可得到前 $i$ 个元素的最小拆分代价，其中 $cost[i][j]$ 表示子数组 $nums[i,\cdots, j]$ 的重要性；
2. 我们求子数组的重要性可以用一个哈希表表示即可，非常简单的求子数组中存在重复元素的个数即可。
3. 复杂度分析

• 时间复杂度：时间复杂度为 $O(n^2)$，$n$ 表示数组的长度。
• 空间复杂度：时间复杂度为 $O(n)$。

代码

class Solution {
public:
    int minCost(vector<int>& nums, int k) {
        int n = nums.size();
        vector<long long> dp(n + 1, LONG_MAX);
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {
            int cost = k;
            vector<int> cnt(n + 1);
            for (int j = 1; j <= i; j++) {
                int x = nums[i - j];
                cnt[x]++;
                if (cnt[x] == 2) {
                    cost += 2;
                } else if (cnt[x] > 2) {
                    cost++;
                }
                dp[i] = min(dp[i], dp[i - j] + cost);
            }
        }
        return dp[n];
    }
};

6298. 执行逐位运算使字符串相等

给你两个下标从 0 开始的 二元 字符串 s 和 target ，两个字符串的长度均为 n 。你可以对 s 执行下述操作 任意 次：

• 选择两个 不同 的下标 i 和 j ，其中 0 <= i, j < n 。
• 同时，将 s[i] 替换为 (s[i] OR s[j]) ，s[j] 替换为 (s[i] XOR s[j]) 。

例如，如果 s = "0110" ，你可以选择 i = 0 和 j = 2，然后同时将 s[0] 替换为 (s[0] OR s[2] = 0 OR 1 = 1)，并将 s[2] 替换为 (s[0] XOR s[2] = 0 XOR 1 = 1)，最终得到 s = "1110" 。

如果可以使 s 等于 target ，返回 true ，否则，返回 false 。

示例 1：

输入：s = "1010", target = "0110"
输出：true
解释：可以执行下述操作：
- 选择 i = 2 和 j = 0 ，得到 s = "0010".
- 选择 i = 2 和 j = 1 ，得到 s = "0110".
可以使 s 等于 target ，返回 true 。

示例 2：

输入：s = "11", target = "00"
输出：false
解释：执行任意次操作都无法使 s 等于 target 。

提示：

• n == s.length == target.length
• 2 <= n <= 105
• s 和 target 仅由数字 0 和 1 组成

地址

https://leetcode.cn/contest/weekly-contest-329/problems/apply-bitwise-operations-to-make-strings-equal/

题意

数学问题

思路

1. 我们可以看到字符串 $s$ 中只要存在 $1$，即可按照以下规则:

• 将 $(0,1)$ 变为 $(1,1)$;
• 将 $(1,1)$ 变为 $(0,1)$;
  因此我们只需要检测字符串中是否存在 $1$ 即可，如果字符串中只有 $0$ 是无法进行替换的。当然实际比赛时用的分类讨论：
• 两个字符串如果相等，则直接返回；
• 如果字符串 $s$ 中存在不需要转换的 $1$ 则直接可以进行转换，我们可以把其他所有需要转换的 $0,1$ 进行转换；
• 如果字符串 $s$ 中同时存在需要转换的 $0$ 与 $1$，此时我们一定可以转换出一个正确的 $1$ 出来，然后利用这个不需要再次转换的 $1$ 将其余所有需要转换的字符完成转换即可；

2. 复杂度分析

• 时间复杂度：时间复杂度为 $O(n)$，$n$ 表示字符串的长度。
• 空间复杂度：时间复杂度为 $O(1)$。

代码

class Solution {
public:
    bool makeStringsEqual(string s, string target) {
        if (s == target) {
            return true;
        }
        int n = s.size();
        int one = 0, diff0 = 0, diff1 = 0;
        for (int i = 0; i < n; i++) {
            if (s[i] == target[i]) {
                if (s[i] == '1') one++;
            } else {
                if (s[i] == '0') {
                    diff0++;
                } else {
                    diff1++;
                }
            }
        }
        if ((diff0 > 0 && diff1 > 0) || one > 0) {
            return true;
        }
        return false;
    }
};

欢迎关注和打赏，感谢支持！

• 关注我的博客: http://whistle-wind.com/
• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu
• 关注我的微信公众号: 公务程序猿