leetcode contest 324

周赛的第四题太过于简单了，只能说是送分题了。第三题出的挺好，是个思维题目，现在这种类型的题目希望多出来一些。

6265. 统计相似字符串对的数目

给你一个下标从 0 开始的字符串数组 words 。

如果两个字符串由相同的字符组成，则认为这两个字符串相似。

例如，"abca" 和 "cba" 相似，因为它们都由字符 'a'、'b'、'c' 组成。
然而，"abacba" 和 "bcfd" 不相似，因为它们不是相同字符组成的。

请你找出满足字符串 words[i] 和 words[j] 相似的下标对 (i, j) ，并返回下标对的数目，其中 0 <= i < j <= word.length - 1 。

示例 1：

输入：words = ["aba","aabb","abcd","bac","aabc"]
输出：2
解释：共有 2 对满足条件：
- i = 0 且 j = 1 ：words[0] 和 words[1] 只由字符 'a' 和 'b' 组成。 
- i = 3 且 j = 4 ：words[3] 和 words[4] 只由字符 'a'、'b' 和 'c' 。

示例 2：

输入：words = ["aabb","ab","ba"]
输出：3
解释：共有 3 对满足条件：
- i = 0 且 j = 1 ：words[0] 和 words[1] 只由字符 'a' 和 'b' 组成。 
- i = 0 且 j = 2 ：words[0] 和 words[2] 只由字符 'a' 和 'b' 组成。 
- i = 1 且 j = 2 ：words[1] 和 words[2] 只由字符 'a' 和 'b' 组成。

示例 3：

输入：words = ["nba","cba","dba"]
输出：0
解释：不存在满足条件的下标对，返回 0 。

提示：

1 <= words.length <= 100
1 <= words[i].length <= 100
words[i] 仅由小写英文字母组成

地址

https://leetcode.cn/contest/weekly-contest-324/problems/count-pairs-of-similar-strings/

题意

直接遍历

思路

统计每个字符串中出现字符的统计情况，然后依次找到出现字符串相同的字符串组合数目即可。
复杂度分析：

时间复杂度：$O(nm + n^2 \times |\Sigma|)$。其中 $n$ 表示数组的长度，$|\Sigma|$ 表示字符集，在这里 $|\Sigma| = 26$。
空间复杂度：$O(|\Sigma|)$。

代码

class Solution {
public:
    int similarPairs(vector<string>& words) {
        int n = words.size();
        vector<vector<bool>> cnt(n, vector<bool>(26));
        for (int i = 0; i < n; i++) {
            for (auto c : words[i]) {
                cnt[i][c - 'a'] = true;
            }
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (cnt[i] == cnt[j]) {
                    ans++;
                }
            }
        }
        return ans;
    }
};

6266. 使用质因数之和替换后可以取到的最小值

给你一个正整数 n 。

请你将 n 的值替换为 n 的 质因数 之和，重复这一过程。

注意，如果 n 能够被某个质因数多次整除，则在求和时，应当包含这个质因数同样次数。

返回 n 可以取到的最小值。

示例 1：

输入：n = 15
输出：5
解释：最开始，n = 15 。
15 = 3 * 5 ，所以 n 替换为 3 + 5 = 8 。
8 = 2 * 2 * 2 ，所以 n 替换为 2 + 2 + 2 = 6 。
6 = 2 * 3 ，所以 n 替换为 2 + 3 = 5 。
5 是 n 可以取到的最小值。

示例 2：

输入：n = 3
输出：3
解释：最开始，n = 3 。
3 是 n 可以取到的最小值。

提示：

2 <= n <= 105

地址

https://leetcode.cn/contest/weekly-contest-324/problems/smallest-value-after-replacing-with-sum-of-prime-factors/

题意

数学

思路

本质就是模拟即可，首先我们可以利用素数筛选法，找到 $n$ 以内的所有素数，然后依次进行模拟除法直到除法后的结果与原值相等为止结束。
复杂度分析：

时间复杂度：$O(n)$，其中 $n$ 为给定的数。最优的情况的下变换一次 $n$ 变为 $\dfrac{n}{2} + 2$，所以最多需要给定的元素变换即可
空间复杂度：$O(n)$，需要

代码

class Solution {
public:
    
    int smallestValue(int n) {
        vector<int> primer;
        vector<bool> visit(n + 1, false);
        for (int i = 2; i <= n; i++) {
            if (!visit[i]) {
                primer.emplace_back(i);
                for (int j = i; j <= n; j += i) {
                    visit[j] = true;
                }
            }
        }
        
        while (true) {
            int next = 0;
            int curr = n;
            for (auto v : primer) {
                if (v > n) break;
                while ((n % v) == 0) {
                    next += v;
                    n /= v;
                }
            }
            if (curr == next) {
                return next;
            } else {
                n = next;
            }
        } 
        return n;
    }
};

6267. 添加边使所有节点度数都为偶数

显示英文描述

给你一个有 n 个节点的无向图，节点编号为 1 到 n 。再给你整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条边。图不一定连通。

你可以给图中添加至多两条额外的边（也可以一条边都不添加），使得图中没有重边也没有自环。

如果添加额外的边后，可以使得图中所有点的度数都是偶数，返回 true ，否则返回 false 。

点的度数是连接一个点的边的数目。

示例 1：

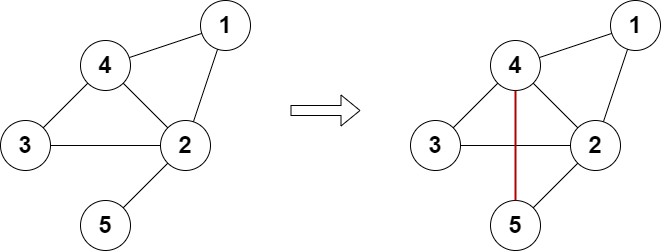
输入：n = 5, edges = [[1,2],[2,3],[3,4],[4,2],[1,4],[2,5]]
输出：true
解释：上图展示了添加一条边的合法方案。
最终图中每个节点都连接偶数条边。

示例 2：

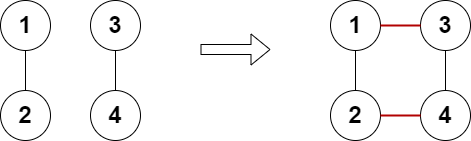
输入：n = 4, edges = [[1,2],[3,4]]
输出：true
解释：上图展示了添加两条边的合法方案。

示例 3：

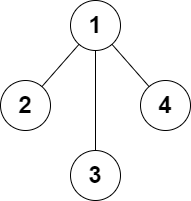
输入：n = 4, edges = [[1,2],[1,3],[1,4]]
输出：false
解释：无法添加至多 2 条边得到一个符合要求的图。

提示：

3 <= n <= 105
2 <= edges.length <= 105
edges[i].length == 2
1 <= ai, bi <= n
ai != bi
图中不会有重边

地址

https://leetcode.cn/contest/weekly-contest-324/problems/add-edges-to-make-degrees-of-all-nodes-even/

题意

思维题目

思路

这个题目实际比较有意思，本质是个思维的问题，可能不需要特别复杂的技巧。分析如下：

如果使得所有顶点的度都为偶数，首先我们需要找到所有度为奇数的顶点，此时我们直接统计所有顶点的度数即可；
我们仔细分析可以知道顶点度数为奇数的顶点最多只能有 $4$ 个，因此我们分情况来进行讨论:
度数位奇数的顶点数目为 $0$ 个：此时所有的顶点的度数均为偶数，则直接返回 $false$；
度数位奇数的顶点数目为 $1$ 个：此时由于顶点不能含有自环，因此此时我们无法往这个顶点上加边数使得该顶点的度数为偶数，由于 $1$ 条边连着两个不同的顶点，因此我们无法完成；
度数位奇数的顶点数目为 $2$ 个：此时就非常有意思了，可以有多种情况分析：
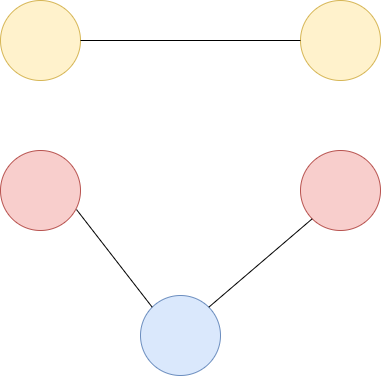
- 假设这两个顶点之间没有边，我们直接将这两个顶点连起来，使得每个顶点都增加 $1$ 条边，从而使得两个顶点的度数均变为偶数；
- 假设这两个顶点之间有边，但这两个顶点与某个顶点 $p$ 都不存在边，此时就将 $p$ 分别与这两个顶点相连，使得每个顶点都增加 $1$ 条边，从而使得两个顶点的度数均变为偶数；
- 上述两种情况都不满足，则不存在可以使得两个顶点的度数均为偶数的解决办法；
度数位奇数的顶点数目为 $3$ 个：此时最多只能加两条边，无论如何增加均无法满足；
度数位奇数的顶点数目为 $4$ 个：此时只需要找到 $4$ 个顶点是否存在不想交的两对顶点，且顶点对之间不存在边即可。

复杂度分析

时间复杂度：时间复杂度为 $O(V + E)$，$V$ 表示顶点的数学，$E$ 表示边的数目。
空间复杂度：时间复杂度为 $O(V + E)$。

代码

class Solution {
public:
    bool isPossible(int n, vector<vector<int>>& edges) {
        vector<unordered_set<int>> graph(n + 1);
        for (auto v : edges) {
            graph[v[0]].emplace(v[1]);
            graph[v[1]].emplace(v[0]);
        }
        vector<int> vertex;
        for (int i = 1; i <= n; i++) {
            if (graph[i].size() % 2) {
                vertex.emplace_back(i);
            }
        }
        if (vertex.size() == 0) {
            return true;
        } else if (vertex.size() == 2) {
            int a = vertex[0], b = vertex[1];
            if (!graph[a].count(b)) {
                return true;
            } else {
                for (int i = 1; i <= n; i++) {
                    if (a != i && b != i && !graph[i].count(a) && !graph[i].count(b)) {
                        return true;
                    }
                }
                return false;
            }
        } else if (vertex.size() == 1 || vertex.size() == 3) {
            return false;
        } else if (vertex.size() == 4) {
            int a = vertex[0], b = vertex[1], c = vertex[2], d = vertex[3];
            return !graph[a].count(b) && !graph[c].count(d) ||
                   !graph[a].count(c) && !graph[b].count(d) ||
                   !graph[a].count(d) && !graph[b].count(c);
        }
        return false;
    }
};

6268. 查询树中环的长度

给你一个整数 n ，表示你有一棵含有 2n - 1 个节点的 完全二叉树 。根节点的编号是 1 ，树中编号在[1, 2n - 1 - 1] 之间，编号为 val 的节点都有两个子节点，满足：

左子节点的编号为 2 * val
右子节点的编号为 2 * val + 1

给你一个长度为 m 的查询数组 queries ，它是一个二维整数数组，其中 queries[i] = [ai, bi] 。对于每个查询，求出以下问题的解：

在节点编号为 ai 和 bi 之间添加一条边。
求出图中环的长度。
删除节点编号为 ai 和 bi 之间新添加的边。

注意：

环是开始和结束于同一节点的一条路径，路径中每条边都只会被访问一次。
环的长度是环中边的数目。
在树中添加额外的边后，两个点之间可能会有多条边。

请你返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 个查询的结果。

示例 1：

输入：n = 3, queries = [[5,3],[4,7],[2,3]]
输出：[4,5,3]
解释：上图是一棵有 23 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 3 和节点 5 之间添加边后，环为 [5,2,1,3] ，所以第一个查询的结果是 4 。删掉添加的边后处理下一个查询。
- 在节点 4 和节点 7 之间添加边后，环为 [4,2,1,3,7] ，所以第二个查询的结果是 5 。删掉添加的边后处理下一个查询。
- 在节点 2 和节点 3 之间添加边后，环为 [2,1,3] ，所以第三个查询的结果是 3 。删掉添加的边。

示例 2：

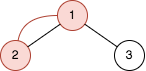
输入：n = 2, queries = [[1,2]]
输出：[2]
解释：上图是一棵有 22 - 1 个节点的树。红色节点表示添加额外边后形成环的节点。
- 在节点 1 和节点 2 之间添加边后，环为 [2,1] ，所以第一个查询的结果是 2 。删掉添加的边。

提示：

2 <= n <= 30
m == queries.length
1 <= m <= 105
queries[i].length == 2
1 <= ai, bi <= 2n - 1
ai != bi

地址

https://leetcode.cn/contest/weekly-contest-324/problems/cycle-length-queries-in-a-tree/

题意

LCA问题

思路

本题实际真心算不上 $hard$ 问题，确实太过于简单了，本质为求二叉树中两个节点的最近公共祖先的问题，设给定点 $(a,b)$, 假设两点的最近公共祖先为点 $p$，则构成的环的大小为 $a$ 到 $p$ 的距离加上 $b$ 到 $p$ 距离再加上 $1$，求 $lca$ 的方法和技巧很多，在此不再描述，最简单的莫过于求二者到根节点的公共路径。
复杂度分析：

时间复杂度：$O(nm)$，其中 $m$ 表示查询的次数。
空间复杂度：$O(n)$，其中 $n$ 表示给定的数。

代码

class Solution {
public:
    int dist(int x, int y) {
        vector<int> path1, path2;
        path1.emplace_back(x);
        while (x > 1) {
            x /= 2;
            path1.emplace_back(x);
        }
        
        path2.emplace_back(y);
        while (y > 1) {
            y /= 2;
            path2.emplace_back(y);
        }
        reverse(path1.begin(), path1.end());
        reverse(path2.begin(), path2.end());
        int res = path1.size() + path2.size() - 2;
        for (int i = 1; i < path1.size() && i < path2.size(); i++) {
            if (path1[i] == path2[i]) {
                res -= 2;
            } else {
                break;
            }
        }
        return res;
    }
    
    vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {
        int m = queries.size();
        vector<int> res;
        for (auto v : queries) {
            int x = v[0],  y = v[1];
            res.emplace_back(dist(x, y) + 1);
        }
        return res;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 力扣周赛题解

← leetcode biweekly contest 93 【MIT6.S081】lab11 network →

扫描二维码，分享此文章