leetcode contest 323

周赛的题目又是大放水了，感觉双周赛的题目比较难，周赛的题目放水的概率非常高。

6257. 删除每行中的最大值

给你一个 m x n 大小的矩阵 grid ，由若干正整数组成。

执行下述操作，直到 grid 变为空矩阵：

• 从每一行删除值最大的元素。如果存在多个这样的值，删除其中任何一个。
• 将删除元素中的最大值与答案相加。

注意 每执行一次操作，矩阵中列的数据就会减 1 。

返回执行上述操作后的答案。

示例 1：

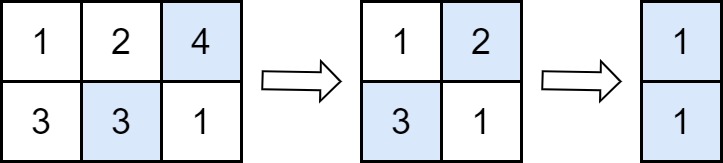
输入：grid = [[1,2,4],[3,3,1]]
输出：8
解释：上图展示在每一步中需要移除的值。
- 在第一步操作中，从第一行删除 4 ，从第二行删除 3（注意，有两个单元格中的值为 3 ，我们可以删除任一）。在答案上加 4 。
- 在第二步操作中，从第一行删除 2 ，从第二行删除 3 。在答案上加 3 。
- 在第三步操作中，从第一行删除 1 ，从第二行删除 1 。在答案上加 1 。
最终，答案 = 4 + 3 + 1 = 8 。

示例 2：

输入：grid = [[10]]
输出：10
解释：上图展示在每一步中需要移除的值。
- 在第一步操作中，从第一行删除 10 。在答案上加 10 。
最终，答案 = 10 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 1 <= grid[i][j] <= 100

地址

https://leetcode.cn/contest/weekly-contest-323/problems/delete-greatest-value-in-each-row/

题意

直接遍历

思路

1. 将矩阵的每一行按照从小到大排序，每次我们取出每一列的最大值即可。
2. 复杂度分析：

• 时间复杂度：$O(mn\log n)$。
• 空间复杂度：$O(\log)$。

代码

class Solution {
public:
    int deleteGreatestValue(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        for (int i = 0; i < m; i++) {
            sort(grid[i].begin(), grid[i].end());
        }
        int res = 0;
        for (int i = 0; i < n; i++) {
            int maxVal = 0;
            for (int j = 0; j < m; j++) {
                maxVal = max(maxVal, grid[j][i]);
            }
            res += maxVal;
        }
        return res;
    }
};

6258. 数组中最长的方波

给你一个整数数组 nums 。如果 nums 的子序列满足下述条件，则认为该子序列是一个 方波 ：

• 子序列的长度至少为 2 ，并且
• 将子序列从小到大排序 之后 ，除第一个元素外，每个元素都是前一个元素的 平方 。

返回 nums 中 最长方波 的长度，如果不存在 方波 则返回 -1 。

子序列 也是一个数组，可以由另一个数组删除一些或不删除元素且不改变剩余元素的顺序得到。

示例 1 ：

输入：nums = [4,3,6,16,8,2]
输出：3
解释：选出子序列 [4,16,2] 。排序后，得到 [2,4,16] 。
- 4 = 2 * 2.
- 16 = 4 * 4.
因此，[4,16,2] 是一个方波.
可以证明长度为 4 的子序列都不是方波。

示例 2 ：

输入：nums = [2,3,5,6,7]
输出：-1
解释：nums 不存在方波，所以返回 -1 。

提示：

• 2 <= nums.length <= 105
• 2 <= nums[i] <= 105

地址

https://leetcode.cn/contest/weekly-contest-323/problems/longest-square-streak-in-an-array/

题意

动态规划

思路

1. 由于题目中方波数组的顺序必须满足从小到大排列，我们设 $dp[x]$ 表示以 $x$ 为结尾的方波数组的最长长度，则 $dp[x] = dp[\sqrt{x}] + 1$。我们找到最长的方波数组长度即可。
2. 复杂度分析：

• 时间复杂度：$O(n \log n)$，其中 $n$ 为数组的元素个数。
• 空间复杂度：$O(\log n)$，其中 $n$ 为数组的元素的个数。

代码

class Solution {
public:
    int longestSquareStreak(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        unordered_map<int, int> dp;
        int res = -1;
        for (int i = 0; i < n; i++) {
            dp[nums[i]] = 1;
            int x = sqrt(nums[i]);
            if (x * x == nums[i]) {
                dp[nums[i]] = dp[x] + 1;
            } 
            if (dp[nums[i]] > 1) {
                res = max(res, dp[nums[i]]);
            }
        }
        return res;
    }
};

6259. 设计内存分配器

给你一个整数 n ，表示下标从 0 开始的内存数组的大小。所有内存单元开始都是空闲的。

请你设计一个具备以下功能的内存分配器：

1. 分配 一块大小为 size 的连续空闲内存单元并赋 id mID 。
2. 释放 给定 id mID 对应的所有内存单元。

注意：

• 多个块可以被分配到同一个 mID 。
• 你必须释放 mID 对应的所有内存单元，即便这些内存单元被分配在不同的块中。

实现 Allocator 类：

• Allocator(int n) 使用一个大小为 n 的内存数组初始化 Allocator 对象。
• int allocate(int size, int mID) 找出大小为 size 个连续空闲内存单元且位于 最左侧 的块，分配并赋 id mID 。返回块的第一个下标。如果不存在这样的块，返回 -1 。
• int free(int mID) 释放 id mID 对应的所有内存单元。返回释放的内存单元数目。

示例：

输入
["Allocator", "allocate", "allocate", "allocate", "free", "allocate", "allocate", "allocate", "free", "allocate", "free"]
[[10], [1, 1], [1, 2], [1, 3], [2], [3, 4], [1, 1], [1, 1], [1], [10, 2], [7]]
输出
[null, 0, 1, 2, 1, 3, 1, 6, 3, -1, 0]

解释
Allocator loc = new Allocator(10); // 初始化一个大小为 10 的内存数组，所有内存单元都是空闲的。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 0 。内存数组变为 [1, , , , , , , , , ]。返回 0 。
loc.allocate(1, 2); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,2, , , , , , , , ]。返回 1 。
loc.allocate(1, 3); // 最左侧的块的第一个下标是 2 。内存数组变为 [1,2,3, , , , , , , ]。返回 2 。
loc.free(2); // 释放 mID 为 2 的所有内存单元。内存数组变为 [1, ,3, , , , , , , ] 。返回 1 ，因为只有 1 个 mID 为 2 的内存单元。
loc.allocate(3, 4); // 最左侧的块的第一个下标是 3 。内存数组变为 [1, ,3,4,4,4, , , , ]。返回 3 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 1 。内存数组变为 [1,1,3,4,4,4, , , , ]。返回 1 。
loc.allocate(1, 1); // 最左侧的块的第一个下标是 6 。内存数组变为 [1,1,3,4,4,4,1, , , ]。返回 6 。
loc.free(1); // 释放 mID 为 1 的所有内存单元。内存数组变为 [ , ,3,4,4,4, , , , ] 。返回 3 ，因为有 3 个 mID 为 1 的内存单元。
loc.allocate(10, 2); // 无法找出长度为 10 个连续空闲内存单元的空闲块，所有返回 -1 。
loc.free(7); // 释放 mID 为 7 的所有内存单元。内存数组保持原状，因为不存在 mID 为 7 的内存单元。返回 0 。

提示：

• 1 <= n, size, mID <= 1000
• 最多调用 allocate 和 free 方法 1000 次

地址

https://leetcode.cn/contest/weekly-contest-323/problems/design-memory-allocator/

题意

直接模拟

思路

1. 由于给定的数据量太小，直接暴力模拟即可，没有什么太大的难度，这个题目出的比较失败，至少应该将数量级到达 $10^4$ 以上。
2. 复杂度分析

• 时间复杂度：时间复杂度为 $O(nm)$，$n$ 表示给定的数组的长度， $m$ 表示调用的函数的次数。
• 空间复杂度：空间复杂度为 $O(n)$，$n$ 表示给定的数组的长度。

代码

class Allocator {
public:
    Allocator(int n) {
        mem = vector<int>(n);
    }
    
    int allocate(int size, int mID) {
        int i = 0;
        while (i < mem.size()) {
            if (mem[i] == 0) {
                int start = i;
                while (i < mem.size() && mem[i] == 0) {
                    i++;
                }
                if (i - start >= size) {
                    for (int i = start; i < start + size; i++) {
                        mem[i] = mID;
                    }
                    return start;
                }
            } else {
                i++;
            }
        }
        return -1;
    }
    
    int free(int mID) {
        int res = 0;
        for (int i = 0; i < mem.size(); i++) {
            if (mem[i] == mID) {
                mem[i] = 0;
                res++;
            }
        }
        return res;
    }
private:
    vector<int> mem;
};

6260. 矩阵查询可获得的最大分数

给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。

找出一个大小为 k 的数组 answer ，且满足对于每个整数 queres[i] ，你从矩阵 左上角 单元格开始，重复以下过程：

• 如果 queries[i] 严格 大于你当前所处位置单元格，如果该单元格是第一次访问，则获得 1 分，并且你可以移动到所有 4 个方向（上、下、左、右）上任一 相邻 单元格。
• 否则，你不能获得任何分，并且结束这一过程。

在过程结束后，answer[i] 是你可以获得的最大分数。注意，对于每个查询，你可以访问同一个单元格 多次 。

返回结果数组 answer 。

示例 1：

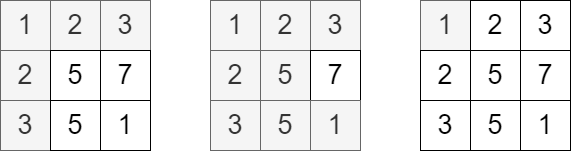
输入：grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出：[5,8,1]
解释：上图展示了每个查询中访问并获得分数的单元格。

示例 2：

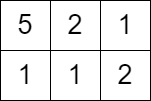
输入：grid = [[5,2,1],[1,1,2]], queries = [3]
输出：[0]
解释：无法获得分数，因为左上角单元格的值大于等于 3 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• k == queries.length
• 1 <= k <= 104
• 1 <= grid[i][j], queries[i] <= 106

地址

https://leetcode.cn/contest/weekly-contest-323/problems/maximum-number-of-points-from-grid-queries/

题意

离线查询 + 优先队列

思路

1. 题目出的不是很好，感觉太过于模板的题目，即且翻译的有问题，简单的来说即给定的 $x$，从 $(0,0)$ 出发可以遍历的所有小于 $x$ 的元素的数目。
2. 本题的解法有多种，首先我们只需将所有的查询从小到大进行排序，从而我们可以将矩阵从小到大进行遍历。

• 优先队列: 我们从 $(0,0)$ 压入到优先队列，每次查询 $x$ 时，我们将队列中所有严格小于 $x$ 的元素 $(x,y)$ 弹出并计数，并同时将 $(x,y)$ 四个方向上相邻的元素压入到队列中，这样保证队列中待访问且所有符合要求的元素全部从队列中弹出。我们计数所有当前已弹出的元素为 $tot$，满足小于 $x$ 的元素的个数即为 $tot$。
• 并查集: 将矩阵所有的元素按照从小到大进行排序，每次查询 $x$ 时将所有小于 $x$ 的矩阵中的元素与其相邻的边进行聚合，最后我们查询 $(0,0)$ 所在的连通单元的单元的数目即可。

3. 复杂度分析：

• 时间复杂度：$O(q \log q + q \times (\log mn))$，其中 $q$ 表示查询的次数，$m,n$ 表示矩阵的行与列。
• 空间复杂度：$O(mn)$，其中 $m,n$ 表示矩阵的行与列。

代码

• 优先队列

  class Solution { public: vector<int> maxPoints(vector<vector<int>>& grid, vector<int>& queries) { int m = grid.size(); int n = grid[0].size(); int k = queries.size(); vector<int> res(k); vector<pair<int,int>> arr; for (int i = 0; i < k; i++) { arr.emplace_back(queries[i], i); } sort(arr.begin(), arr.end()); vector<vector<bool>> visit(m, vector<bool>(n, false)); priority_queue<tuple<int,int,int>, vector<tuple<int,int,int>>, greater<tuple<int,int,int>>> pq; pq.emplace(grid[0][0], 0, 0); int tot = 0; visit[0][0] = true; int dir[4][2] = {{0, -1}, {0, 1}, {1, 0}, {-1, 0}}; for (int i = 0; i < k; i++) { while(!pq.empty() && get<0>(pq.top()) < arr[i].first) { auto [val, x, y] = pq.top(); pq.pop(); tot++; for (int j = 0; j < 4; j++) { int nx = x + dir[j][0]; int ny = y + dir[j][1]; if (nx >= 0 && nx < m && ny >= 0 && ny < n) { if (visit[nx][ny]) continue; pq.emplace(grid[nx][ny], nx, ny); visit[nx][ny] = true; } } } res[arr[i].second] = tot; } return res; } };

• 并查集

  class Solution { const int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; public: vector<int> maxPoints(vector<vector<int>> &grid, vector<int> &queries) { int m = grid.size(), n = grid[0].size(), mn = m * n; // 并查集模板 int fa[mn], size[mn]; iota(fa, fa + mn, 0); fill(size, size + mn, 1); function<int(int)> find = [&](int x) -> int { return fa[x] == x ? x : fa[x] = find(fa[x]); }; auto merge = [&](int from, int to) { from = find(from); to = find(to); if (from != to) { fa[from] = to; size[to] += size[from]; } }; // 矩阵元素从小到大排序，方便离线 array<int, 3> a[mn]; for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) a[i * n + j] = {grid[i][j], i, j}; sort(a, a + mn); // 查询的下标按照查询值从小到大排序，方便离线 int k = queries.size(), id[k]; iota(id, id + k, 0); sort(id, id + k, [&](int i, int j) { return queries[i] < queries[j]; }); vector<int> ans(k); int j = 0; for (int i : id) { int q = queries[i]; for (; j < mn && a[j][0] < q; ++j) { int x = a[j][1], y = a[j][2]; // 枚举周围四个格子，值小于 q 才可以合并 for (auto &d : dirs) { int x2 = x + d[0], y2 = y + d[1]; if (0 <= x2 && x2 < m && 0 <= y2 && y2 < n && grid[x2][y2] < q) merge(x * n + y, x2 * n + y2); // 把坐标压缩成一维的编号 } } if (grid[0][0] < q) ans[i] = size[find(0)]; // 左上角的连通块的大小 } return ans; } };

  欢迎关注和打赏，感谢支持！
• 关注我的博客: http://whistle-wind.com/
• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu
• 关注我的微信公众号: 公务程序猿