leetcode contest 322

前三题都是常规题目，最后一题并没有用到太多复杂的算法，两个 BFS 即可搞定。

6253. 回环句

句子是由单个空格分隔的一组单词，且不含前导或尾随空格。

例如，"Hello World"、"HELLO"、"hello world hello world" 都是符合要求的句子。

单词仅由大写和小写英文字母组成。且大写和小写字母会视作不同字符。

如果句子满足下述全部条件，则认为它是一个 回环句 ：

单词的最后一个字符和下一个单词的第一个字符相等。
最后一个单词的最后一个字符和第一个单词的第一个字符相等。

例如，"leetcode exercises sound delightful"、"eetcode"、"leetcode eats soul" 都是回环句。然而，"Leetcode is cool"、"happy Leetcode"、"Leetcode" 和 "I like Leetcode" 都不是回环句。

给你一个字符串 sentence ，请你判断它是不是一个回环句。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：sentence = "leetcode exercises sound delightful"
输出：true
解释：句子中的单词是 ["leetcode", "exercises", "sound", "delightful"] 。
- leetcode 的最后一个字符和 exercises 的第一个字符相等。
- exercises 的最后一个字符和 sound 的第一个字符相等。
- sound 的最后一个字符和 delightful 的第一个字符相等。
- delightful 的最后一个字符和 leetcode 的第一个字符相等。
这个句子是回环句。

示例 2：

输入：sentence = "eetcode"
输出：true
解释：句子中的单词是 ["eetcode"] 。
- eetcode 的最后一个字符和 eetcode 的第一个字符相等。
这个句子是回环句。

示例 3：

输入：sentence = "Leetcode is cool"
输出：false
解释：句子中的单词是 ["Leetcode", "is", "cool"] 。
- Leetcode 的最后一个字符和 is 的第一个字符 不 相等。 
这个句子 不 是回环句。

提示：

1 <= sentence.length <= 500
sentence 仅由大小写英文字母和空格组成
sentence 中的单词由单个空格进行分隔
不含任何前导或尾随空格

地址

https://leetcode.cn/contest/weekly-contest-322/problems/circular-sentence/

题意

直接遍历

思路

直接将字符串切分为单词，然后依次检测相邻的单词是否符合回环的条件即可。
复杂度分析：

时间复杂度：$O(1)$。
空间复杂度：$O(n)$。可以优化到 $O(1)$。

代码

class Solution {
public:
    bool isCircularSentence(string sentence) {
        vector<string> arr;
        int i = 0;
        while(i < sentence.size()) {
            if (sentence[i] != ' ') {
                string s;
                while(i < sentence.size() && sentence[i] != ' ') {
                    s.push_back(sentence[i]);
                    i++;
                }
                arr.emplace_back(s);
            } else {
                i++;
            }
        }
        int m = arr.size();
        for (int i = 0; i < arr.size(); i++) {
            if (arr[i].back() != arr[(i + 1) % m][0]) {
                return false;
            }
        }
        return true;
    }
};

6254. 划分技能点相等的团队

给你一个正整数数组 skill ，数组长度为偶数 n ，其中 skill[i] 表示第 i 个玩家的技能点。将所有玩家分成 n / 2 个 2 人团队，使每一个团队的技能点之和相等。

团队的 化学反应 等于团队中玩家的技能点乘积。

返回所有团队的 化学反应 之和，如果无法使每个团队的技能点之和相等，则返回 -1 。

示例 1：

输入：skill = [3,2,5,1,3,4]
输出：22
解释：
将玩家分成 3 个团队 (1, 5), (2, 4), (3, 3) ，每个团队的技能点之和都是 6 。
所有团队的化学反应之和是 1 * 5 + 2 * 4 + 3 * 3 = 5 + 8 + 9 = 22 。

示例 2：

输入：skill = [3,4]
输出：12
解释：
两个玩家形成一个团队，技能点之和是 7 。
团队的化学反应是 3 * 4 = 12 。

示例 3：

输入：skill = [1,1,2,3]
输出：-1
解释：
无法将玩家分成每个团队技能点都相等的若干个 2 人团队。

提示：

2 <= skill.length <= 105
skill.length 是偶数
1 <= skill[i] <= 1000

地址

https://leetcode.cn/contest/weekly-contest-322/problems/divide-players-into-teams-of-equal-skill/

题意

数学问题

思路

题目要求数组中的元素可以分为 $\dfrac{n}{2}$ 个团队，且每个对中两个名成员的机能之和相等，则可以推出如下:

数组中的所有元素和 $sum$ 一定能被 $\dfrac{n}{2}$，且每两个成员中的和为 $x = \dfrac{2 \times sum}{n}$;
我们直接将数组按照从小到大进行排序，可以知道 $skill[i] + skill[n-i-1] = x$，我们依次判断即可。

复杂度分析：

时间复杂度：$O(n \log n)$，其中 $n$ 为数组的元素。
空间复杂度：$O(\og n)$，其中 $n$ 为数组的元素。

代码

class Solution {
public:
    long long dividePlayers(vector<int>& skill) {
        long long tot = accumulate(skill.begin(), skill.end(), 0LL);
        int n = skill.size();
        int m = n / 2;
        if (tot % m != 0) {
            return -1;
        }
        int val = tot / m;
        long long res = 0;
        sort(skill.begin(), skill.end());
        for (int i = 0; i < m; i++) {
            if (skill[i] + skill[n - i - 1] != val) {
                 return -1;
            }
            res += skill[i] * skill[n - i - 1];
        }
        return res;
    }
};

6255. 两个城市间路径的最小分数

给你一个正整数 n ，表示总共有 n 个城市，城市从 1 到 n 编号。给你一个二维数组 roads ，其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条双向道路，道路距离为 distancei 。城市构成的图不一定是连通的。

两个城市之间一条路径的分数定义为这条路径中道路的最小距离。

城市 1 和城市 n 之间的所有路径的最小分数。

注意：

一条路径指的是两个城市之间的道路序列。
一条路径可以多次包含同一条道路，你也可以沿着路径多次到达城市 1 和城市 n 。
测试数据保证城市 1 和城市n 之间至少有一条路径。

示例 1：

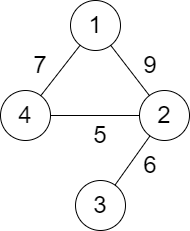
输入：n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出：5
解释：城市 1 到城市 4 的路径中，分数最小的一条为：1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。

示例 2：

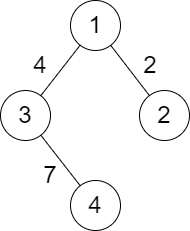
输入：n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出：2
解释：城市 1 到城市 4 分数最小的路径是：1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。

提示：

2 <= n <= 105
1 <= roads.length <= 105
roads[i].length == 3
1 <= ai, bi <= n
ai != bi
1 <= distancei <= 104
不会有重复的边。
城市 1 和城市 n 之间至少有一条路径。

地址

https://leetcode.cn/contest/weekly-contest-322/problems/minimum-score-of-a-path-between-two-cities/

题意

广度优先搜索

思路

题目出的很奇怪，由于题目求的所有路径中小的两点距离，且两点间的路径可以来回重复，这就变的非常简单的题目，我们直接找到包含节点 $1$ 与节点 $n-1$ 的所有在的有向图构成的连通单元，并找到该连通单元中最小的边的值即可。

我们可以用 $BFS$ 遍历所有的边即可。标记每个顶点，由于任意两个顶点中有且只有一条边连接，所有我们遍历所有的顶点即可遍历所有的边。

复杂度分析

时间复杂度：时间复杂度为 $O(V + E)$，$V$ 表示顶点个数，$E$ 表示边的个数。
空间复杂度：空间复杂度为 $O(V + E)$，$V$ 表示顶点个数，$E$ 表示边的个数。

代码

class Solution {
public:
    int minScore(int n, vector<vector<int>>& roads) {
        vector<vector<pair<int,int>>> graph(n);
        for (auto v : roads) {
            int x = v[0] - 1, y = v[1] - 1, cost = v[2];
            graph[x].emplace_back(y, cost);
            graph[y].emplace_back(x, cost);
        }
        int res = INT_MAX;
        vector<bool> visit(n, false);
        queue<int> qu;
        qu.emplace(0);
        visit[0] = true;
        while(!qu.empty()) {
            auto cur = qu.front();
            qu.pop();
            for (auto [next, cost] : graph[cur]) {
                res = min(res, cost);
                if (visit[next]) {
                    continue;
                }
                qu.emplace(next);
                visit[next] = true;
            }
        }
        return res;
    }
};

6256. 将节点分成尽可能多的组

给你一个正整数 n ，表示一个无向图中的节点数目，节点编号从 1 到 n 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条双向边。注意给定的图可能是不连通的。

请你将图划分为 m 个组（编号从 1 开始），满足以下要求：

图中每个节点都只属于一个组。
图中每条边连接的两个点 [ai, bi] ，如果 ai 属于编号为 x 的组，bi 属于编号为 y 的组，那么 |y - x| = 1 。

请你返回最多可以将节点分为多少个组（也就是最大的 m ）。如果没办法在给定条件下分组，请你返回 -1 。

示例 1：

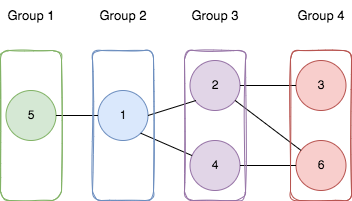
输入：n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
输出：4
解释：如上图所示，
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组，将第三个组或者第四个组中任何一个节点放到第五个组，至少有一条边连接的两个节点所属的组编号不符合题目要求。

示例 2：

输入：n = 3, edges = [[1,2],[2,3],[3,1]]
输出：-1
解释：如果我们将节点 1 放入第一个组，节点 2 放入第二个组，节点 3 放入第三个组，前两条边满足题目要求，但第三条边不满足题目要求。
没有任何符合题目要求的分组方式。

提示：

1 <= n <= 500
1 <= edges.length <= 104
edges[i].length == 2
1 <= ai, bi <= n
ai != bi
两个点之间至多只有一条边。

地址

https://leetcode.cn/contest/weekly-contest-322/problems/divide-nodes-into-the-maximum-number-of-groups/

题意

动态规划

思路

首先根据题目的思路大概就可以知道本体的时间复杂度范围大概在 $V\times (V + E)$ 内可以接受，因为本题中 $0 \le V \le 500$。
对于每个连通图单元的分组我们观察一下一定有以下特这：

一定包含只有一个节点的分组，否则一定存在属于某条边的两个节点被分到一个分组中，这样就部分题目要求满足 $|x-y| = 1$。
我们一旦确定某个分组，则根据依赖关系可知，其他分组也可以确定，此时我们即可计算出分组的个数；
我们依次枚举只含有一个节点的分组，即可得到该连通单元的最大分组；
不同连通单元之间的最大分组互不影响；
根据上述的分析可以知道，解题步骤如下：
首先求出图中各个连通单元 $component$，此时我们可以用 $BFS$ 求出即可；
其次我们可以依次对每个 $component$ 求出最大分组：
- 我们依次枚举 $component$ 中的顶点 $V_{i}$ 作为分组的起点，然后依次求出其他所有可能的分组，我们对分组进行编号 $order[v_{i}]$，我们知道同属于一条边的两个节点 $x,y$，则此时一定满足 $|order[x] -order[y]| = 1$；
- 依据上述条件作为检测依据，检查该 $component$ 可被完成划分，最得到最大的分组 $cnt$；
所有节点的最大划分即为 $cnt_{j}$ 之和。

复杂度分析：

时间复杂度：$O(V \times (V + E))$，其中 $V$ 表示顶点的个数，$E$ 表示边的数组。
空间复杂度：$O(V + E)$，其中 $V$ 表示顶点的个数，$E$ 表示边的数组。

代码

class Solution {
public:
    int magnificentSets(int n, vector<vector<int>>& edges) {
        vector<vector<int>> adj(n);
        for (auto v : edges) {
            int x = v[0] - 1, y = v[1] - 1;
            adj[x].emplace_back(y);
            adj[y].emplace_back(x);
        }
        
        int ans = 0;
        vector<bool> visit(n, false);
        for (int i = 0; i < n; i++) {
            if (!visit[i]) {
                vector<int> component;
                queue<int> qu;
                qu.emplace(i);
                visit[i] = true;
                while(!qu.empty()) {
                    int curr = qu.front();
                    qu.pop();
                    component.emplace_back(curr);
                    for (auto next : adj[curr]) {
                        if(visit[next]) continue;
                        visit[next] = true;
                        qu.emplace(next);
                    }
                }
                
                int cnt = -1;
                for (auto v : component) {
                    queue<int> qu;
                    vector<int> order(n, -1);
                    qu.emplace(v);
                    order[v] = 0;
                    int step = 0;
                    bool valid = true;
                    while(!qu.empty() && valid) {
                        int sz = qu.size();
                        step++;
                        for (int j = 0; j < sz; j++) {
                            int curr = qu.front();
                            qu.pop();
                            for (auto next : adj[curr]) {
                                if (order[next] >= 0) {
                                    if (abs(order[curr] - order[next]) != 1) {
                                        valid = false;
                                        break;
                                    }
                                    continue;
                                }
                                order[next] = step;
                                qu.emplace(next);
                            }
                        }
                    }
                    if (valid) {
                        cnt = max(cnt, step);
                    }
                }
                if (cnt < 0) {
                    return -1;
                }
                ans += cnt;
            }            
        }
        return ans;
    }
};

欢迎关注和打赏，感谢支持！

关注我的博客: http://whistle-wind.com/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: 力扣周赛题解

← leetcode contest 321 leetcode contest 323 →

扫描二维码，分享此文章