leetcode biweekly contest 92
前三题确实是太简单了,最后一题稍微有点奥数的思想。
6249. 分割圆的最少切割次数
圆内一个 有效切割 ,符合以下二者之一:
- 该切割是两个端点在圆上的线段,且该线段经过圆心。
- 该切割是一端在圆心另一端在圆上的线段。
一些有效和无效的切割如下图所示。
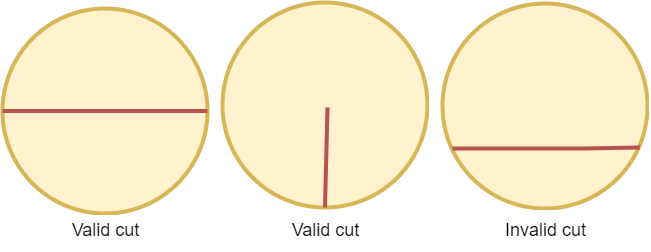
给你一个整数 n ,请你返回将圆切割成相等的 n 等分的 最少 切割次数。
示例 1:
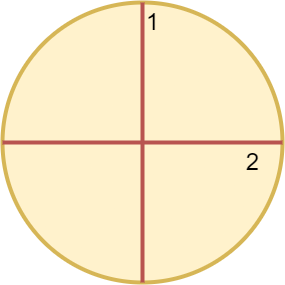
输入:n = 4 |
示例 2:
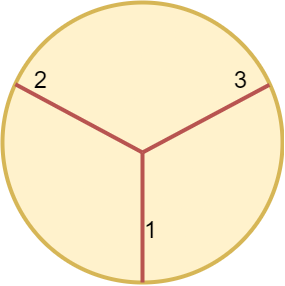
输入:n = 3 |
提示:
1 <= n <= 100
地址
https://leetcode.cn/contest/biweekly-contest-92/problems/minimum-cuts-to-divide-a-circle/
题意
数学
思路
- 对称性的问题,如果 $n$ 能被 $2$ 整除,此时我们可以先从中切一次,将园等分为两部分,剩余的等分则刚好两遍半圆的等分次数相等即可,因此当 $n$ 为偶数时此时需要的最少此时为 $\dfrac{n}{2}$,否则为 $n$。特殊情况需要考虑,当 $n= 1$时,此时不需要任何切分。
- 复杂度分析:
- 时间复杂度:$O(1)$。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6277. 行和列中一和零的差值
给你一个下标从 0 开始的 m x n 二进制矩阵 grid 。
我们按照如下过程,定义一个下标从 0 开始的 m x n 差值矩阵 diff :
- 令第
i行一的数目为onesRowi。 - 令第
j列一的数目为onesColj。 - 令第
i行零的数目为zerosRowi。 - 令第
j列零的数目为zerosColj。 diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj
请你返回差值矩阵 diff 。
示例 1:
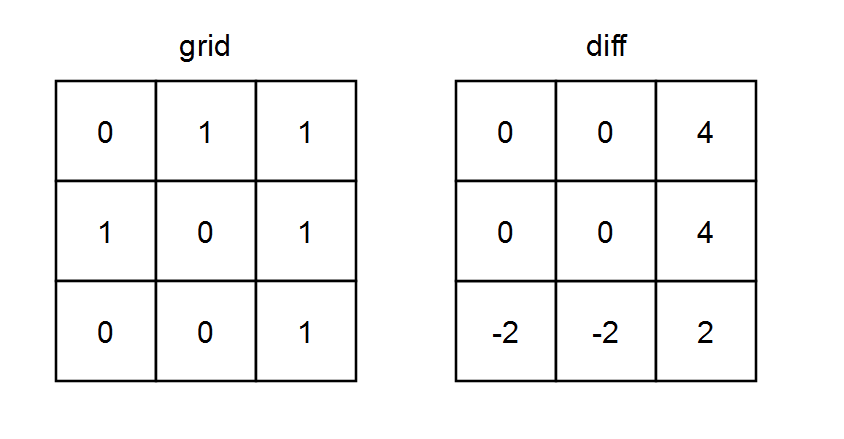
输入:grid = [[0,1,1],[1,0,1],[0,0,1]] |
示例 2:
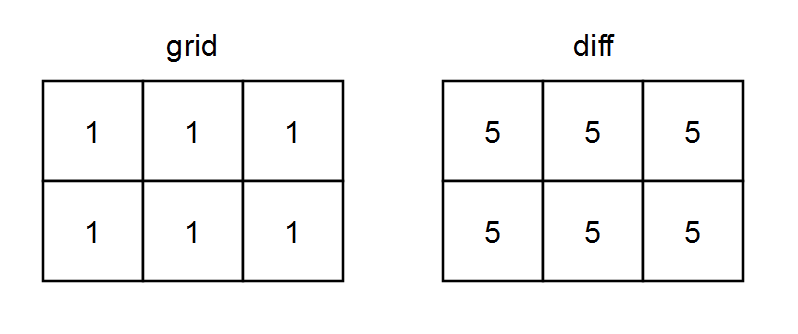
输入:grid = [[1,1,1],[1,1,1]] |
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 105grid[i][j]要么是0,要么是1。
地址
题意
直接模拟
思路
- 直接模拟即可,我们求出每一行与每一列中 $1$ 的个即可,然后按照题目要求进行模拟即可。
$$
res[i][j] = 2 * onesRow[i] + 2 * onesCol[j] - m - n
$$ - 复杂度分析:
- 时间复杂度:$O(m\times n)$,其中 $m,n$ 为矩阵的行数与列数。
- 空间复杂度:$O(m + n)$,其中 $m,n$ 为矩阵的行数与列数。
代码
class Solution { |
6250. 商店的最少代价
给你一个顾客访问商店的日志,用一个下标从 0 开始且只包含字符 'N' 和 'Y' 的字符串 customers 表示:
- 如果第
i个字符是'Y',它表示第i小时有顾客到达。 - 如果第
i个字符是'N',它表示第i小时没有顾客到达。
如果商店在第 j 小时关门(0 <= j <= n),代价按如下方式计算:
- 在开门期间,如果某一个小时没有顾客到达,代价增加
1。 - 在关门期间,如果某一个小时有顾客到达,代价增加
1。
请你返回在确保代价 最小 的前提下,商店的 最早 关门时间。
注意,商店在第 j 小时关门表示在第 j 小时以及之后商店处于关门状态。
示例 1:
输入:customers = "YYNY" |
示例 2:
输入:customers = "NNNNN" |
示例 3:
输入:customers = "YYYY" |
提示:
1 <= customers.length <= 105customers只包含字符'Y'和'N'。
地址
https://leetcode.cn/contest/biweekly-contest-92/problems/minimum-penalty-for-a-shop/
题意
滑动窗口
思路
- 我们设商店营业到小时 $i$ 的开门代价为 $cost_1[i]$,我们设商店从小时 $i$ 开始关门的关门代价为 $cost_2[i]$。我们知道当商店从 $i$ 开始关门的总代价为 $cost[i] = cost_1[i-1] + cost_2[i]$,我们找到最小的 $cost$ 即可,本质为一个前缀和的问题,可以将空间复杂度优化到 $O(1)$
- 复杂度分析
- 时间复杂度:时间复杂度为 $O(n)$,$n$ 数组的长度。
- 空间复杂度:空间复杂度为 $O(1)$ 。
代码
class Solution { |
6251. 统计回文子序列数目
给你数字字符串 s ,请你返回 s 中长度为 5 的 回文子序列 数目。由于答案可能很大,请你将答案对 109 + 7 取余 后返回。
提示:
- 如果一个字符串从前往后和从后往前读相同,那么它是 回文字符串 。
- 子序列是一个字符串中删除若干个字符后,不改变字符顺序,剩余字符构成的字符串。
示例 1:
输入:s = "103301" |
示例 2:
输入:s = "0000000" |
示例 3:
输入:s = "9999900000" |
提示:
1 <= s.length <= 104s只包含数字字符。
地址
https://leetcode.cn/contest/biweekly-contest-92/problems/count-palindromic-subsequences/
题意
动态规划
思路
- 典型的动态规划,重点在于题目的提示如下:
- 回文字符串的长度为 $5$;
- 字符串中只包含数字;
- 枚举每个字符作为回文字符串中心,则左右两遍的字符串的范围为 $\text{00}-\text{99}$,此时最多只有 $100$ 种可能,因此我们只需要统计以每个字符串左右两遍能构成字符串 $x, x \in [0,99]$ 的数目即可。此时我们可以利用动态规划:
- 设 $dp_1[i][j]$ 表示前 $i$ 个字符中含有的字符 $j$ 的数目,$dp_2[i][a\times 10 + b]$ 表示前 $i$ 个字符中含有的形成的字符串 $\text{ab}$ 的数目,则此时我们可以得到递推公式:
$$
dp_1[i][j] = dp_1[i-1][j] + 1 \quad if \quad nums[i] = j \
dp_1[i][j] = dp_1[i-1][j] \quad if \quad nums[i] \neq j \
dp_2[i][a\times 10 + b] = dp_2[i-1][a\times 10 + b] + dp_2[i-1][a] \quad if \quad nums[i] = b \
dp_2[i][a\times 10 + b] = dp_2[i-1][a\times 10 + b]\quad if \quad nums[i] \neq b \
$$
非常容易理解的动态规划即可求的左右两遍构成字符串 $x$ 的数目,设 $l(i-1, x)$ 表示从 $i$ 的左边构成字符串 $x$ 的数目,设 $r(i-1, x)$ 表示从 $i$ 的右边边构成字符串 $x$ 的数目,则此时我们可以得到递推公式如下:
$$
tot = \sum_{i=2}^{n-3}\sum_{j = 0}^{99}l(i-1,j) \times r(i+1,j)
$$
3. 复杂度分析:
- 时间复杂度:$O(n \times |\Sigma|^2)$,其中 $n$ 表示给定的字符串的长度, $|\Sigma|$ 表示给定的字符集的大小,在这里字符集为数字,此时 $|\Sigma| = 10$。
- 空间复杂度:$O(n \times |\Sigma|^2)$,其中 $n$ 表示给定的字符串的长度, $|\Sigma|$ 表示给定的字符集的大小,在这里字符集为数字,此时 $|\Sigma| = 10$。
代码
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://whistle-wind.com/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
