且听疯吟

leetcode contest 319

2022-11-25

leetcode contest 319

周赛又是手速场的一次，感觉题目都太简单了。

6233. 温度转换

给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度，以 摄氏度（Celsius）为单位。

你需要将摄氏度转换为 开氏度（Kelvin）和 华氏度（Fahrenheit），并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。

返回数组 ans 。与实际答案误差不超过 10-5 的会视为正确答案。

注意：

  • 开氏度 = 摄氏度 + 273.15
  • 华氏度 = 摄氏度 * 1.80 + 32.00

示例 1 ：

输入：celsius = 36.50
输出：[309.65000,97.70000]
解释：36.50 摄氏度：转换为开氏度是 309.65 ，转换为华氏度是 97.70 。

示例 2 ：

输入：celsius = 122.11
输出：[395.26000,251.79800]
解释：122.11 摄氏度：转换为开氏度是 395.26 ，转换为华氏度是 251.798 。

提示：

  • 0 <= celsius <= 1000

地址

https://leetcode.cn/contest/weekly-contest-319/problems/convert-the-temperature/

题意

直接模拟

思路

  1. 直接模拟计算温度即可。
  2. 复杂度分析：
  • 时间复杂度：$O(1)$。
  • 空间复杂度：$O(1)$。

代码

class Solution {
public:
    vector<double> convertTemperature(double celsius) {
        vector<double> res(2);
        res[0] = celsius + 273.15;
        res[1] = celsius * 1.80 + 32.00;
        return res;
    }
};

6234. 最小公倍数为 K 的子数组数目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。

子数组 是数组中一个连续非空的元素序列。

数组的最小公倍数 是可被所有数组元素整除的最小正整数。

示例 1 ：

输入：nums = [3,6,2,7,1], k = 6
输出：4
解释：以 6 为最小公倍数的子数组是：
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]
- [3,6,2,7,1]

示例 2 ：

输入：nums = [3], k = 2
输出：0
解释：不存在以 2 为最小公倍数的子数组。

提示：

  • 1 <= nums.length <= 1000
  • 1 <= nums[i], k <= 1000

地址

https://leetcode.cn/contest/weekly-contest-319/problems/number-of-subarrays-with-lcm-equal-to-k/

题意

数学问题

思路

  1. 由于题目给定的数量很小，所有就非常简单了，直接暴力检测所有可能的子数组，如果满足它们的最小公倍数为 $k$ 则返回即可。
  2. 检测时可以进行减枝，如果当前的数不能被 $k$ 整除直接返回即可。
  3. 复杂度分析：
  • 时间复杂度：时间复杂度为 $O(n)$。
  • 空间复杂度：空间复杂度为 $O(1)$。

代码

class Solution {
public:
    int subarrayLCM(vector<int>& nums, int k) {
        int n = nums.size();
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int x = nums[i];
            for (int j = i; j < n; j++) {
                if (k % nums[j] == 0) {
                    x = x * nums[j] / __gcd(x, nums[j]);
                    if (x == k) {
                        ans++;
                    }
                } else {
                    break;
                }
            }
        }
        return ans;
    }
};

6235. 逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

img

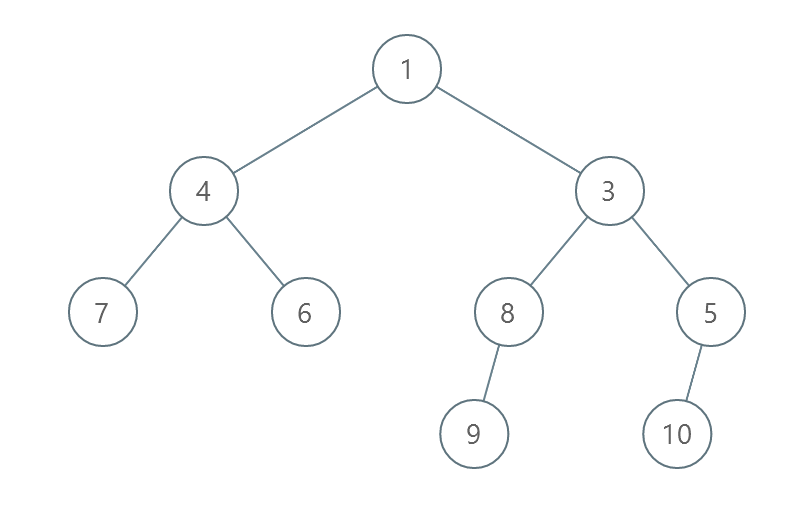
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

示例 2 ：

img

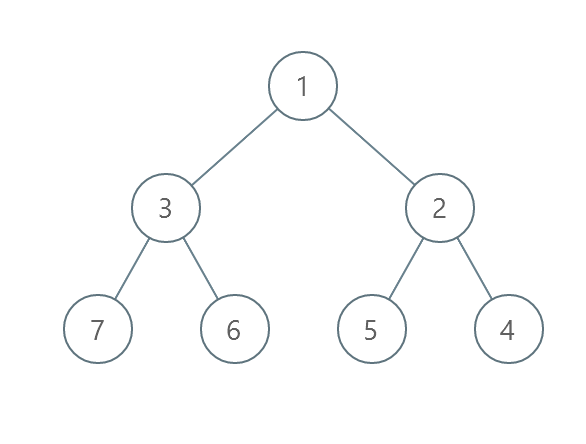
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：
- 交换 3 和 2 。第 2 层变为 [2,3] 。 
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。 
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作，所以返回 3 。 
可以证明 3 是需要的最少操作数目。

示例 3 ：

img

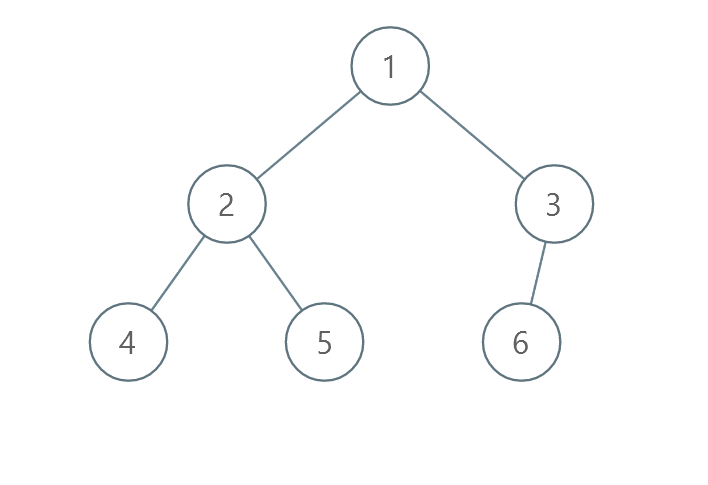
输入：root = [1,2,3,4,5,6]
输出：0
解释：每一层已经按递增顺序排序，所以返回 0 。

提示：

  • 树中节点的数目在范围 [1, 105] 。
  • 1 <= Node.val <= 105
  • 树中的所有值 互不相同 。

地址

https://leetcode.cn/contest/weekly-contest-319/problems/minimum-number-of-operations-to-sort-a-binary-tree-by-level/

题意

树的层次遍历

思路

  1. 由于每次交换不涉及到交换子树，只涉及到交换节点值，所以我们直接按照层次遍历，然后求出每层的最小交换次数即可。
  2. 求一个数组最小的交换次数为经典问题，即将一个数组变为有序的最少交换次数，可以有两种方法：
  • 找到图中环的最大数目，在这里由于题目中所有的元素都不相等，所有一个元素只能属于一个环，直接利用 dfs 求出所有的环即可。
  • 贪心策略，直接进行交换即可，直到元素无法完成交换为止，这是由于我们题目中的所有元素均不相等，所以最优的交换策略时唯一的。
  • 可以参考解法：Minimum number of swaps required to sort an array，如果元素可以重复则情况比较复杂的多。
  1. 复杂度分析
  • 时间复杂度：时间复杂度为 $O(n \log n)$，$n$ 为给定的节点的数目。
  • 空间复杂度：空间复杂度为 $O(n)$，$n$ 为给定的节点的数目。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getMinSwaps(vector<int> &nums){
        //排序
        vector<int> nums1(nums);
        sort(nums1.begin(),nums1.end());
        unordered_map<int,int> m;
        int len = nums.size();
        for (int i = 0; i < len; i++){
            m[nums1[i]] = i;//建立每个元素与其应放位置的映射关系
        }
        int loops = 0;//循环节个数
        vector<bool> flag(len,false);
        //找出循环节的个数
        for (int i = 0; i < len; i++){
            if (!flag[i]){//已经访问过的位置不再访问
                int j = i;
                while (!flag[j]){
                    flag[j] = true;
                    j = m[nums[j]];//原序列中j位置的元素在有序序列中的位置
                }
                loops++;
            }
        }
        return len - loops;
    }
    
    int minimumOperations(TreeNode* root) {
        queue<TreeNode *> qu;
        qu.emplace(root);
        int res = 0;
        while (!qu.empty()) {
            int sz = qu.size();
            vector<int> arr;
            for (int i = 0; i < sz; i++) {
                TreeNode *node = qu.front();
                qu.pop();
                arr.emplace_back(node->val);
                if (node->left) {
                    qu.emplace(node->left);
                }
                if (node->right) {
                    qu.emplace(node->right);
                }
            }
            res += getMinSwaps(arr);
        }
        return res;
    }
};

6236. 不重叠回文子字符串的最大数目

给你一个字符串 s 和一个 正 整数 k 。

从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串：

  • 每个子字符串的长度 至少 为 k 。
  • 每个子字符串是一个 回文串 。

返回最优方案中能选择的子字符串的 最大 数目。

子字符串 是字符串中一个连续的字符序列。

示例 1 ：

输入：s = "abaccdbbd", k = 3
输出：2
解释：可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文，且长度至少为 k = 3 。
可以证明，无法选出两个以上的有效子字符串。

示例 2 ：

输入：s = "adbcda", k = 2
输出：0
解释：字符串中不存在长度至少为 2 的回文子字符串。

提示：

  • 1 <= k <= s.length <= 2000
  • s 仅由小写英文字母组成

地址

https://leetcode.cn/contest/weekly-contest-319/problems/maximum-number-of-non-overlapping-palindrome-substrings/

题意

动态规划

思路

  1. 第四题为简单的动态规划题目了，太常见的题目了，设 $dp[i]$ 表示前 $i$ 个字符构成的回文串的最大数目，$valid[i][j]$ 表示字符串从 $i$ 到 $j$ 是否为回文字符串，则可以知道递推关系如下:
    $$
    dp[i] = \max(dp[i], dp[i-j] + valid[i-j+1][i]) \quad j \ge k
    $$
  2. 首先我们求出 $s[i,\cdots,j]$ 是否为回文字符串，我们每次以 $i$ 为中心向左右扩展即可。然后利用上述的递推关系求出即可。
  3. 复杂度分析：
  • 时间复杂度：$O(n^2)$，其中 $n$ 表示给定的字符串的长度。
  • 空间复杂度：$O(n^2)$，其中 $n$ 表示给定的字符串的长度。

代码

class Solution {
public:
    int maxPalindromes(string s, int k) {
        int n = s.size();
        vector<vector<bool>> valid(n, vector<bool>(n, false));
        for (int i = 0; i < n; i++) {
            valid[i][i] = true;
            for (int l = i, r = i; l >= 0 && r < n && s[l] == s[r]; l--, r++) {
                valid[l][r] = true;
            }
            for (int l = i, r = i + 1; l >= 0 && r < n && s[l] == s[r]; l--, r++) {
                valid[l][r] = true;
            }
        }
        vector<int> dp(n + 1, 0);
        for (int i = 1; i <= n; i++) {
            dp[i] = dp[i - 1];
            for (int j = i - k; j >= 0; j--) {
                if (valid[j][i - 1]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[n];
    }
};

欢迎关注和打赏，感谢支持！

Tags: 力扣周赛
← leetcode contest 320 leetcode biweekly contest 92 →

扫描二维码，分享此文章