leetcode weekly contest 318
第四题稍微复杂的动态规划,总的来说难度还可以接受。
6229. 对数组执行操作
题目
给你一个下标从 0 开始的数组 nums ,数组大小为 n ,且由 非负 整数组成。
你需要对数组执行 n - 1 步操作,其中第 i 步操作(从 0 开始计数)要求对 nums 中第 i 个元素执行下述指令:
- 如果
nums[i] == nums[i + 1],则nums[i]的值变成原来的2倍,nums[i + 1]的值变成0。否则,跳过这步操作。
在执行完 全部 操作后,将所有 0 移动 到数组的 末尾 。
- 例如,数组
[1,0,2,0,0,1]将所有0移动到末尾后变为[1,2,1,0,0,0]。
返回结果数组。
注意 操作应当 依次有序 执行,而不是一次性全部执行。
示例 1:
输入:nums = [1,2,2,1,1,0] |
示例 2:
输入:nums = [0,1] |
提示:
2 <= nums.length <= 20000 <= nums[i] <= 1000
地址
https://leetcode.cn/contest/weekly-contest-318/problems/apply-operations-to-an-array/
题意
直接模拟
思路
- 简单题目直接模拟即可,对于前后相等的元素将前面的元素变为原来的 $2$ 倍,同时将后一个元素设置为 $0$,之后再进行移动即可。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(1)$。
代码
class Solution { |
6230. 长度为 K 子数组中的最大和题目
题目
给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和:
- 子数组的长度是
k,且 - 子数组中的所有元素 各不相同 。
返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件,返回 0 。
子数组 是数组中一段连续非空的元素序列。
示例 1:
输入:nums = [1,5,4,2,9,9,9], k = 3 |
示例 2:
输入:nums = [4,4,4], k = 3 |
提示:
1 <= k <= nums.length <= 1051 <= nums[i] <= 105
地址
题意
哈希统计
思路
- 我们用哈希表统计连续的 $k$ 个元素,并同时记录 $k$ 个元素的和,如果哈希表中不同的元素刚好等于 $k$ 个,则表示当前的连续子数组符合题目要求,否则则不符合,同时我们将最左端的元素移除,然后继续遍历下一个元素。。
- 复杂度分析:
- 时间复杂度:时间复杂度为 $O(n)$,$n$ 表示数组的长度。
- 空间复杂度:时间复杂度为 $O(n)$,$n$ 表示数组的长度。
代码
class Solution { |
6231. 雇佣 K 位工人的总代价
题目
给你一个下标从 0 开始的整数数组 costs ,其中 costs[i] 是雇佣第 i 位工人的代价。
同时给你两个整数 k 和 candidates 。我们想根据以下规则恰好雇佣 k 位工人:
总共进行
k轮雇佣,且每一轮恰好雇佣一位工人。在每一轮雇佣中,从最前面
candidates
和最后面
candidates
人中选出代价最小的一位工人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。
- 比方说,
costs = [3,2,7,7,1,2]且candidates = 2,第一轮雇佣中,我们选择第4位工人,因为他的代价最小[*3,2*,7,7,***1**,2*]。 - 第二轮雇佣,我们选择第
1位工人,因为他们的代价与第4位工人一样都是最小代价,而且下标更小,[*3,**2***,7,*7,2*]。注意每一轮雇佣后,剩余工人的下标可能会发生变化。
- 比方说,
如果剩余员工数目不足
candidates人,那么下一轮雇佣他们中代价最小的一人,如果有多位代价相同且最小的工人,选择下标更小的一位工人。一位工人只能被选择一次。
返回雇佣恰好 k 位工人的总代价。
示例 1:
输入:costs = [17,12,10,2,7,2,11,20,8], k = 3, candidates = 4 |
示例 2:
输入:costs = [1,2,4,1], k = 3, candidates = 3 |
提示:
1 <= costs.length <= 1051 <= costs[i] <= 1051 <= k, candidates <= costs.length
地址
https://leetcode.cn/contest/weekly-contest-318/problems/total-cost-to-hire-k-workers/
题意
堆
思路
- 我们分别记录当前已经进入候选队列的左侧的终点索引为 $l$, 右侧进入候选队列的终点为 $r$,初始化时我们将 $[0,\cdots,candidates-1],[n-candidates, \cdots,n-1]$ 中的所有优先队列,并标记进入队列的数是左侧的部分还是右侧的部分。
- 每次从队列中取出最小的数,如果取出的数是左边的待选序列,则我们再从数组的左侧取一个值进入到队列中,此时令 $l = l + 1$;如果取出的数是右边的待选序列,则我们再从数组的右侧取一个值进入到队列中,此时令 $r = r - 1$。直到满足 $l = r - 1$ 为止,此时数组中的所有元素都已压入到待选序列中。
- 复杂度分析:
- 时间复杂度:时间复杂度为 $O(k \log n )$,$n$ 为数组的元素,$k$ 为给定的选择次数。
- 空间复杂度:空间复杂度为 $O(n)$,$n$ 为数组的元素。
代码
class Solution { |
6232. 最小移动总距离
题目
X 轴上有一些机器人和工厂。给你一个整数数组 robot ,其中 robot[i] 是第 i 个机器人的位置。再给你一个二维整数数组 factory ,其中 factory[j] = [positionj, limitj] ,表示第 j 个工厂的位置在 positionj ,且第 j 个工厂最多可以修理 limitj 个机器人。
每个机器人所在的位置 互不相同 。每个工厂所在的位置也 互不相同 。注意一个机器人可能一开始跟一个工厂在 相同的位置 。
所有机器人一开始都是坏的,他们会沿着设定的方向一直移动。设定的方向要么是 X 轴的正方向,要么是 X 轴的负方向。当一个机器人经过一个没达到上限的工厂时,这个工厂会维修这个机器人,且机器人停止移动。
任何时刻,你都可以设置 部分 机器人的移动方向。你的目标是最小化所有机器人总的移动距离。
请你返回所有机器人移动的最小总距离。测试数据保证所有机器人都可以被维修。
注意:
- 所有机器人移动速度相同。
- 如果两个机器人移动方向相同,它们永远不会碰撞。
- 如果两个机器人迎面相遇,它们也不会碰撞,它们彼此之间会擦肩而过。
- 如果一个机器人经过了一个已经达到上限的工厂,机器人会当作工厂不存在,继续移动。
- 机器人从位置
x到位置y的移动距离为|y - x|。
示例 1:
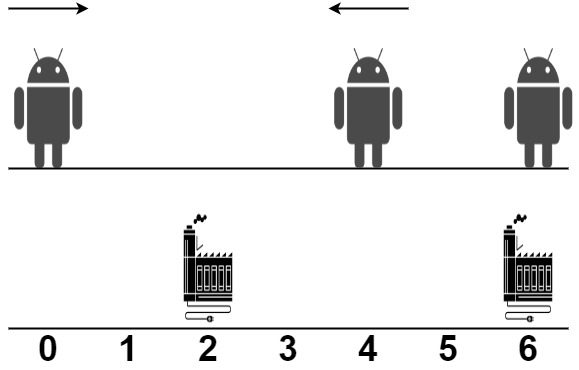
输入:robot = [0,4,6], factory = [[2,2],[6,2]] |
示例 2:
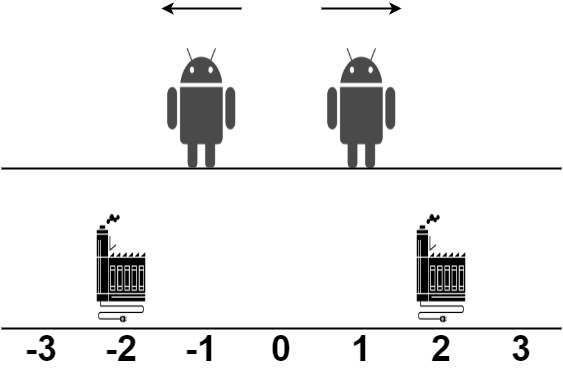
输入:robot = [1,-1], factory = [[-2,1],[2,1]] |
提示:
1 <= robot.length, factory.length <= 100factory[j].length == 2-109 <= robot[i], positionj <= 1090 <= limitj <= robot.length- 测试数据保证所有机器人都可以被维修。
地址
https://leetcode.cn/contest/weekly-contest-318/problems/minimum-total-distance-traveled/
题意
动态规划
思路
- 设 $dp[i][j]$ 表示前 $i$ 个工厂维修前 $j$ 个机器人的最小距离之和。则我们可以知道相关的递推公式如下:
$$
dp[i][j] = \min\limits_{k=0}^{\min(j, limit[i])} (dp[i-1][j - k] + \sum_{s=1}^{k}|robot[j-s]-postion[i]|)
$$
题目主要的难点在于最后一个工厂可以修理 $[0,\min(limit[i],m)]$ 个机器人。前 $i$ 个工厂的维修总数目为 $j$,如果最后一个工厂 $i$ 的维修数目依次为 $k$,则前 $i-1$ 个工厂的维修数目为 $j-k$,我们依次尝试工厂 $i$ 可能的数目即可得到递推公式。
2 . 复杂度分析:
- 时间复杂度:$O(m^2 \times n)$,其中 $m$ 表示机器人的数目,$n$ 表示工厂的数目。
- 空间复杂度:$O(m^2 \times n)$,其中 $m$ 表示机器人的数目,$n$ 表示工厂的数目。
代码
class Solution { |
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://mikemeng.org/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
